Question 857715: Solve cos 2 θ = cos θ + 2 for 0 < θ < 2p
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i'll use x instead of theta.
your problem is:
cos(2x) = cos(x) + 2 for 0 < x < 2pi
you can graph these equations and find the intersect and that would tell you what the value is.
that's cheating though because it's too easy, assuming you have a graphing calculator handy and know how to use it.
it does make for a fascinating graph though, as can be seen below:

those intersection points look like they will be at -pi and + pi.
but cheating isn't allowed, so we have to figure this out algebraically, or trigonometrically, however they wish to call it.
start with:
cos(2x) = cos(x) + 2 for 0 < x < 2pi
the double angle formula tells you that:
cos(2x) = cos^2(x) - sin^2(x)
replace cos(2x) with cos^2(x) - sin^2(x) and your equation becomes:
cos^2(x) - sin^2(x) = cos(x) + 2
from the basic identify of sin^2(x) + cos^2(x) = 1, you can solve for sin^2(x) to get:
sin^2(x) = 1 - cos^2(x)
you can replace sin^2(x) in your equation with 1 - cos^2(x) to get:
cos^2(x) - (1 - cos^2(x) = cos(x) + 2
simplify this to get:
cos^2(x) - 1 + cos^2(x) = cos(x) + 2
simplify further to get:
2cos^2(x) - 1 = cos(x) + 2
subtract cos(x) and subtract 2 from both sides of this equation to get:
2cos^2(x) - 1 - cos(x) - 2 = 0
simplify to get:
2cos^2(x) - cos(x) - 3 = 0
this is a quadratic equation that can be factored.
start with:
2cos^2(x) - cos(x) - 3 = 0
factor to get:
(2cos(x) - 3) * (cos(x) + 1) = 0
set each of these factors equal to 0 to get:
2cos(x) - 3) = 0 and cos(x) + 1) = 0
solve for cos(x) to get:
cos(x) = 3/2 and cos(x) = -1
since cos(x) cannot be greater than 1, cos(x) = 3/2 is not a valid solution, therefore extraneous.
the only valid solution is:
cos(x) = -1
cos(x) = -1 when x = 180 degrees or when x = pi radians.
radians = degrees * pi / 180
degrees = radians * 180 / pi
you are interested in solutions between the values of x = 0 to x = 2*pi.
it appears that cos(x) = -1 at only one location between x = 0 and x = 2*pi, and that is when x = pi.
at x = pi, cos(2x) is equal to 1 because 2x = 360 degrees which is the same as 0 degrees and cos(0) = 1.
that's what makes the graph interesting.
cos(x) + 2 is at a minimum point on its graph and cos(2x) is at a maximum point on its graph. the minimum point of cos(x) + 2 is equal to 1 and the maximum point of cos(2x) is also equal to 1 and so they intersect when x = 180 degrees or when x = pi radians which is the same value of x
the graph is displayed again below for your convenience, with the interval changed to go from 0 to 2*pi rather than from -2pi to 2pi in order to be consistent with the interval stated in the problem.
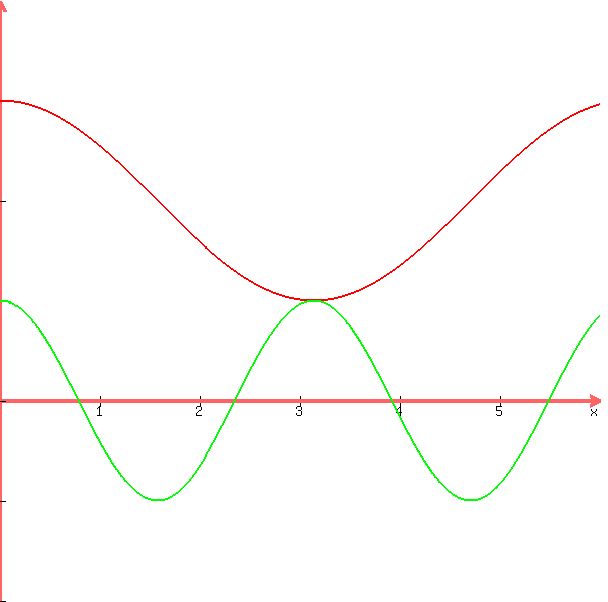
as you can see, there is only one value of x where the graphs of both equations intersect in the interval from 0 to 2pi if you are dealing in radians, and in the interval of 0 to 360 degrees if you are dealing in degrees.
there are lots of websites that contain references to trigonometric identities.
the following website is just one of them.
http://www.clarku.edu/~djoyce/trig/identities.html
|
|
|