The angle must be located in the 2nd quadrant. In the second quadrant: sin and csc are positive, while cos, sec, tan, and cot are negative.
tan(t) = 8. tan = opp/adj. Pick any numbers for opp/adj such that the quotient is 8. Don't worry about the sign of your answers. The quadrant (2nd) tells you the sign of each of the functions.
tan(t)= 8 = 8/1. Opposite side is 8, adjacent side is 1. The hypotenuse is 
Now you can find all of the requested values. Remember, only sin and csc are positive:
sin(t) = opp/hyp = 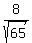 = approximately .992
= approximately .992
csc(t) = 1/(sin(t) = 1/.992 = approximately 1.008
cos(t) = adj/hyp = 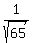 = appox. -.124. Remember, cos is negative in the second quadrant. Don't worry about the sign, until you complete the calculation. Then add the sign based on the quadrant.
= appox. -.124. Remember, cos is negative in the second quadrant. Don't worry about the sign, until you complete the calculation. Then add the sign based on the quadrant.
sec(t) = 1/cos(t) = 1/(-.124) = appox. -8.062.
tan(t) is already given: -8. cot(t) is 1/tan(t) = -1/8