Question 807759: How can I find the arccos of 1, with all possible answers?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! ANSWER:
The function   is defined as the angle is defined as the angle  that satisfies that satisfies  and and 
(and we measure angles in radians, not degrees).
If the question is finding the angle  such that such that  , ,
then there are infinite answers,
so you have to give them as  in radians, in radians,
(or  if you measure angles in degrees), if you measure angles in degrees),
where  is any integer. is any integer.
However, to define   as a function, as a function,
we choose just the most trivial of those answers,  , ,
so   (just one answer). (just one answer).
EXPLANATION AND MORE:
The drawing below shows the unit circle and an angle,  , in standard position. , in standard position.
  or or  depending on the units you use for angles. depending on the units you use for angles.
Angles are measured as turns counterclockwise from ray OA to ray OB.
It is a useful way to define angles for technical issues,
such as stating the angle a control knob has to be turned to get to the desired position.
You start with OB coinciding with OA and  . .
As you turn OB around O, you eventually go one full turn and get back to OA,
and that turn is considered to be  or or  . .
After another turn, the angle would be 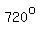 or or 
I say that the angle  in my drawing is in my drawing is  , ,
because I say that I just turned from OA to OB the shortest possible way.
If I said that I turned a little over 2 turns clockwise on my way from OA to OB, then it would be

Cosine is defined as the x-coordinate of point B, while sine is the y-coordinate.
In my drawing, those coordinates are
 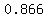 and and
 . .
There is another point in the circle (point C) with the same x-coordinate,
as there is another point (point D) with the same y-coordinate.
It is obvious that the only point in the circle with  is point A, is point A,
so for  we get infinite answers, but just one answer per turn, we get infinite answers, but just one answer per turn,
and the answers are all  or or  apart. apart.
The same thing happens for  and and  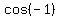 at the other extreme of the range of at the other extreme of the range of  values for the circle. values for the circle.
For values in between those extremes, such as
 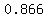 , ,
there are twice as many answers,
because there are twice as many points with that x-coordinate.
 so so 
and we can say  or or  if we choose the simplest way to define those angles. if we choose the simplest way to define those angles.
For the infinite answers to  , ,
we have to express all the coterminal angles (that differ from AOB and AOC by a whole number of turns) as
 (or (or  if we use degrees) for any integer if we use degrees) for any integer  . .
|
|
|