Question 77922: find all solutions for equation with value of x between 0 and 360 degrees:
1. sin(4x) + sin x = 0
I have 2(2sin(x) cos (x))(cox(2x)) + sin x = 0
so far but don't know which identity to use for cos(2x) that will help solve.
This is from my daughter's textbook but I don't have the book with me now. She's taking pre-calc in high school. Thanks
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!  Start with the given expression Start with the given expression
 Rewrite Rewrite 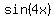 into into 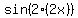
 Use the identity: Use the identity: 
 Use the identity: Use the identity:  again again
 Use the identity: Use the identity: 
 Distribute Distribute 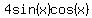
 Factor out a sin(x) Factor out a sin(x)
Since we know the value of x for  (the solution is x=0) we can ignore the sin(x) and try to solve the expression in the parenthesis (the solution is x=0) we can ignore the sin(x) and try to solve the expression in the parenthesis
 So lets focus on the terms in the parenthesis So lets focus on the terms in the parenthesis
Let 
So we get

 Rewrite -4y into -2y-2y. This will allow us to factor Rewrite -4y into -2y-2y. This will allow us to factor
 Group like terms and factor out the GCF Group like terms and factor out the GCF
 Factor Factor 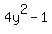 into into  using difference of squares using difference of squares
 Combine like terms (note: the common term is Combine like terms (note: the common term is 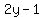 ) )
Now set each factor equal to zero. Lets start with 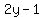



Now let  and solve for x note: I'm using radians and solve for x note: I'm using radians
 and and  Since our interval is [0,2pi] we must ignore the negative answer. So of these two answers, Since our interval is [0,2pi] we must ignore the negative answer. So of these two answers,  is the only solution. is the only solution.
Now let 
 Distribute the 2y Distribute the 2y
Use the quadratic formula to solve for y
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=20 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 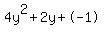 can be factored: can be factored:

Again, the answer is: 0.309016994374947, -0.809016994374947.
Here's your graph:
 |
So if we replace y with  we get these solutions we get these solutions
 or or 
Take the arccosine of both sides (for the solution  ) to solve for x ) to solve for x
 or or  Here are 2 more possible solutions. Since our interval is [0,2pi] we must ignore the negative answer. So of these two answers, Here are 2 more possible solutions. Since our interval is [0,2pi] we must ignore the negative answer. So of these two answers,  is the only solution. is the only solution.
Now lets use the other answer of 

Take the arccosine of both sides
 or or  Since our interval is [0,2pi] we must ignore the negative answer. So of these two answers, Since our interval is [0,2pi] we must ignore the negative answer. So of these two answers,  is the only solution. is the only solution.
-----------------------------------------------------------------------------
So after all of that, we find that our solutions are
 (from sin(x)=0) or (from sin(x)=0) or  or or  or or 
As always, we can check our work by using a calculator.
This is a lot to take in, so feel free to ask me further about any of this.
|
|
|