SOLUTION: How do I Solve the trigonometric equation for 1)tan3x=1

Algebra ->  Trigonometry-basics -> SOLUTION: How do I Solve the trigonometric equation for 1)tan3x=1       Log On


   

Question 756874: How do I Solve the trigonometric equation for
1)tan3x=1

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
One solution for tan%283x%29=1 comes from 3x=45%5Eo or 3x=pi%2F4.
The period of the function tangent is 180%5Eo or pi, so we can express all solutions, using k= any integer, as
3x=45%5Eo%2Bk%2A180%5Eo --> x=%2845%5Eo%2Bk%2A180%5Eo%29%2F3 --> highlight%28x=15%5Eo%2Bk%2A60%5Eo%29 or
3x=pi%2F4%2Bk%2Api --> x=%28%28pi%2F4%2Bk%2Api%29%29%2F3 --> x=pi%2F12%2Bk%2Api%2F3 --> x=pi%2F12%2B4k%2Api%2F12 --> highlight%28x=%284k%2B1%29pi%2F12%29

EXTRA:
If you are looking for solutions between 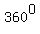0%5Eo and 360%5EO,
k=0 --> highlight%28x=15%5Eo%29,
k=1 --> x=15%5Eo%2B1%2A60%5Eo --> x=15%5Eo%2B60%5Eo --> highlight%28x=75%5Eo%29,
k=2 --> x=15%5Eo%2B2%2A60%5Eo --> x=15%5Eo%2B120%5Eo --> highlight%28x=135%5Eo%29,
k=3 --> x=15%5Eo%2B3%2A60%5Eo --> x=15%5Eo%2B180%5Eo --> highlight%28x=195%5Eo%29,
k=4 --> x=15%5Eo%2B4%2A60%5Eo --> x=15%5Eo%2B240%5Eo --> highlight%28x=255%5Eo%29,
k=5 --> x=15%5Eo%2B5%2A60%5Eo --> x=15%5Eo%2B300%5Eo --> highlight%28x=315%5Eo%29
We stop at k=5 because
k=6 --> x=15%5Eo%2B6%2A60%5Eo --> x=15%5Eo%2B360%5Eo=375%3E360%5Eo

Measuring angles in radians instead of degrees, the solutions for 0%3C=x%3C2pi
can be calculated from x=%284k%2B1%29pi%2F12 making k= 0, 1, 2, 3, 4, and 5.
k=0 --> highlight%28x=pi%2F12%29,
k=1 --> x=%284%2A1%2B1%29pi%2F12 --> highlight%285pi%2F12%29
k=2 --> x=%284%2A2%2B1%29pi%2F12 --> highlight%289pi%2F12%29
k=3 --> x=%284%2A3%2B1%29pi%2F12 --> highlight%2813pi%2F12%29
k=4 --> x=%284%2A4%2B1%29pi%2F12 --> highlight%2817pi%2F12%29
k=5 --> x=%284%2A5%2B1%29pi%2F12 --> highlight%2821pi%2F12%29