SOLUTION: To whom it may concern, what is the relationship between cotangent theta and cotangent NEGATIVE theta? Can you please give me 7 or 10 examples to work with. I really need to learn

Algebra ->  Trigonometry-basics -> SOLUTION: To whom it may concern, what is the relationship between cotangent theta and cotangent NEGATIVE theta? Can you please give me 7 or 10 examples to work with. I really need to learn      Log On


   

Question 689854: To whom it may concern,
what is the relationship between cotangent theta and cotangent NEGATIVE theta? Can you please give me 7 or 10 examples to work with. I really need to learn this immediately for an upcoming exam. Please reply ASAP. A thousand thank yous won't be enough.
-Lex
Found 2 solutions by KMST, lwsshak3:
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
cot%28theta%29=-cot%28-theta%29 because
cot%28theta%29=cos%28theta%29%2Fsin%28theta%29,
cot%28-theta%29=cos%28-theta%29%2Fsin%28-theta%29 and,
as sin%28theta%29=-sin%28-theta%29 and cos%28theta%29=cos%28-theta%29, then

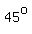Angles measuring 30%5Eo (AOB), 45%5Eo (AOC), 60%5Eo (AOD), ... are represented.

For the 30%5Eo or pi%2F6 angle AOB:
sin%28AOB%29=1%2F2=PB, and cos%28AOB%29=sqrt%283%29%2F2=OP are the x and y coordinates of point B
cot%28AOB%29=sqrt%283%29
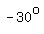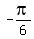The reflection of angle AOB is the -30%5Eo or -pi%2F6 angle AOB':
sin%28-30%5Eo%29=-1%2F2, cos%28-30%5Eo%29=sqrt%283%29%2F2, and cot%28-30%5Eo%29=-sqrt%283%29

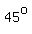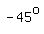For the 45%5Eo angle AOC and its reflection, the -45%5Eo angle AOC':
sin%2845%5Eo%29=sqrt%282%29%2F2, cos%2845%5Eo%29=sqrt%282%29%2F2,
sin%28-45%5Eo%29=-sqrt%282%29%2F2, and cos%28-45%5Eo%29=sqrt%282%29%2F2, so
cot%2845%5Eo%29=1 cot%28-45%5Eo%29=-1

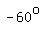For the 60%5Eo angle AOD and its reflection, the -60%5Eo angle AOD':
sin%2860%5Eo%29=sqrt%283%29%2F2, cos%2860%5Eo%29=1%2F2,
sin%28-60%5Eo%29=sqrt%283%29%2F2, and cos%28-60%5Eo%29=1%2F2, so
cot%2860%5Eo%29=1%2Fsqrt%283%29=sqrt%283%29%2F3 and cot%28-60%5Eo%29=-1%2Fsqrt%283%29=-sqrt%283%29%2F3

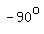For the 90%5Eo angle AOE and its reflection, the -90%5Eo angle AOE':
sin%2890%5Eo%29=1, cos%2890%5Eo%29=0,
sin%28-90%5Eo%29=1, and cos%28-90%5Eo%29=0, so
cot%2890%5Eo%29=0 cot%28-90%5Eo%29=0

Answer by lwsshak3(11628) About Me  (Show Source):
You can put this solution on YOUR website!
what is the relationship between cotangent theta and cotangent NEGATIVE theta?
cot(x)=-cot(-x) (this is called an odd function, compared to an even function)
Examples:
pick angle of 45º in quadrant I
this gives you a reference angle of 45º where cot 45º=1
-45º will also give you a reference angle of 45º but in quadrant IV where cot -45=-1
..
pick angle 135º in quadrant II
this gives you a reference angle of 45º where cot135º=-1
-135º will also give you a reference angle of 45º but in quadrant III where cot-135º=1
..
pick angle 225º in quadrant III
this gives you a reference angle of 45º where cot225º=1
-225º will also give you a reference angle of 45º but in quadrant II where cot-225º=-1
..
note: I used a reference angle of 45º for the examples but this will hold true for any reference angle.
This will also hold true for the tan function since cot is the reciprocal of tan.
A negative angle means rotating in a clockwise direction and a positive angle in a counter-clockwise direction.The value for the trig functions and their reciprocals is computed from the reference angle and the sign depends on which of the 4 quadrants the angle is in. See if you can apply this method to the sin and cos functions.
..
Hope this helps!