Question 596438: find all solutions of the equation in the interval [0,2pi] algebraically
cos2x+cosx=0
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solving these problems can be broken down into three stages:- Using Trig properties and/or algebra, transform the given equation into one or more equations of the form:
TrigFunction(variable-expression) = some-number - Find the general solution for the equation(s) from part 1
- If the problem asks for solutions in a specific interval, like yours, use the general solution (step 2) to find the specific solution(s) in the given interval.
cos(2x) + cos(x) = 0
Try as we might, there is no way to achieve the desired form using just algebra. So we'll need to use one or more Trig properties to replace one or more parts of the equation. We have properties for cos(2x) so we can replace that part of the expression. With cos(2x) we actually have three versions:I'm going to use the second one because the equation will only have cos (no sin) and having just the one function usually makes the desired form easier to achieve:

Notice the use of parentheses. It is an extremely good habit to use parentheses when substituting one expression for another. In this case it doesn't make much difference but many times it will help you avoid making a mistake. Simplifying we get:

The squared term makes this a quadratic equation. To solve for cos(x) we will need one side to be zero (which we already have) and then factor (or use the Quadratic Formula). Factoring is easier if the terms are in order. Rearranging the terms we get:

Factoring we get:
(2cos(x) - 1)(cos(x) + 1) = 0
(If you have trouble seeing how this factoring was done, it may help to think of cos(x) as some variable. Let's say cos(x) = q. Then  becomes becomes  . You should be able to see that this factors into (2q-1)(q+1) = 0. Then just put cos(x) back in for q.) . You should be able to see that this factors into (2q-1)(q+1) = 0. Then just put cos(x) back in for q.)
Now we can use the Zero Product Property which tells us that this (or any product) can be zero only if one (or more) of the factors is zero. So:
2cos(x) - 1 = 0 or cos(x) + 1) = 0
Solving each of these for cos(x) we get:
cos(x) = 1/2 or cos(x) = -1
After all this we have finally transformed the original equation into the desired form. (Fortunately this is usually the longest, hardest part of these problems.)
Now we find the general solution. Cosines of 1/2 and -1 should be recognizable. Only special angles have a cos of 1/2 or -1. For a cos of 1/2, the reference angle must be  and the angle must terminate in the 1st or 4th quadrant. This gives us: and the angle must terminate in the 1st or 4th quadrant. This gives us:

or

And for cos(x) = -1 there is only one angle,  , so: , so:

(Remember, all angles co-terminal with  , , 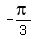 or or  will also work. That is what the "+ will also work. That is what the "+ 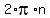 " is about. This is how we can express all the co-terminal angles mathematically. The "n" can be any integer and by using different values for n you get different but co-terminal angles.) " is about. This is how we can express all the co-terminal angles mathematically. The "n" can be any integer and by using different values for n you get different but co-terminal angles.)
So the general solution is:

or

or

Last of all we find the specific solution(s) that are in the interval [0,  ). For this we take each equation and try different integer values for n until you have found all the solutions in the desired interval. It just so happens that you get only one solution in the interval from each of the three equations. (Note: Sometimes you might get more than one solution in the interval from an equation so don't just stop as soon as you find one. Also, there might be times when an equation from the general solution will not give you any solutions in the interval.) ). For this we take each equation and try different integer values for n until you have found all the solutions in the desired interval. It just so happens that you get only one solution in the interval from each of the three equations. (Note: Sometimes you might get more than one solution in the interval from an equation so don't just stop as soon as you find one. Also, there might be times when an equation from the general solution will not give you any solutions in the interval.)
When n = 0 in the first equation you get 
When n = 1 in the second equation you get 
When n = 0 in the third equation you get 
|
|
|