y= π-3sin^-1 (1-4x) from y=sin^-1 x
To find out the operations, we must first "route out" the path
from y = sin-1(x) to y = p - 3sin-1(1 - 4x)
To find the "route", we change the expression in
y = f(x) to y = A*f[B(x+C)] + D
First we change the expression in parentheses to the form B(x+C)
in parentheses:
1 - 4x
Write it in descending order
-4x + 1
Factor out the coefficient of x
-4(x -  )
So to build that expression from x
one operation at a time of replacing x:
We go from x to -x to -4x to -4(x -
)
So to build that expression from x
one operation at a time of replacing x:
We go from x to -x to -4x to -4(x -  )
which means we go from the graph of
y = sin-1(x)
to the graph of
y = sin-1(-x)
to the graph of
y = sin-1(-4x)}}})
to the graph of
y = sin-1[-4(x -
)
which means we go from the graph of
y = sin-1(x)
to the graph of
y = sin-1(-x)
to the graph of
y = sin-1(-4x)}}})
to the graph of
y = sin-1[-4(x -  )]
to the graph of
y = -sin-1[-4(x -
)]
to the graph of
y = -sin-1[-4(x -  )]
to the graph of
y = -3sin-1[-4(x -
)]
to the graph of
y = -3sin-1[-4(x -  )]
to the graph of
y = -3sin-1[-4(x -
)]
to the graph of
y = -3sin-1[-4(x -  )] + p
The first operation in going from the graph of
y = sin-1(x)
which is this
)] + p
The first operation in going from the graph of
y = sin-1(x)
which is this
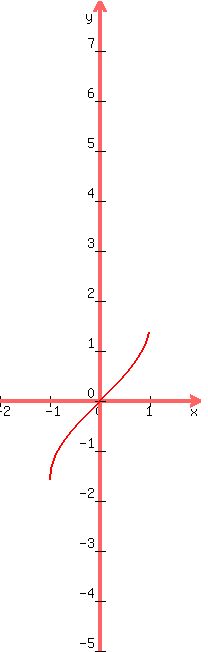 to the graph of
y = sin-1(-x)
involves replacing x by -x which is a
reflection across (or into) the y-axis:
to the graph of
y = sin-1(-x)
involves replacing x by -x which is a
reflection across (or into) the y-axis:
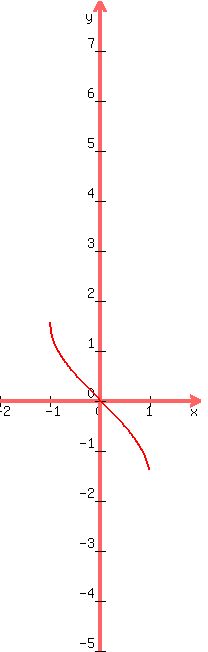 Next we go from that graph to the graph of
y = sin-1(-4x)
That involves replacing x by 4x which is a
horizontal shrinking of the graph by a factor of
Next we go from that graph to the graph of
y = sin-1(-4x)
That involves replacing x by 4x which is a
horizontal shrinking of the graph by a factor of  :
:
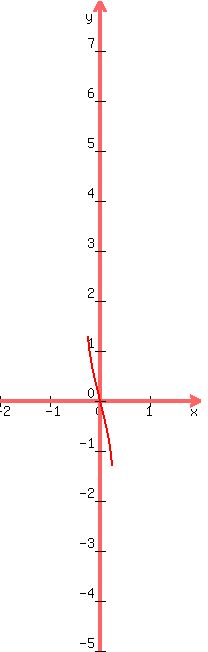 Next we go from that graph to the graph of
y = sin-1[-4(x -
Next we go from that graph to the graph of
y = sin-1[-4(x -  )]
That involves replacing x by x -
)]
That involves replacing x by x -  which is a right shift of
which is a right shift of  a unit:
a unit:
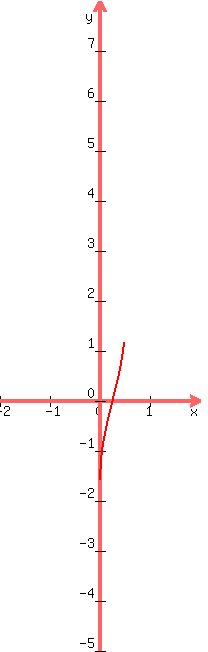
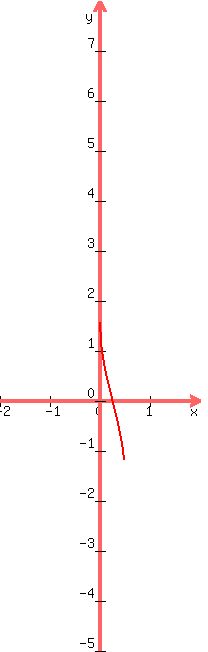 Now we go from that graph to the graph of
y = -sin-1[-4(x -
Now we go from that graph to the graph of
y = -sin-1[-4(x -  )]
which involves multiplying the whole right side by -1,
which reflects the graph across (or into) the
x-axis:
)]
which involves multiplying the whole right side by -1,
which reflects the graph across (or into) the
x-axis:
 Now we go from that graph to the graph of
y = -3sin-1[-4(x -
Now we go from that graph to the graph of
y = -3sin-1[-4(x -  )]
which involves multiplying the whole right side by 3,
which stretches the graph by a factor of 3
)]
which involves multiplying the whole right side by 3,
which stretches the graph by a factor of 3
 Finally we go from that graph to the graph of
y = -3sin-1[-4(x -
Finally we go from that graph to the graph of
y = -3sin-1[-4(x -  )] + p
which involves adding p to the right side,
which shifts the graph vertically p units upward:
)] + p
which involves adding p to the right side,
which shifts the graph vertically p units upward:
 Edwin
Edwin