The basic problem is to convert revolutions to radians and minutes to seconds. One complete revolution is  radians. And 1 minute equals 60 seconds.
radians. And 1 minute equals 60 seconds.
When converting units like this, if you are unsure of whether to multiply or divide, you can use what I call unit Algebra to help. Just make a fraction of your conversions and include the units. There will two ways to make these fractions depending on which unit you decide to put on top. Here are the possibel fractions for this problem:
1 revolution
________________
 radians
radians
 radians
__________________
1 revolution
1 minute
____________
60 seconds
60 seconds
____________
1 minute
radians
__________________
1 revolution
1 minute
____________
60 seconds
60 seconds
____________
1 minute
The tough part of this is understanding that all these fractions are 1's!! Although the numbers in the numerators and denominators are not the same as we would usually expect in a fraction that equals one, the numerators and denominators are equal. After all, isn't 1 minute the same amount of time as 60 seconds?
Now we just figure out which of the fractions to use. What we will be doing is multiplying
1500 revolutions
________________
1 minute
by two of these fractions and, since multiplying by 1's (no matter how weird they look) does not change the number, we will be able to get the answer we want.
Let's try
1500 revolutions 1 revolution 60 seconds
________________ * _________________ * __________
1 minute  radians 1 minute
radians 1 minute
We want an answer that is radians/second. So we want the minutes and revolutions to disappear. We want them to cancel. But with the expression above, "revolution" is in 2 numerators and no denominators. So they will not cancel. Similarly the "minutes" are in 2 denominators but no numerators. So they do not cancel either. We want "revolutions" and "minutes" to appear in the numerator and denominator the same number of times so they all cancel out.
Let's see how the correct choice of fractions looks:
1500 revolutions  radians 1 minute
________________ * _________________ * ___________
1 minute 1 revolution 60 seconds
radians 1 minute
________________ * _________________ * ___________
1 minute 1 revolution 60 seconds
"revolutions" and "minutes" each appear once in the numerator and once in the denominator. So they will cancel out. The units that will remain are "radians" in the numerator and "seconds" in the denominator which is exactly what we are looking for. After canceling the "revolutions" and "minutes" we are left with:
1500  radians 1
____ * _________________ * ____________
1 1 60 seconds
radians 1
____ * _________________ * ____________
1 1 60 seconds
Since 1500/60 = 25 this simplifies to:
25* radians
____________________
1 second
radians
____________________
1 second
which simplifies to
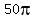 radians
____________________
1 second
radians
____________________
1 second
Although this does not match any of the answers you provided, it is the correct answer for the problem you described.