Question 173155: sorry, these problems aren't from a textbook. I've started these four problems then just started going in circles to find the answer.
1.)Solve for x, where x is between 0 and 2pie
tan^(2)x-tanx-3=0
2.)verify the identity:
sinx/1-cos=cscx+cotx
where 0
3.)evaluate:
cos[sin^(-1)(3/5)]
4.) Given that sin theta =1/2, theta in Q1 and cos beta =1/2, find cos (theta-bata)
much appreciated!!
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1.)Solve for x, where x is between  and and 

Write  for for 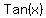
 That doesn't factor, so we use the quadratic formula:
That doesn't factor, so we use the quadratic formula:
 with
with  , ,  , and , and  : :


 Using the +
Using the +
 Replace
Replace  by by 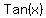
 Use inverse tangent key on calculator,
with calculator in radian mode:
Use inverse tangent key on calculator,
with calculator in radian mode:
 However, the calculator only gives the
answer which is in quadrant I. There is
also another answer in quadrant III, because
the tangent is also positive in quadrant III.
To get that, we add
However, the calculator only gives the
answer which is in quadrant I. There is
also another answer in quadrant III, because
the tangent is also positive in quadrant III.
To get that, we add  : :
 Using the minus:
Using the minus:

 Use inverse tangent key on calculator,
with calculator in radian mode:
Use inverse tangent key on calculator,
with calculator in radian mode:
 However, the calculator only gives the
negative answer which is in quadrant IV,
taken as a negative angle. However to get
a coterminal angle between 0 and
However, the calculator only gives the
negative answer which is in quadrant IV,
taken as a negative angle. However to get
a coterminal angle between 0 and  ,
we add ,
we add  : :
 There is also another answer in quadrant II,
because the tangent is also negative in quadrant IV.
To get that, we add
There is also another answer in quadrant II,
because the tangent is also negative in quadrant IV.
To get that, we add  to the to the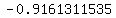
 2.)verify the identity:
2.)verify the identity:
 3.)evaluate:
3.)evaluate:
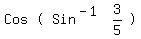 Let's draw the picture of
Let's draw the picture of 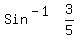 That means the angle whose sine is
That means the angle whose sine is  The inverse sine by definition is always between
The inverse sine by definition is always between
 and and  . Thus the angle . Thus the angle 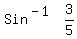 is in Quadrant I because is in Quadrant I because  is a positive number.
Since the sine =
is a positive number.
Since the sine =  we will let y be
the numerator of we will let y be
the numerator of  and r be the
denominator.
The angle and r be the
denominator.
The angle 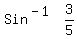 is is
 Now we need the cosine of this angle, which is
Now we need the cosine of this angle, which is  , so
we will need the value of , so
we will need the value of  . We use the Pythagorean theorem, . We use the Pythagorean theorem,






 So now we have
So now we have  , so we put that in: , so we put that in:
 Therefore the cosine of that angle is
Therefore the cosine of that angle is  or or  So,
So,
 If I have time I'll come back to this:
4.) Given that sin theta =1/2, theta in Q1 and cos beta =1/2, find cos (theta-bata)
Edwin
If I have time I'll come back to this:
4.) Given that sin theta =1/2, theta in Q1 and cos beta =1/2, find cos (theta-bata)
Edwin
|
|
|