SOLUTION: what is the derivative of -CSCxCotx? I know how to start it but i dont know how to symplify the last step CSCx((CSCx)^2+(Cotx)^2)?

You have demonstrated the fact that there are sometimes many
ways to "play around" with the trigonometric identities, and one 
trigonometric expression may not necessarily be better or worse, 
nor simpler or more complicated, than another. Oftentimes it is
just a matter of personal preference. 

I'll start from scratch even though your derivative is perfectly 
correct: 



Leave the negative sign factored out:







Now remove the parentheses:

 

Now factor out a CSCx



That's where you got to.  That may very
well be simple enough as it is. 

Some people might argue we should write
the  in terms of 
so that it would involve only one trig
function, the cosecant, like this: 





Then someone else may argue that the 
secants, cosecant, and cotangents are not
as desirable as sines and cosines.

They would perhaps change everything 
to sines and cosines:







Some may consider that simpler.  Others would say
the form you got to was simpler because there were
no fractions.

Still others might say the one in sines and
cosines would be simpler if it were all in just
sines with no cosines, so they would replace
the 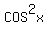 by .







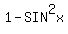There is no hard fast rule in all cases as to what 
trigonometric form is considered the best or 
the simplest.

Edwin