.
Determine the constants a and b so that  for all values of x.
for all values of x.
~~~~~~~~~~~~~~~~~
Transform the numerator step by step
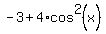 =
= 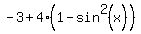 =
= 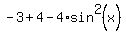 =
= 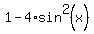 =
= 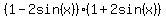 .
So, your fraction now is
.
So, your fraction now is
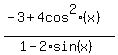 =
= 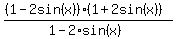 .
Cancel the factors ((1-2*sin(x)) in both the numerator and denominator. You will get then
.
Cancel the factors ((1-2*sin(x)) in both the numerator and denominator. You will get then
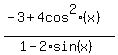 =
= 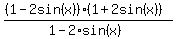 = 1 + 2*sin(x).
It is just the form which you need. So, a= 1, b= 2.
ANSWER. a= 1, b= 2.
= 1 + 2*sin(x).
It is just the form which you need. So, a= 1, b= 2.
ANSWER. a= 1, b= 2.
Solved.