SOLUTION: An observer 9m. horizontally away from the tower observes its angle of elevation to be only one half as much as the angle of elevation of the same tower when he moves 5m. nearer to

Algebra ->  Trigonometry-basics -> SOLUTION: An observer 9m. horizontally away from the tower observes its angle of elevation to be only one half as much as the angle of elevation of the same tower when he moves 5m. nearer to      Log On


   

Question 1187818: An observer 9m. horizontally away from the tower observes its angle of elevation to be only one half as much as the angle of elevation of the same tower when he moves 5m. nearer towards the tower. How high is the tower?
Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.
An observer 9 meters horizontally away from the tower observes its angle of elevation to be only one half
as much as the angle of elevation of the same tower when he moves 5 meters nearer towards the tower.
How high is the tower?
~~~~~~~~~~~~


            It is a good  Trigonometry problem,  and it deserves a detailed explanation.

            See my solution below.  Read it attentively. 


Let h be the height of the tower.


First position is 9 meters from the tower.  In this position,

    tan(a) = h%2F9,  where "a" is the angle of elevation in this position.    (1)


Next position is  (9-5) = 4 meters from the tower.  In this position,

    tan(b) = h%2F4,  where "b" is the angle of elevation in this position.    (2)


We are given  b = 2a.  Hence,

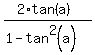    tan(b) = tan(2a) = (use the basic Trigonometry formula) = %282%2Atan%28a%29%29%2F%281-tan%5E2%28a%29%29 = 


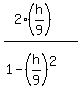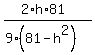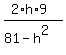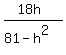           = %282%2A%28h%2F9%29%29%2F%281+-+%28h%2F9%29%5E2%29 = (simplify) = %282%2Ah%2A81%29%2F%289%2A%2881-h%5E2%29%29 = %282%2Ah%2A9%29%2F%2881-h%5E2%29 = %2818h%29%2F%2881-h%5E2%29.


Thus from (2) we have THIS EQUATION

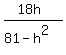    %2818h%29%2F%2881-h%5E2%29 = h%2F4.


Cancel common factor "h" in both sides; then cross-multiply to get

    18*4 = 81 - h^2

     72  = 81 - h^2

    h^2 = 81 - 72 = 9.


Hence,  h = sqrt%289%29 = 3.


ANSWER.  The tower height is 3 meters.

Solved and thoroughly explained.