Question 1187817: A flagpole 20m. high stands on top of a tower which is 96m. high. At what distance from the base of the tower will the flagpole subtend an angle of 4degrees.
Found 2 solutions by ankor@dixie-net.com, ikleyn:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A flagpole 20m. high stands on top of a tower which is 96m. high.
At what distance from the base of the tower will the flagpole subtend an angle of 4degrees.
:
Draw this out as a right triangle, with the angle of 4 degrees from the base to the top of the flagpole
:
Height of the flagpole 20 + 96 = 116 m
let d = the distance the 4 degree angle is from the base of the tower
Flagpole is the side opposite the 4 degree angle. Distance from the base is the side adjacent
tan(4) = 
tan(4)*d = 116
.069927d = 116
d = 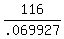
d = 1659 meters
Answer by ikleyn(52800)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A flagpole 20m. high stands on top of a tower which is 96m. high. At what distance from the base
of the tower will the flagpole subtend an angle of 4 degrees.
~~~~~~~~~~~~~~~~~~~~
The solution given by tutor @ankor@dixie-net.com is, unfortunately, INCORRECT.
It is CONCEPTUALLY INCORRECT.
I came to bring you the correct solution.
So, we are given the height of the tower of 96 m and the height of the flagpole of 20 m.
The entire construction is 96+20 = 116 m height.
Let's d be the sough horizontal distance from the tower.
Let " a " be the visibility angle for the tower and let " b " be the visibility angle
for the entire construction.
Obviously, tan(a) = 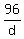 ; tan(b) = ; tan(b) =  .
They want we find the distance d in a way that the difference of angles "a" and "b" be 4°:
b - a = 4°, or, equivalently, tan(b-a) = tan(4°) = 0.07. (1)
Use the formula tan(b-a) = .
They want we find the distance d in a way that the difference of angles "a" and "b" be 4°:
b - a = 4°, or, equivalently, tan(b-a) = tan(4°) = 0.07. (1)
Use the formula tan(b-a) = 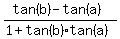 . So,
tan(a-b) = . So,
tan(a-b) = 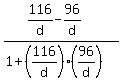 = = 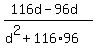 = =  .
So, equation (1) takes the form .
So, equation (1) takes the form
 = 0.07,
or
d^2 + 11136 = = 0.07,
or
d^2 + 11136 = 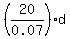 ,
d^2 - 285.7143d + 11136 = 0.
Use the quadratic formula (I used one of the numerous online solvers).
The roots are d= 239.149 and d= 46.565.
ANSWER. There are two possible solutions: the distances are 239.149 meters and/or 46.565 meters.
CHECK. I checked the solution, using arctan function, and the check CONFIRMED that the answer is correct. ,
d^2 - 285.7143d + 11136 = 0.
Use the quadratic formula (I used one of the numerous online solvers).
The roots are d= 239.149 and d= 46.565.
ANSWER. There are two possible solutions: the distances are 239.149 meters and/or 46.565 meters.
CHECK. I checked the solution, using arctan function, and the check CONFIRMED that the answer is correct.
Solved.
|
|
|