SOLUTION: The length of the sides of a triangle are 12,15 and 18. A circle tangent to the longest and shortest side has its center on the remaining side. Find the distance from the center of

Algebra ->  Trigonometry-basics -> SOLUTION: The length of the sides of a triangle are 12,15 and 18. A circle tangent to the longest and shortest side has its center on the remaining side. Find the distance from the center of      Log On


   

Question 1159374: The length of the sides of a triangle are 12,15 and 18. A circle tangent to the longest and shortest side has its center on the remaining side. Find the distance from the center of the circle to the midpoint of the side where the center of the circle lies.
Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.

The center of this circle lies on the angle bisector drawn to the 15 units side.


So, the center of the circle is the intersection point of this angle bisector with the 15 units side.


According to the well known property of the angle bisectors in triangles, the base point of the angle bisector 
divides the corresponding side of the triangle in parts proportional to lateral side lengths.


So, in our case, the angle bisector divides the 15 unit side in proportion 12:18.


Thus the parts of the 15 units side are 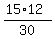15%2A%2812%2F%2812%2B18%29%29 = %2815%2A12%29%2F30 = 6 units  and  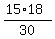15%2A%2818%2F%2812%2B18%29%29 = %2815%2A18%29%2F30 = 9 units.


Thus, the center of the circle is  15%2F2+-+6 = 7.5-6 = 1.5 units from the midpoint of the 15-units side.    ANSWER