Question 1155366: Please help me to answer this:
For 0° ≤ x ≤ 360°, find the number of roots the equation 2sinxtanx = -tanx
Found 2 solutions by math_helper, Theo:
Answer by math_helper(2461)   (Show Source):
You can put this solution on YOUR website! The first thing is to look for zeros:
tan(x)=0 at 0, 180, and 360 degrees, and these are all solutions.
For non-zero solutions:
Simplify  to  ,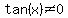 
and recall:
 and
in Q1,Q2,Q3,Q4, sin(x) is +,+,-,-, respectively.
Working from the x-axis, push the angle into Q3 by adding 180+30 = 210 and into Q4 by subtracting 30 from 360, giving 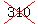 330 (edited typo here).
Solutions are 
A picture is worth a thousand words:
And note if you rearrange to 2sin(x)tan(x)+tan(x) = 0 and graph the LHS, you can simply look for where this rearranged function crosses the x-axis:
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! i believe this will have 5 roots between 0 and 360 degrees.
the roots will be at 0, 180, 360 degrees for tan(x) = 0, and 210, 330 degrees for sin(x) = -1/2.
to confirm, graph the equation as shown below:
to solve algebraically, do the following.
start with 2 * sin(x) * tan(x) = -tan(x)
add tan(x) to both sides of the equation to get:
2 * sin(x) * tan(x) + tan(x) = 0
factor out tan(x) to get:
tan(x) * (2 * sin(x) + 1) = 0
this is true when tan(x) = 0 or sin(x) + 1 = 0
when tan(x) = 0, x = 0 or 180 or 360 degrees.
when 2 * sin(x) + 1 = 0, solve for sin(x) to get:
sin(x) = -1/2
solve for sin(x) = plus 1/2 to get x = 30 degrees.
that's in the first quadrant where all trig functions are positive and where all reference angles reside.
sine is negative in the third and fourth quadrants.
in the third quadrant 180 + 30 = 210 degrees.
in the fourth quadrant 360 - 30 = 330 degrees.
confirm by solving for sin in all 4 quadrants to see that the sine is only negative in the third and fourth quadrant.
30 degrees in the second quadrant = 180 - 30 = 150.
30 degrees in the third quadrant = 180 + 30 = 210.
30 degrees in the fourth quadrant = 360 - 30 = 330 degrees.
sin(30) = 1/2
sin(150) = 1/2
sin(210) = -1/2
sin(330) = -1/2
the sine is -1/2 at 210 and 330 degrees only in the interval between 0 and 360 degrees.
bottom line:
5 roots.
0, 180, 360 for tan(x0 = 0
210 and 330 for sin(x0 = -1/2
|
|
|
