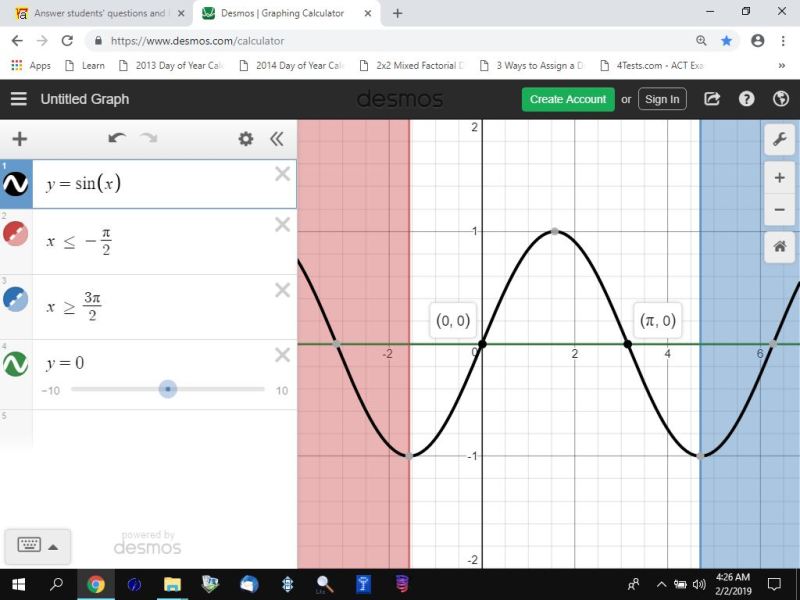
Question 1133868: Refer to the graph of y = sin x to find the exact values of x in the interval
(−π/2, 3π/2) that satisfy the equation. (Enter your answers as a comma-separated list.)
sin x = 0
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! sin(x) = 0 when x = 0 or 180 or 360 or -180 or -360, etc.
the general formula would be sin(x) = 0 when x = 0 plus or minus k * 180, where k = any positive integer.
when you're dealing with radians, the general formula would be sin(x) = 0 when x = 0 plus or minus k * pi.
that's because pi radians is equal to 180 degees.
the conversion factor is degrees = radians * 180 / pi and radians = degrees * pi / 180.
so 180 degrees * pi / 180 = pi radians and pi radians * 180 / pi = 180 degrees.
your interval of interest is -pi/2 radians to 3pi/2 radians.
-pi/2 radians * 180 / pi = -90 degrees.
3pi/2 radians * 180 / pi = 270 degrees.
your interval in radians is -pi/2 to 3pi/2 radians.
you interval in degrees is - 90 to 270 degrees.
in degrees, the general formula of sin(x) = 0 when x = 0 plus or minus 180 degrees will get you x = 0, 180, 360, 540, ... and x = 0, -180, -360, -540, ... .
0 and 180 are in the interval between -90 and 270 degrees, so they have to be your answer.
in radians, the general formula of sin(x) = 0 when x = 0 plus or minus pi radians will, get you x = 0, pi, 2pi, 3pi, .... and x = 0, -pi, -2pi, -3pi, ... .
in the interval between -pi/2 and 3pi/2, x = 0 and pi fits.
in degrees, x is equal to 0 or 180 degrees.
in radians, x is equal to 0 or pi radians.
the first graph shows you this in degrees.

the second graph shows you this in radians.
|
|
|