Question 1127027: To a motor-cyclist traveling due north at 50km/hr, the wind appear to come from north west at 60km/hr, what is the true velocity of the wind
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1. Let's consider more simple case first:
Let there is no wind at the coordinate system which rests relative the Earth,
and a motor-cyclist travels due North at 50 km/h.
Then it is clear that he/she will observe the wind due to south at 50 km/h.
I other words, he/she will observe the wind with the vector (0,-50) (the units of speed are in km/h).
2. Then it is clear, that if there is the wind with the velocity vector W
in the coordinate system which rests relative the Earth surface, and
the motor-cyclist moves at the speed M (! M is vector !), then the wind he/she will observe is 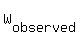 = W - M.
3. With these explanations, we have
- the vector M = (0,50) of the motor-cyclist speed relative the Earth;
- the vector = W - M.
3. With these explanations, we have
- the vector M = (0,50) of the motor-cyclist speed relative the Earth;
- the vector 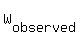 = ( = (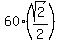 , ,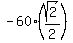 )
- and the equation )
- and the equation 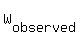 = ( = (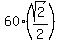 , ,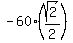 ) = W - (0,50).
From this equation, the "real" vector of the wind velocity in the resting coordinate system is
W = ( ) = W - (0,50).
From this equation, the "real" vector of the wind velocity in the resting coordinate system is
W = (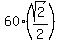 , ,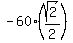 ) + (0,50) = ( ) + (0,50) = (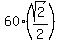 , ,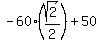 ).
Now, when you know the vector W by its components, you can easily calculate its magnitude.
It is just arithmetic, and I leave it to you to complete this assignment on your own. ).
Now, when you know the vector W by its components, you can easily calculate its magnitude.
It is just arithmetic, and I leave it to you to complete this assignment on your own.
So, by explaining all these details to you, I consider my function as a tutor fully completed.
|
|
|