Question 1125018: Using the graph of y=sin(x), list all values on the interval [-8pi/3, 13pi/6] that satisfy the ordered pair (x,1/2).
List all the values that satisfy (x,1/2).
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the angles are:
-11pi/6, -7pi/6, pi/6, 5pi/6, 13pi/6
first thing you do is find the angle in the first quadrant.
sin^-1(1/2) = pi/6 radians.
multiply that by 180 / pi and it becomes 30 degrees.
this makes sense since sin(30 degrees) = 1/2.
sine is positive in the first and second quadrant.
the equivalent angle in the second quadrant is pi - pi/6 = 5pi/6 radians.
that's equivalent to 180 - 30 = 150 degrees.
5pi/6 * 180 / pi = 5/6 * 180 = 150 degrees.
that also makes sense.
these angles will repeat every 360 degrees or every 2 pi radians.
2pi radians is equivalent to 12pi / 6 radians.
pi / 6 + 12pi / 6 = 13pi / 6.
that's as far as you want to go in the positive direction.
so far your angles are pi/6, 5pi/6, 13pi/6.
in the other direction, pi/6 - 12pi / 6 = -11 pi/6.
you can't go down further than that because the limit is -16pi / 6 and subtracting another 12pi / 6 will go beyond that.
5pi / 6 - 12pi / 6 = -7pi / 6.
you can't go further than that because subtracting another 12pi / 6 will get you -17pi / 6 which is further than -16pi / 6.
your angles are therefore:
-11pi/6, -7pi/6, pio/6, 5pi/6, 13pi/6
all these angles will have 1/2 as their sine.
you can use your calculator to confirm.
alternatively, you can graph the equations to get what is shown below:
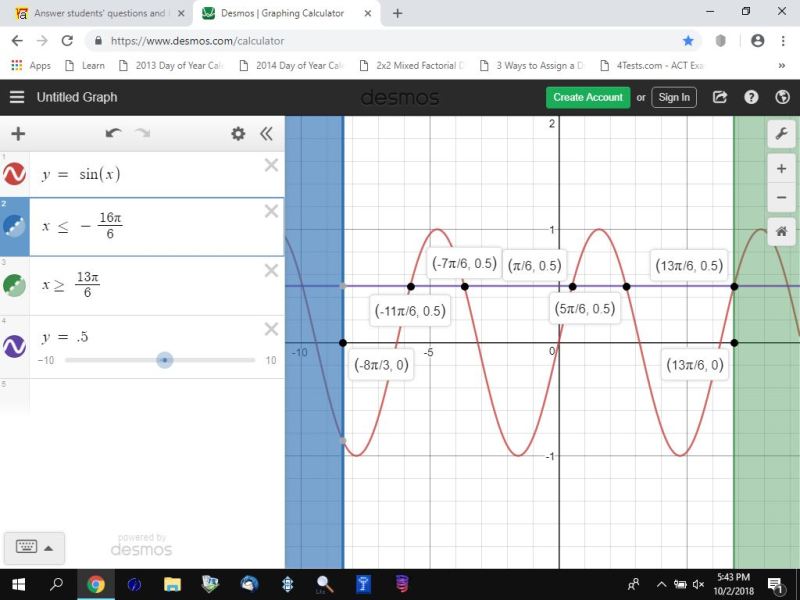
the graph of y = sin(x) is in red.
the graph of y = 1/2 is in purple.
the intersection of the red graph and and the purple graph shows the angles where sin(x) = 1/2.
the valid interval is between -16pi/6 and 13pi/6.
that's the unshaded area of the graph.
-16pi / 6 is the same angle as -8pi / 3.
rather than simplifying all the angles, i keep the denominators the same.
it's easier to see the intervals that way.
the graphing software will, however, do the simplification where it can.
|
|
|