.
1. tan(2A) = 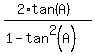 =
= 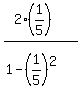 =
= 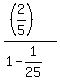 =
= 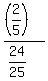 =
= 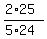 =
= 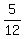 .
So, your calculations for tan(2A) are correct.
2. To calculate tan(4A), notice that 4A = 2*(2A); thus tan(4A) = tan(2*(2A)).
So, you can repeat THE SAME PROCEDURE to get tan(4A) starting from tan(2A), which you just know.
3. tan(45°-4A) =
.
So, your calculations for tan(2A) are correct.
2. To calculate tan(4A), notice that 4A = 2*(2A); thus tan(4A) = tan(2*(2A)).
So, you can repeat THE SAME PROCEDURE to get tan(4A) starting from tan(2A), which you just know.
3. tan(45°-4A) =  =
= 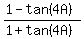 .
So, when you will find tan(4A) (as I described in n.2), you will be in position to find tan(45°-4A).
.
So, when you will find tan(4A) (as I described in n.2), you will be in position to find tan(45°-4A).