Question 1087682: Hello! I need help, please :(
A communications satellite is orbiting the Earth at a height of h miles above the plant’s surface. The satellite can transmit data to any point along an arc of length s miles on the Earth based on the “line of sight” from the satellite to the point on the arc. At the endpoints of the arc, the line of sight from the satellite to these points forms a right angle with a radius of the Earth, (assume the Earth is a sphere of radius 3960 mi). Let theta represent one-half of the central angle subtended by the arc as shown in the diagram at right.
(Here is the link to the diagram since I couldn't post the actual picture: http://imgur.com/a/ply9o)
a. Express the angle theta as a function of h.
b. Express the length of the arc, s, as a function of theta. (Don’t forget about radian measure)
c. Use composition of functions to find the length of the arc, s, as a function of h.
d. Since the angle and the arc length are both functions of the height of the satellite, it is this height that determines their values. Build a table for both functions showing their values for heights ranging from 0 miles to 1000 miles in increments of 100 miles.
e. Try using some values of h greater than 1000 to see what happens to theta and s, then discuss, intuitively, (using common sense), what the angle, theta, and the arc length, s, approach as h increases to infinity. Now, relate these ideas to the terms “domain” and “range”.
Answer by ikleyn(52786)   (Show Source):
You can put this solution on YOUR website! .
a. Express the angle theta as a function of h.
 =  .
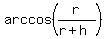b. Express the length of the arc, s, as a function of theta. (Don’t forget about radian measure)
s =  .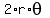
c. Use composition of functions to find the length of the arc, s, as a function of h.
s =  .
d. Since the angle and the arc length are both functions of the height of the satellite, it is this height that determines their values.
Build a table for both functions showing their values for heights ranging from 0 miles to 1000 miles in increments of 100 miles.
h, in miles theta (radians) s, in miles
100 0.222 1761
200 0.311 2466
300 0.378 2990
400 0.432 3419
500 0.478 3786
600 0.519 4109
700 0.555 4397
800 0.588 4659
900 0.618 4898
1000 0.646 5118
e. Try using some values of h greater than 1000 to see what happens to theta and s, then discuss, intuitively, (using common sense),
what the angle, theta, and the arc length, s, approach as h increases to infinity. Now, relate these ideas to the terms “domain” and “range”.
|
|
|
