q = sin-1(x)+cos-1(x)-tan-1(x) for the domain x ≥ 0,
what is the range?
Because of the inverse sine and cosine functions,
the domain of q is 0 ≤ x ≤ 1,
We find the derivative of q
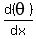
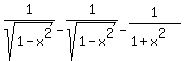The first two terms cancel and we have
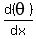
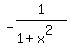Since the derivative of q is negative, the function q
decreases everywhere on the open part of its domain,
which is 0 < x < 1.
[q is not differentiable at the endpoints 0 and 1, although
q is defined at those endpoints]
We evaluate q at the endpoints of the
domain of q :
Substitute x = 0
q = sin-1(0) + cos-1(0) - tan-1(0) = 0° + 90° - 0° = 90°
Substitute x = 1
q = sin-1(1) + cos-1(1) - tan-1(1) = 90° + 0° - 45° = 45°
Thus the range for q for the domain
0 ≤ x ≤ 1
is
45° ≤ q ≤ 90°
Edwin
