Question 1052636: if an equilateral triangle is circumscribed about a circle of radius 10cm. determine the side of the triangle?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! The circle and equilateral triangle can be slices pizza-style into  wedges/triangles.
The right triangle shown above is one of those triangles.
It is a right triangle because the radius of the circle must be perpendicular to the tangent side of the equilateral triangle.
The angle at the center of the circle is  .
The side adjacent to that angle is the radius of the circle, and measures  .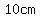
The opposite side, of length  , is  of the side of the equilateral triangle.
The trigonometric ratios tell us that
 ,
so   and   is the length of the side of the equilateral triangle.
Allergic to trigonometry? Then, you would have to use similar triangles and the Pythagorean theorem.
 Right triangles BCD and OAD are similar because their smallest angles are congruent. (Angles BCD and OAD are both half of an equilateral triangle's angle).
 is half of the equilateral triangle's side.
 is the equilateral triangle's side.
Since the triangles are similar, the ratio of long leg to short leg is
 or  ---> 
We can find CD, the long leg of BCD, using the Pythagorean theorem, because
 or  , and
--> --> --> .
So, plugging that into , we get
 --->
So the side of the equilateral triangle measures 
|
|
|
