SOLUTION: Please help me prove this identity by working on only ONE side of the equation (sin^3(A) + cos^3(A)) / (sin^2(A) + 2sin(A)cos(A) + cos^2(A)) = (1 / (sin(A) + cos(A))) - (cos(A) /

Algebra ->  Trigonometry-basics -> SOLUTION: Please help me prove this identity by working on only ONE side of the equation (sin^3(A) + cos^3(A)) / (sin^2(A) + 2sin(A)cos(A) + cos^2(A)) = (1 / (sin(A) + cos(A))) - (cos(A) /       Log On


   

Question 1023434: Please help me prove this identity by working on only ONE side of the equation
(sin^3(A) + cos^3(A)) / (sin^2(A) + 2sin(A)cos(A) + cos^2(A)) = (1 / (sin(A) + cos(A))) - (cos(A) / (1 + cot(A)))


Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
%22%22=%22%22
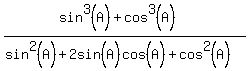
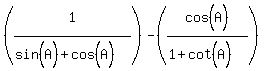
We work with the left side:



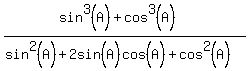Let s = sin(A) 
Let c = cos(A)

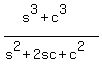%28s%5E3+%2B+c%5E3%29+%2F+%28s%5E2+%2B+2sc+%2B+c%5E2%29

Factor numerator as the sum of two cubes
and the trinomial in the denominator

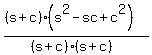%28%28s%2Bc%29%28s%5E2-sc%2Bc%5E2%29%29%2F%28%28s%2Bc%29%28s%2Bc%29%29

Cancel the (s+c)'s

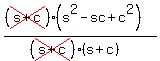
%28%28cross%28s%2Bc%29%29%28s%5E2-sc%2Bc%5E2%29%29%2F%28%28cross%28s%2Bc%29%29%28s%2Bc%29%29

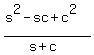%28s%5E2-sc%2Bc%5E2%29%2F%28s%2Bc%29

Replace s and c by what we let them be above:



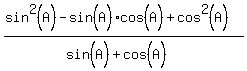By a well known identity, looking at the first
and third terms, the numerator becomes



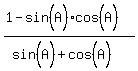We break that into two fractions:



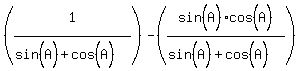In the second fraction, divide every term,
top and bottom by sin(A)



Cancel the sin(A)'s in the top, and the sin(A)'s in the bottom





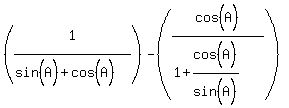By using a well-known identity for cot(A):



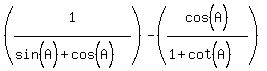Edwin