SOLUTION: There are two towers. One at A and one at B. A and B are are two points on the same horizontal ground and 120 m apart. The angle of elevation of the top of the tower at B as observ

Algebra ->  Trigonometry-basics -> SOLUTION: There are two towers. One at A and one at B. A and B are are two points on the same horizontal ground and 120 m apart. The angle of elevation of the top of the tower at B as observ      Log On


   

Question 1014220: There are two towers. One at A and one at B. A and B are are two points on the same horizontal ground and 120 m apart. The angle of elevation of the top of the tower at B as observed from A is twice that of the tower at A as observed at B. At C, midway between A and B, the angles of elevation are complimentary. Find the heights of the the towers.
I really need the answers ASAP. I'm going to pass this take home quiz tomorrow at 8:30 AM, Philippine time (GMT +8). I suck at math, so I don't know what to do. Thank you so so so much :)
Answer by ikleyn(52800) About Me  (Show Source):
You can put this solution on YOUR website!
.
There are two towers. One at A and one at B. A and B are are two points on the same horizontal ground and 120 m apart.
The angle of elevation of the top of the tower at B as observed from A is twice that of the tower at A as observed at B.
At C, midway between A and B, the angles of elevation are complimentary. Find the heights of the the towers.
I really need the answers ASAP. I'm going to pass this take home quiz tomorrow at 8:30 AM, Philippine time (GMT +8).
I suck at math, so I don't know what to do. Thank you so so so much :)
---------------------------------------------------

Answer. The lower tower is 40 m height. The higher tower is 90 m height.

Solution 

  

  
The scheme is shown in the Figure to the right.
The vertical lines AE and BF represent the towers.
The angle ECF formed by green lines is the right angle.                        


Due to this reason, the triangles ACE and BFC are similar 
  (and their respective vertices are listed in an corresponding order).

From the triangles similarity, we have a proportion 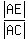abs%28AE%29%2Fabs%28AC%29 = abs%28BC%29%2Fabs%28BF%29, or 
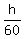h%2F60 = 60%2FH.   (1)

In addition to it, from the condition we have these equalities:

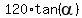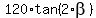h = 120%2Atan%28beta%29  and  H = 120%2Atan%28alpha%29 = 120%2Atan%282%2Abeta%29.      (2)
 
  

 
 




Substituting (2) into (1) we get this equation: 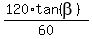 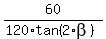%28120%2Atan%28beta%29%29%2F60 = 60%2F%28120%2Atan%282%2Abeta%29%29. 

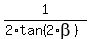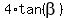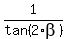After canceling by 60, you will get 2%2Atan%28beta%29 = 1%2F%282%2Atan%282%2Abeta%29%29,  or  4%2Atan%28beta%29 = 1%2Ftan%282%2Abeta%29.   (3)

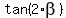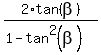Replacing here tan%282%2Abeta%29 = 2%2Atan%28beta%29%2F%281-tan%5E2%28beta%29%29,  you will get the equation

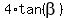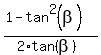4%2Atan%28beta%29 = %281-tan%5E2%28beta%29%29%2F%282%2Atan%28beta%29%29.  (4)

To solve it, introduce new variable x = 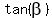tan%28beta%29.  You will get 

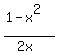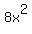4x = %281-x%5E2%29%2F%282x%29  --->  8x%5E2 = 1+-+x%5E2  --->  9x%5E2 = 1  --->  x = 1%2F3.

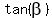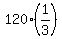Thus  tan%28beta%29 = 1%2F3,  and you just have   h = 120%2Atan%28beta%29 = 120%2A%281%2F3%29 = 40 m.

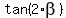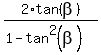Next, tan%282%2Abeta%29 = 2%2Atan%28beta%29%2F%281-tan%5E2%28beta%29%29 = . . . = 3%2F4,  and you finally get 

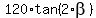H = 120%2Atan%282%2Abeta%29 = 120%2A%283%2F4%29 = 90 m.