SOLUTION: SOLVE THE EQUATION SIN3X=SINX

Algebra ->  Trigonometry-basics -> SOLUTION: SOLVE THE EQUATION SIN3X=SINX      Log On


   

Question 1005843: SOLVE THE EQUATION SIN3X=SINX
Answer by ikleyn(52794) About Me  (Show Source):
You can put this solution on YOUR website!
.
SOLVE THE EQUATION SIN3X=SINX
------------------------------- 
Start with the formula of triple argument for sine:

sin(3x) = -4*sin^3(x) + 3*sin(x)

(see,  for example,  the lesson  Trigonometric functions of multiply argument  in this site).

It gives you an equation 

-4*sin^3(x) + 3*sin(x) = sin(x).

Move the term sin(x) from the right side to the left with the opposite sign and then simplify.

-4*sin^3(x) + 3*sin(x) - sin(x) = 0,

-4*sin^3(x) + 2*sin(x) = 0.

Now factor the left side

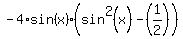-4%2Asin%28x%29%2A%28+sin%5E2%28x%29+-+%281%2F2%29+%29 = 0.   (1)

In this way the equation (1) decomposes in two equations. One is

sin(x) = 0 with the solutions x = 0, +/-pi, +/-2pi, +/-3pi, . . . , +/-k%2Api, . . . (2)

The other equation is 

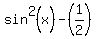+sin%5E2%28x%29+-+%281%2F2%29 = 0,   or

sin(x) = +/- sqrt%282%29%2F2.          

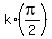It has the roots x = +/- k%2A%28pi%2F2%29.   (3)

So, the answer is the combination (the union) of solutions (2) and (3).

x = +/- {k*pi}}}, k = 0, 1, 2, 3, . . .  and

x = +/- 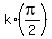k%2A%28pi%2F2%29, k = 0, 1, 2, 3, . . . 

Obviously, the last set overlay the previous one, so you may restrict yourself by the last formula.