Question 577996: Given a triangle with two altitudes having heights  and and  , I want to find the range of values for the third. , I want to find the range of values for the third.
I know that the formula is ( , ,  ) where ) where  , but where does this come from? , but where does this come from?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I never saw that formula before, but it should be  for the formula as written (Otherwise for the formula as written (Otherwise 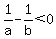 ). ).
I imagine that the formula comes from the fact that a side of a triangle must be less than the sum of the other two, but more than their difference. (Otherwise the side would be too long or too short to close the triangle).
Let's say that the lengths of the sides of a triangle are A, B, and C, with the corresponding altitudes a, b, and c respectively.
The area of the triangle, X, cam be calculated from the lengths of any side, taken as base, and the corresponding altitude.

If we knew the area and the height (length of the altitude), we could calculate the length of the side acting as base, so
 , ,  , and , and . .
We know about C that
 where where 
Substituting the expressions found before for A, B, and C,
 where where  <--> <-->  <--> <--> 
Multiplying all three sides of the triple inequality by 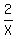 , it simplifies to , it simplifies to

Since the greater the number, the lesser the reciprocal, taking reciprocals we get to
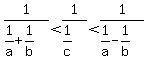 --> --> 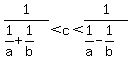 with with 
|
|
|