SOLUTION: How many different isosceles triangles have integer side lengths and a perimeter of 81 units?

Let's determine first what the largest possible measure each of 
the two congruent legs can have:

The smallest the base can be is 1, so the two congruent legs
would have length 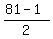 or 40 units each

Now we will determine what the smallest possible measure each of 
the two congruent legs can have:

If the two legs are "a" units each and the base is c, then by the
triangle inequality:

(1)                2a > c
 
and since the perimeter = 81 = a + a + c, 

               2a + c = 81

(2)                 c = 81 - 2a

Substitute the 81 - 2a for c in equation (1)

                   2a > c

                   2a > 81 - 2a

                   4a > 81

                    a >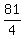 

                    a > 

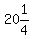Therefore the smallest "a" can be is 21

So "a" can range from 21 to 40, inclusive.

There are 40 integers from 1 to 40, and 20 of those are smaller than 21.

So there are 40-20 or 20 possible triangles.  Here they all are:

                  
1. sides 21, 21, 39
2. sides 22, 22, 37
3. sides 23, 23, 35
4. sides 24, 24, 33
5. sides 25, 25, 31
6. sides 26, 26, 29
7. sides 27, 27, 27
8. sides 28, 28, 25
9. sides 29, 29, 23
10. sides 30, 30, 21
11. sides 31, 31, 19
12. sides 32, 32, 17
13. sides 33, 33, 15
14. sides 34, 34, 13
15. sides 35, 35, 11
16. sides 36, 36, 9
17. sides 37, 37, 7
18. sides 38, 38, 5
19. sides 39, 39, 3
20. sides 40, 40, 1

Edwin