Question 175125This question is from textbook
: Find the center of the circle that you can circumscribe about triangle ABC.
A (0,0)
B (3,0)
C (3,2)
This question is from textbook
Answer by gonzo(654)   (Show Source): (Show Source):
You can put this solution on YOUR website! you have 3 points that are on the circumference of the circle.
you need to solve for the center of the circle using those points.
you do this as follows:
---
general form of the equation for a circle is:
(x-h)^2 + (y-k)^2 = r^2
where:
r is the radius of the circle.
(h,k) is the center of the circle.
---
using the 3 known points on the circle, you have 3 equations that have to be solved simultaneously.
they are:
using point A (0,0):> (0-h)^2 + (0-k)^2 = r^2 (first equation)
using point B (3,0):> (3-h)^2 + (0-k)^2 = r^2 (second equation)
using point C (3,2):> (3-h)^2 + (2-k)^2 = r^2 (third equation)
---
subtract the first equation from the second equation, and subtract the first equation from the third equation to eliminate the r^2 (r^2 - 4^2 = 0) from them and you will be left with 2 equations in 2 unknowns.
-----
some preliminary mathematics:
(0-h)^2 = h^2
(0-k)^2 = k^2
(3-h)^2 = 9 - 6h + h^2
(2-k)^2 = 4 - 4k + k^2
---
second equation minus first equation yields:
9 - 6h = 0
third equation minus first equation yields:
9 - 6h + 4 - 4k = 0
which equals:
13 - 6h - 4k = 0
---
9 - 6h = 0 yields h = 3/2
---
13 - 6h - 4k = 0 becomes 13 - 6*(3/2) - 4k = 0 when you substitute 3/2 for h.
this becomes 13 - 18/2 - 4k = 0 which becomes 13 - 9 - 4k = 0 which becomes:
4 - 4k = 0 which yields:
k = 1
---
you have:
h = 3/2
k = 1
center of circle = (h,k) = (3/2,1)
---
equation of circle is:
(x-h)^2 + (y-k)^2 = r^2
which becomes:
(x-3/2)^2 + (y-1)^2 = r^2
---
graph of this circle looks like this:
note:
in order to graph this equation, you have to solve for y.
the transformed equation is:
y = + or - 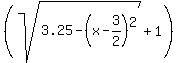 . .
you need to use both equations to draw the circle properly. ignore the gaps between the upper half and the lower half of the circle. the circumference of the circle is not really broken. it just shows up that way.
---
the 3 points of the triangle are on the circumference of the circle which means that the circle is circumscribing the triangle created by those 3 points.

|
|
|