Question 1209435: Equilateral triangle ABC with sides of 1cm has altitude AD. median AE of triangle ABD is drawn. What is the area, in cm^2, of triangle AEC?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52800)   (Show Source):
You can put this solution on YOUR website! .
Equilateral triangle ABC with sides of 1cm has altitude AD. median AE
of triangle ABD is drawn. What is the area, in cm^2, of triangle AEC?
~~~~~~~~~~~~~~~~~~~~~~
The area of the triangle ABC is 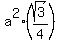 =  cm^2.
Every student, who studied the areas of triangles and the areas of equilateral
triangles, must know it, so I will not go in further explanations.
Next, when we draw altitude AD, we cut the area of triangle ABC in two equal half.
When we draw median AE in triangle ABD, we cut the area of triangle ABD in two equal parts.
Thus finally, the area of triangle AEC is 1 -  =  of the area of triangle ABC, i.e.  cm^2.
ANSWER. The area of triangle AEC is cm^2.
Solved.
--------------------
Actually, this problem is for / (or is from) mathematical mental competition,
where the answer should be given in the next instance to win.
I am absolutely serious: the true meaning of this question is that
it should be answered mentally quicker than you blink your eye.
Answer by math_tutor2020(3817)  (Show Source):
|
|
|
