SOLUTION: 20 triangles measuring 3 x 6 assemble into a square

20 RIGHT triangles with legs measuring 3 and 6 can be 
assembled into a square this way.

Let's calculate the length of the hypotenuse of each
of those right triangles using the Pythagorean theorem.

c² = a² + b²
c² = 3² + 6²
c² = 9 + 36
c² = 45
c = 
c = 
c = 

Each of the 20 right triangle has an area calculated by

A = bh = (3)(6) = 9 square units

The area of the square must be 20 times as much as
the area of one triangle, or 9x20 or 180 square units.

We can now calculate the side of the square by using the
formula for the area of a square,

A =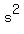  
180 =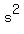 
Taking square roots of both sides,
 = 
 = 
 = 

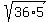Therefore each side of the square, being
, is twice the hypotenuse of
each triangle, which is .

Let's draw that square:



So we place two triangles on each side, 8
triangles in all, with their hypotenuses 
along the side of a square like this:  



Then draw 4 more line segments, making a smaller square
in the middle of the big square, and 4 rectangles
around it like this:



Notice that the square in the middle is a 6x6
square and the 4 rectangles around it are 3x6
rectangles.

Now we can split the 6x6 square into 2 3x6 rectangles,
like this:



Now we have 6 3x6 rectangles each of which can be split 
into 2 right triangles with legs 3 and 6, by drawing in a 
diagonal of each, like this:



That's it!  Count the rectangles.  They're 20 of them.

Edwin