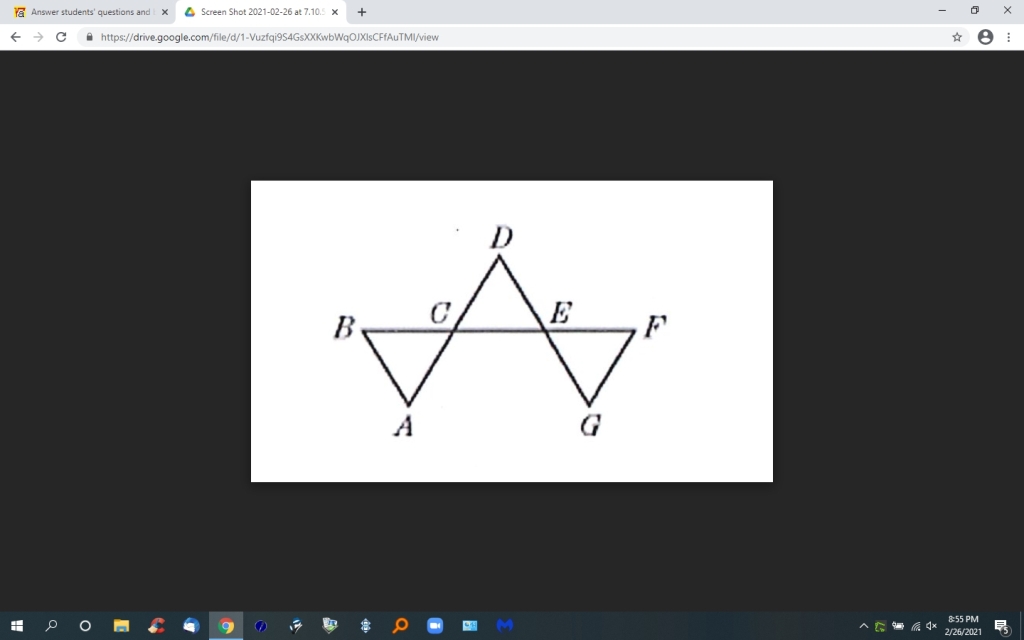
Question 1175958: In the diagram, AB || DG and AD || FG. If AB = 3, BC = 2, AC = 4, CE = 4, and EF = 5, what is the sum of the measures of the sides of the triangles? Express your answer as a common fraction.
My thoughts, the once that are parallel are equal to each other, so I think the total will be 1/6.
Please correct me
Link to the diagram - https://drive.google.com/file/d/1-Vuzfqi9S4GsXXKwbWqOJXlsCFfAuTMl/view?usp=sharing
Found 2 solutions by greenestamps, Theo:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
It's a little more complicated than that. And the answer you show ("1/6") makes no sense....
With the two sets of parallel segments, the figure consists of three similar triangles: ABC, DEC, and GFE.
For triangles ABC and DEC, BC and CE are corresponding parts; given BC=2 and CE=4. the ratio of similarity between those two triangles is 1:2. That makes DC = 2*AC = 8 and DE = 2*AB = 6.
In triangles DEC and GFE, CE and EF are corresponding parts, so the ratio of similarity between those two triangles is 4:5. Use that ratio to determine the lengths of side EG and FG. I leave that much of the problem to you.
Then of course remember that the question that is asked is the sum of the lengths of the sides of all three triangles.
Note the given figure is not at all to scale. Solving the problem will be easier if you draw a diagram of your own that depicts the figure more accurately. Start with triangle ABC, for which all side lengths are given; then use the defined parallel segments to complete the drawing.
Answer by Theo(13342)   (Show Source): (Show Source):
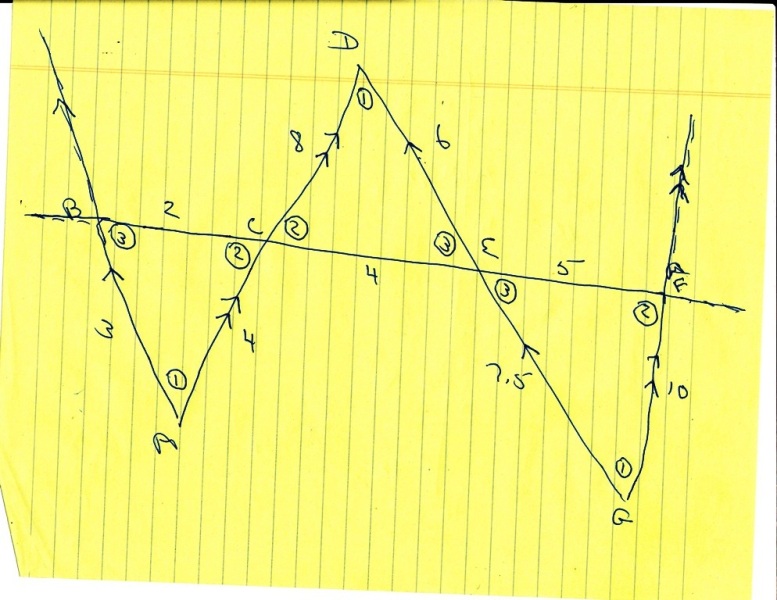
You can put this solution on YOUR website! here's the deal.
AD is parallel to FG.
this makes angle GFE equal to angle DCE because they are alternate interior angles to those two parallel lines.
those angles are labeled as 2 in my diagram.
also angle FGE is equal to angle EDC because they are alternate interior angles to the same two parallel lines.
those angles are labeled as 1 in my diagram.
AB is parallel to DG.
this makes angles BAC equal to angle CDE because they are alternate interior angles to those two parallel lines.
those angles are labeled 1 in my diagram.
also angle CBA is equal to angle DEC because they are alternate interior angles to those two parallel lines.
those angles are labeled 3 in my diagram.
you also have angle BCA = angle DCE because they are vertical angles to each other.
those two angles are labeled 2 in my diagram.
you also have angle DEC equal to angle GEF because they are vertical angles to each other.
those two angles are labeled 3 in my diagram.
the bottom line is that triangles ABC and DEC and GEF are all similar to each other because their angles are equal.
since they are similar to each other, their sides are proportional.
the ratio from triangle DEC to ABC is 2/1.
the ratio from triangle GEF to ABC is 5/2.
the ratio from triangle GEF to DEC is 5/4.
this means that corresponding sides of these triangle will have the same ratio to each other.
to find the corresponding sides, you look for the sides opposite the angles that are equal to each other.
example:
BC is opposite angle 1 in its triangle and CE is opposite angle 1 in its triangle.
the ratio between those two triangle is 2/1, so if BC is 2 then CE is 4.
this was one of the givens and was used to get the ratio for the other sides.
since AB was 3 and is opposite angle 2 in its triangle, then DE is 6 because it is opposite angle 2 in its triangle.
likewise angle 1 from triangle ABC is equal to angle 1 from triangle GEF.
the side opposite angle 1 in triangle ABE is equal to 2 and the side opposite angle 1 in triangle GEF is equal to 5.
this sets the ratio of the sides as 5/2 from triangle GEF to ABC.
likewise the side opposite angle 1 in triangle DEC is equal to 4 and the side opposite angle 1 in triangle GEF is equal to 5.
this sets the ratio of sides as 5/4 from triangle GEF to DEC.
you use those ratios to get the rest of the corresponding sides of each triangle.
now that you know what all the sides measure, you can get their sum.
you can add each one up individually to get a sum of 49.5
or, .....
you can sum up the sides of triangle ABC to get 9.
since the ratio of triangle DEC to ABC is 2 to 1, then the sum for triangle DEC is 2/1 * 9 = 18.
since the ratio of triangle GEF to ABC is 5/2,then the sum for triangle GEF is 5/2 * 9 = 22.5
9 + 18 + 22.5 = 49.5.
same answer.
here's my diagram.
note that the transversals to parallel lines AB and DG are AD and BE.
note also that the transversals to parallel lines AD and GF are DG and CF.
here's my diagram and yours below it.
|
|
|