Question 1133010: In how many ways can we form a nondegenerate triangle by choosing three distinct numbers from the set {1,2,3,4,5} as the sides?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
There are 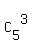 =  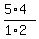= 10 ways to choose 3 distinct numbers of given 5 numbers.
It is not astronomically large number, and I can list all 10 combinations in the list below:
1) 1 2 3 (3 = 1 + 2, degenerate)
2) 1 2 4 (4 > 1 + 2, impossible)
3) 1 2 5 (5 > 1 + 2, impossible)
4) 1 3 4 (4 = 1 + 3, degenerate)
5) 1 3 5 (5 > 1 + 3, impossible)
6) 1 4 5 (5 = 1 + 4, degenerate)
7) 2 3 4
8) 2 3 5 (5 = 2 + 3, degenerate)
9) 2 4 5
10) 3 4 5
In the next column on the right, I commented each combination/configuration.
"degenerate" means degenerated triangle.
"impossible" means a case where the triangle inequality is violated.
Empty comment means "a triangle is possible".
From the table, there are only 3 possible triangles ## 7, 9 and 10. ANSWER
Solved.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
If 1 were the shortest side, then the other two sides would have to have lengths whose difference is less than 1. Since we can only choose integer values, this is not possible.
So there are no triangles with shortest side 1.
If 2 is the shortest side, then the difference between the lengths of the other two sides must be less than 2. Since we can only choose integer values, the difference between the lengths of the other two sides must be 1. So there are 2 triangles with shortest side 2: 2-3-4 and 2-4-5.
If 3 is the shortest side, then the other two sides have to be 4 and 5.
ANSWER: 3 triangles: 2-3-4, 2-4-5, and 3-4-5.
|
|
|
