Question 1089361: Find the range of possible measures of x if each set of expressions represents measures of the sides of a triangle.
x+2,x+4,x+6
Thank you very much. God bless you.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Obviously, 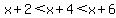 , because , because 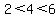 . .
If  , ,  , and , and 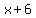
are the lengths of the side of a triangle,
they should all be positive values,
and for that it is enough to require that 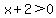 ---> --->  . .
You know that
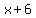 is the length of the longest side. is the length of the longest side.
You would also know that the length of the longest side
must be less than the sum of the lengths of the other two sides.
That means
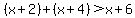 , ,
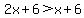 , ,
and subtracting x and 6 from both sides,
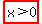 . .
That shows you the range of possible measures for x.
In interval notation, it would be 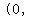   . .
That is all that is required for x.
EXPLANATIONS AND MORE:
As long as  , you could draw such a triangle. , you could draw such a triangle.
With  , all three expressions given have positive values, , all three expressions given have positive values,
and knowing their values you could easily build a triangle with two sides measuring  and and  . .
You could just start by drawing those sides as segments AB and AC,
connected at A, forming any angle BAC, like this

Then, all you would have to do is draw a third side, by connecting points B and C with a straight line.
The distance along that straight segment BC would have be shorter than the sum of the length of the other two sides,
but making angle BAC smaller or larger,
you could give the third side any positive length smaller than 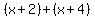 . .
A straight line is the shorter distance between two points, such as B and C.
Common sense tells you that.
A geometry teacher tells you that the length of a side of a triangle is less that the sum of the lengths of the other two sides.
Drawing a triangle, with specified measures for only two of the sides is easy.
If the lengths of all three sides are specified,
it may be possible to draw/construct a triangle to meet the reasonable specifications,
but it may require either knowledge of geometry constructions,
or the common sense a carpenter or gardener would have.
How would you do it in geometry class?
How would you do it as a gardener?
|
|
|