Question 1066301: AB is the diameter of a circle. AD and BC are tangents to the circle with AD = 9cm and BC = 16cm. If AC and BD intersect at a point on the circle, then the length, in centimetres, of AB is:
a) 5.76 cm b) 9 cm c) 12 cm d) 12.5 cm e) 25 cm
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
AB is the diameter of a circle. AD and BC are tangents to the circle with AD = 9cm and BC = 16cm.
If AC and BD intersect at a point on the circle, then the length, in centimetres, of AB is:
a) 5.76 cm b) 9 cm c) 12 cm d) 12.5 cm e) 25 cm
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
0. Make a sketch.
Let "x" be the length of AB, which is under the question: x = |AB|.
1. Let P be the intersection point of the segments AC and BD.
As the condition says, the point P lies on the circle.
Therefore, the angle APB is the right angle (it leans on the diameter AB !)
Thus, the segments AC and BD are perpendicular.
Also, let's denote a = |BP|, b = |AP|.
2. Right-angled triangles ABC and APB are similar (they have the common acute angle BAP).
Therefore, their corresponding sides are proportional:  = =  , or , or 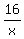 = = 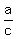 . (1)
3. Right-angled triangles BAD and BPA are similar (they have the common acute angle ABP).
Therefore, their corresponding sides are proportional: . (1)
3. Right-angled triangles BAD and BPA are similar (they have the common acute angle ABP).
Therefore, their corresponding sides are proportional:  = = 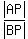 , or , or  = =  . (2)
4. Divide (1) by (2) (both sides). You will get . (2)
4. Divide (1) by (2) (both sides). You will get 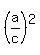 = =  , which implies , which implies 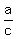 = = 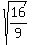 = =  .
5. Now substitute .
5. Now substitute  instead of instead of 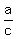 into (1).
You will get into (1).
You will get 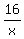 = =  , which implies x = , which implies x =  = 12. = 12.
Answer. |AB| = 12 cm. Option c).
|
|
|