Question 1036188: Find Height of the statue of liberty's body.
Found 2 solutions by Cromlix, MathTherapy:
Answer by Cromlix(4381)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi there,
First you have to annotate the triangles.
The main one, the base of which is to the
base of the statue. The upright is equal to 305 ft.
The hypotenuse is from the boat to the head of the
statue.
We will call this triangle ABC
A is at the boat, B is at the base of the statue and
C is at the head of the statue.
As Angle C = 60 degrees, then Angle B is = 90 degrees
and Angle C = 180 - (90 + 60) = 30 degrees.
Using Pythagoras, we can calculate the hypotenuse(AC)
Sin(60) = CB/AC
Sin(60) = 305/AC
Cross multiply
Sin(60) AC = 305
AC = 305/Sin(60)
AC = 352.2 feet (1 decimal place)
Now we consider the top triangle.
this we will call ADC. D being at the statue's
feet. DC = 'h'
.............
Considering triangle ADC.
Now Angle A = (60 - 41.2) = 18.8 degrees
Angle C = 30 degrees
So, Angle D = 180 - (30 + 18.8) = 131.2 degrees.
We now use Sine Rule:
namely a/SinA = c/SinC = d/SinD (For this triangle)
Using a/SinA = d/SinD
a/Sin(18.8) = 305.2/Sin(131.2)
Cross multiply:
a x sin(131.2) = 305.2 x sin(18.8)
a = (305.2 x sin(18.8))/sin(131.2)
a = 130.7 feet (1 decimal place)
This is the height of 'h'
the statue's height.
Hope this helps :-)
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Since the entire structure represents a 30-60-90 special triangle, the distance from the boat to the base of the statue (also the SHORTER leg of the triangular structure) is: 
Using 305 - h as the height of the statue's base, the shorter leg:  , the angle of elevation , the angle of elevation 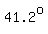 from the boat to the base of the statue, we get h, or height of statue as: from the boat to the base of the statue, we get h, or height of statue as: 
Different approach
The hypotenuse (distance from boat to top of statue) can be derived. As this is a 30-60-90 special right triangle, the hypotenuse is: 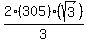 , or , or 
Difference between angles of elevation: 60 - 41.2, or 
Using height of statue only (h), difference in angles of elevation ( ), the hypotenuse: ), the hypotenuse:  , the third angle in that triangle ( , the third angle in that triangle (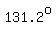 ), and the law of sines, we get: ), and the law of sines, we get: 
 ------- Cross-multiplying ------- Cross-multiplying
h, or height of statue = 
|
|
|