Question 1027075: Find the length of the shortest altitude of a triangle with sides of lengths 10, 24, and 26.
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52786)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the length of the shortest altitude of a triangle with sides of lengths 10, 24, and 26.
You have to 1st determine the area of the triangle.
This triangle represents a Pythagorean triple (10-24-26, or 5-12-13), which means that it's a right triangle. No sweat!
Using the 2 legs, you can find the area by applying the formula for the area of a triangle:  , which results in: , which results in: 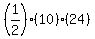 , ,
for an area of 120 sq units. Now, if this were NOT a right triangle, the easiest method to find the area is Heron's formula.
Now that we have the area, the shortest altitude, of the three, is the altitude that's drawn to the longest side,
which in this case is the hypotenuse. After drawing the shortest altitude to the hypotenuse, we now apply the formula
for the area of a triangle, once again, but this time, the base is the hypotenuse, and the altitude (shortest) is unknown.
This gives us: 


h, or shortest altitude to this triangle = 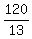 , or , or 
|
|
|