Question 1001212: D is a point on side BC of a triangle ABC such that A is perpendicular on BC. E is a point on AD for which AE:ED = 5:1.If angle BAD =30 and tan(angle ACB)=6tan(angle DBE),Find angle ACB.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I am assuming the problem states that:
D is a point on side BC of a triangle ABC such that AD is perpendicular to BC.
E is a point on AD for which AE:ED = 5:1.
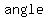 

In that case, the triangle looks like this:
 Triangles ACD, ABD, and EBD are right triangles, each of them having a right angle at vertex D. Triangles ACD, ABD, and EBD are right triangles, each of them having a right angle at vertex D.
In triangle ABD,
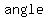  , so , so 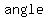  . .
In triangle EBD,
 . .
In triangle EBD,
 . .
 ---> ---> ---> ---> . .
So right triangles ABD and ACD are congruent,
meaning that angles  and and  are congruent. are congruent.
Since 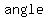  , , 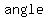 
|
|
|