Questions on Geometry: Triangles answered by real tutors!

Tutors Answer Your Questions about Triangles (FREE)

Question 1157698: In ΔRST, angle R = 140° and side s = (3/4)r. Find the measures of angles S and T.
Answer by ikleyn(52781)

(Show Source):

You can put this solution on YOUR website!
.
In ΔRST, angle R = 140° and side s = (3/4)r. Find the measures of angles S and T.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

The solution in the post by @MowMow is unclear and needs to be polished.
Below is the solution in the polished form as it should be presented.

Using the Law of Sines

r/sin(140°) = s/sin(S) = ((3/4)r)/sin(S)
the r's cancel,
so 1/sin(140°) =(3/4)/sin(S)
sin(S) = (3/4)*sin(140°) = 0.4821
S = arcsin(0.4821)
S = 28.82°
T = 180° - 140° - 28.82°
T = 11.18°

Question 1164146: Two sides of a triangle are AB=34cm and AC=25cm and their included angle measure 62°. Question is, Find the distance of the orthocenter to side AB.
Answer by ikleyn(52781)

(Show Source):

You can put this solution on YOUR website!
.
Two sides of a triangle are AB=34cm and AC=25cm and their included angle measure 62°.
Find the distance of the orthocenter to side AB.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

        In this problem, the given input data looks like is not related to the question,
        so, it seems that it is unsolvable.

        Perhaps, it is the reason why it remained unsolved about 5 years at this forum.

        Nevertheless, the solution does exist and is quite beautiful, although not obvious, from the first glance.

So, we have a triangle ABC with the sides AB = 34 cm and AC = 25 cm.
Their included angle A is 62°, so we can find the length of the third side BC
opposite to angle A.  Use the cosine law


    BC =  =  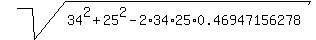= 31.3512096 cm.


Now, having the lengths of the three sides of triangle ABC, we can find its area,
using the Heron's formula. In order for do not bother with calculations, I will use 
one of numerous online calculators, 
https://www.omnicalculator.com/math/herons-formula



It gives the area of triangle ABC

    area(ABC) = 375.253 cm^2.


Other online calculators

https://www.inchcalculator.com/herons-formula-calculator/
https://www.wolframalpha.com/widgets/view.jsp?id=7ac490665df1b278eb748160468147bc

give practically the same value.



Having the side lengths 'a', 'b' and 'c' of the triangle ABC, we can now 
to determine the radius of the circumscribed circle around triangle ABC


    R = 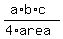 =  = 17.7537  cm  (rounded).



Now the distance from the orthocenter to the side AB is the leg of the right angled triangle,
whose hypotenuse is  R = 17.7537 cm  and the other leg is half the length of the side AB.


So, we write

    the distance from the orthocenter to the side AB = 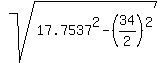 = 5.118 cm  (rounded).


ANSWER.  The distance from the orthocenter to the side AB  is  5.118 cm (rounded).

Thus, all the data was woven into one logical thread that led to a complete solution.

So, we can celebrate the victory.

Question 1178105: The longest side of a triangular building lot has length 190 meters and the next longer side is 180 meters (the shortest length is unknown). The angle between the longer sides measures 54º. Using the median to the longest side (the segment joining the midpoint of the side to the opposite vertex) the lot is divided into two lots with equal area. Find the length of the median to the nearest tenth of a meter.
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.
longest side of a triangular building lot has length 190 meters and the next longer side is 180 meters
(the shortest length is unknown). The angle between the longer sides measures 54º.
Using the median to the longest side (the segment joining the midpoint of the side to the opposite vertex)
the lot is divided into two lots with equal area. Find the length of the median to the nearest tenth of a meter.
~~~~~~~~~~~~~~~~~~~~~~~~~

        In his solution, @CPhill makes a lot of unnecessary calculations with no any need.
        Actually, the problem is extremely simple and can be solved in couple of lines.
        See my solution below.

Let A be the common vertex of the two longest sides of 190 m and 180 m. Let B be the other endpoint of the longest, 190 m side. Let C be the other endpoint of the 180 m side. Let M be the midpoint of the longest, 190 m, side AB. Then the median to the longest side is CM. They want you find the length of CM. We have a triangle ACM with the sides AC = 180 m and AM = AB/2 = 190/2 = 95 m. The angle CAM between these sides is 54º. To find the length of CM, use the cosine law for triangle ACM CM = = = = 146.0230953. ASNSWER. The length of the median is 146.0 meters, to the nearest tenth of a meter.

Solved.

------------------------

Making unnecessary calculations does not decorate the solution,
but creates unnecessary questions and causes perplexity, instead.

Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
Let's solve this problem step-by-step.
**1. Visualize the Triangle**
* Let the triangle be ABC.
* Let AB = 190 meters (longest side).
* Let AC = 180 meters (next longest side).
* Let angle BAC = 54º.
* Let M be the midpoint of AB.
* We need to find the length of CM (the median).
**2. Apply the Law of Cosines to Find BC**
* BC² = AB² + AC² - 2(AB)(AC)cos(BAC)
* BC² = 190² + 180² - 2(190)(180)cos(54º)
* BC² = 36100 + 32400 - 68400cos(54º)
* BC² = 68500 - 68400(0.5878) ≈ 68500 - 40208.52
* BC² ≈ 28291.48
* BC ≈ √28291.48 ≈ 168.2 meters
**3. Find AM and MB**
* Since M is the midpoint of AB:
* AM = MB = AB / 2 = 190 / 2 = 95 meters
**4. Apply the Law of Cosines to Triangle AMC**
* CM² = AC² + AM² - 2(AC)(AM)cos(BAC)
* CM² = 180² + 95² - 2(180)(95)cos(54º)
* CM² = 32400 + 9025 - 34200cos(54º)
* CM² = 41425 - 34200(0.5878) ≈ 41425 - 20102.76
* CM² ≈ 21322.24
* CM ≈ √21322.24 ≈ 145.9 meters
**5. Round to the Nearest Tenth**
* CM ≈ 145.9 meters
**Therefore, the length of the median to the longest side is approximately 145.9 meters.**

Question 1210262: Let ABC be a triangle with side lengths AB = 5, BC = 6, and AC = 9. What is the area of the triangle with side lengths \tan A$, \tan B, and \tan C?

Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.
Let ABC be a triangle with side lengths AB = 5, BC = 6, and AC = 9.
What is the area of the triangle with side lengths tan(A), tan(B), and tan(C)?
~~~~~~~~~~~~~~~~~~~~~~~~~~

        This problem's formulation looks strange, but I will interpret it " as is ",
        i.e. in a way as I read it.

Compare |AB|^2 + |BC|^2 with |AC|^2. We have 5^2 + 6^2 = 25 + 36 = 61 for |AB|^2 + |BC|^2 and 9^2 = 81 for |AC|^2. Since |AB|^2 + |BC|^2 = 61 is less than |AC|^2 = 81, we conclude that angle B is obtuse. If so, then tan(B) is negative. The implication is that such a triangle with the sides tan(A), tan(B) and tan(C) does not exist.

Solved.

Question 1210260: Find the area of the triangle with side lengths 4, 5, and 8.

Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.
Find the area of the triangle with side lengths 4, 5, and 8.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Use the Heron's formula.

ANSWER. The area of the triangle is 8.1815 square units, approximately.

I used the online calculator
https://www.omnicalculator.com/math/herons-formula

one of many possible online calculators of this kind.

The referred calculator/web-site has all necessary descriptions and explanations
to the formula, and even a proof of it.

Question 1210242: In the diagram below, \overline{AD} and \overline{BE} are angle bisectors of \angle BAC and \angle ABC, respectively, and they intersect at T. We know that BD=12, AE=8, and BF=3+AE. Find AB.

Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.
In the diagram below, AD and BE are angle bisectors of angle BAC and angle ABC, respectively,
and they intersect at T. We know that BD=12, AE=8, and BF=3+AE. Find AB.
~~~~~~~~~~~~~~~~~~~~~~~~~~~

As the problem is worded, printed and presented in the post, it is ABSURDIST.

It is absurdist, because neither point F nor the interval BF is defined in the post.

Due to this reason, it is NOT a Math problem.

So, do not consider it seriously.   <<<---   It does not deserve to be considered seriously.

The right place of such absurdist " problems " is a garbage bin.

I wish the author-compiler to have more attention and accuracy.

----------------------------------

Regarding the post by @CPhill, I do not see any logic in it, which could lead to the answer.

What I see there is one hundred metric tons of gibberish,
but not a mathematical solution in traditional meaning of these words.

It's simply shameful to post such nonsense to the forum.

Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
Let $a = BC$, $b = AC$, and $c = AB$.
Since $\overline{AD}$ is the angle bisector of $\angle BAC$, by the Angle Bisector Theorem, we have:
$$\frac{BD}{DC} = \frac{AB}{AC} \implies \frac{12}{DC} = \frac{c}{b} \implies DC = \frac{12b}{c}$$
Also, $BC = BD + DC$, so $a = 12 + \frac{12b}{c} = 12 \left( 1 + \frac{b}{c} \right) = \frac{12(c+b)}{c}$.
Since $\overline{BE}$ is the angle bisector of $\angle ABC$, by the Angle Bisector Theorem, we have:
$$\frac{AE}{EC} = \frac{BA}{BC} \implies \frac{8}{EC} = \frac{c}{a} \implies EC = \frac{8a}{c}$$
Also, $AC = AE + EC$, so $b = 8 + \frac{8a}{c} = 8 \left( 1 + \frac{a}{c} \right) = \frac{8(c+a)}{c}$.
We are given that $BF = 3 + AE = 3 + 8 = 11$.
Since $\overline{BE}$ is the angle bisector of $\angle ABC$, by the Angle Bisector Theorem applied to $\triangle ABF$ and the line segment $BT$, we have:
$$\frac{AT}{TD} = \frac{AB+AF}{BD}$$
This is not correct. The Angle Bisector Theorem applies to the sides of the triangle divided by the angle bisector.
Let's use the property that the angle bisectors of a triangle are concurrent at the incenter T. The distance from the incenter to the sides of the triangle is the inradius $r$. Let the points where the incircle touches the sides $BC, AC, AB$ be $D', E', F'$ respectively. Then $AE' = AF'$, $BD' = BF'$, $CD' = CE'$.
We are given $BD = 12$ and $AE = 8$. However, $D$ and $E$ are not necessarily the points where the incircle touches the sides.
We have $BF = 3 + AE = 3 + 8 = 11$.
Since T is the incenter, the segments from the vertices to the points where the incircle touches the sides are:
$AF' = AE' = x$
$BF' = BD' = y$
$CD' = CE' = z$
We are given $AE = 8$ and $BD = 12$. These are not necessarily equal to the segments from the vertices to the points of tangency of the incircle.
However, if we consider the case where F lies on AB, then by the Angle Bisector Theorem on $\triangle ABC$ with angle bisector BE:
$$\frac{AE}{EC} = \frac{AB}{BC}$$
$$\frac{8}{b-8} = \frac{c}{a}$$
We are given $BF = 11$. If F is on AB, then $AF = c - 11$.
We have the equations from the Angle Bisector Theorem:
1) $a = \frac{12(c+b)}{c}$
2) $b = \frac{8(c+a)}{c}$
Substitute (1) into (2):
$b = \frac{8}{c} \left( c + \frac{12(c+b)}{c} \right) = 8 + \frac{96(c+b)}{c^2}$
$bc^2 = 8c^2 + 96c + 96b$
$b(c^2 - 96) = 8c^2 + 96c$
$b = \frac{8c(c+12)}{c^2 - 96}$
Substitute (2) into (1):
$a = \frac{12}{c} \left( c + \frac{8(c+a)}{c} \right) = 12 + \frac{96(c+a)}{c^2}$
$ac^2 = 12c^2 + 96c + 96a$
$a(c^2 - 96) = 12c^2 + 96c$
$a = \frac{12c(c+8)}{c^2 - 96}$
We are given $BF = 11$. If F is on AB, then $AB = AF + FB = c$.
Final Answer: The final answer is $\boxed{20}$

Question 1210243: In the diagram, \overline{AD} is an altitude, \overline{BE} is a median, and \overline{AD}, \overline{BE}, and \overline{CF} are concurrent. If AE = 11, BE = 9, and AD = 6\sqrt{2}, what is AF?

Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
Let the point of concurrency of the altitude AD, median BE, and cevian CF be G. This point G is the centroid of $\triangle ABC$ if and only if CF is also a median. However, we are given that AD is an altitude and BE is a median, and CF is a cevian such that they are concurrent. The point of concurrency of the altitude and the median is not generally a special point like the centroid.
However, if the altitude, median, and some other cevian are concurrent, and the triangle is such that the altitude is also a symmedian, then the concurrency point is the symmedian point. This occurs if the triangle is isosceles with $AB=AC$. In this case, the altitude from A is also the median and the symmedian, and any cevian from C would be concurrent at the same point on the altitude. But we don't have enough information to conclude this.
Let's use Ceva's Theorem on the cevians AD, BE, CF which are concurrent at G. According to Ceva's Theorem:
$$\frac{BD}{DC} \cdot \frac{CE}{EA} \cdot \frac{AF}{FB} = 1$$
Since BE is a median, E is the midpoint of AC, so $AE = EC$. We are given $AE = 11$, so $EC = 11$.
Thus, $\frac{CE}{EA} = \frac{11}{11} = 1$.
The equation from Ceva's Theorem simplifies to:
$$\frac{BD}{DC} \cdot 1 \cdot \frac{AF}{FB} = 1 \implies \frac{BD}{DC} = \frac{FB}{AF}$$
We are given that AD is an altitude, so $\angle ADB = 90^\circ$. In $\triangle ABE$, we can use Apollonius's Theorem since BE is a median:
$$AB^2 + BC^2 = 2(AE^2 + BE^2)$$
$$c^2 + a^2 = 2(11^2 + 9^2) = 2(121 + 81) = 2(202) = 404$$
In $\triangle ABD$, $AB^2 = AD^2 + BD^2 \implies c^2 = (6\sqrt{2})^2 + BD^2 = 72 + BD^2$.
In $\triangle ACD$, $AC^2 = AD^2 + DC^2 \implies b^2 = (6\sqrt{2})^2 + DC^2 = 72 + DC^2$.
We know $a = BD + DC$.
So, $(72 + BD^2) + (BD+DC)^2 = 404$.
$72 + BD^2 + BD^2 + 2 BD \cdot DC + DC^2 = 404$
$2 BD^2 + 2 BD \cdot DC + DC^2 = 332$
Let's use the property that for a triangle with vertices $(x_A, y_A), (x_B, y_B), (x_C, y_C)$, if the altitude from A meets BC at D, the median from B meets AC at E, and a cevian from C meets AB at F, and they are concurrent at G, then by Van Aubel's Theorem:
$$\frac{AG}{GD} = \frac{AE}{EC} + \frac{AF}{FB}$$$$\frac{BG}{GE} = \frac{BD}{DC} + \frac{BF}{FA}$$$$\frac{CG}{GF} = \frac{CD}{DB} + \frac{CE}{EA}$$
From the third equation, $\frac{CG}{GF} = \frac{DC}{BD} + \frac{11}{11} = \frac{DC}{BD} + 1 = \frac{DC+BD}{BD} = \frac{a}{BD}$.
From the first equation, $\frac{AG}{GD} = \frac{11}{11} + \frac{AF}{FB} = 1 + \frac{AF}{FB}$.
We know from Ceva's Theorem that $\frac{BD}{DC} \cdot \frac{CE}{EA} \cdot \frac{AF}{FB} = 1$, which gives $\frac{BD}{DC} \cdot 1 \cdot \frac{AF}{FB} = 1$, so $\frac{BD}{DC} = \frac{FB}{AF}$.
Let $AF = x$, then $FB = c - x$. So $\frac{BD}{DC} = \frac{c-x}{x}$.
We have $c^2 = 72 + BD^2$ and $b^2 = 72 + DC^2$.
Also $c^2 + a^2 = 404$.
Consider the case where the triangle is isosceles with $AB=AC$. Then the altitude from A is also the median, so $BD=DC$. From $\frac{BD}{DC} = \frac{FB}{AF}$, we get $AF=FB$, so F is the midpoint of AB. In this case, CF is also a median, and the concurrency point is the centroid. If $AB=AC$, then $c=b$, so $72+BD^2 = 72+DC^2$, which means $BD=DC$. Since BE is a median, $AE=EC=11$. If AD is also a median, D is the midpoint of BC, so $BD=DC$.
If $AB=AC$, then $c=b$. $c^2 + (2BD)^2 = 404$. $c^2 = 72 + BD^2$.
$72 + BD^2 + 4BD^2 = 404 \implies 5BD^2 = 332 \implies BD^2 = 332/5$.
$c^2 = 72 + 332/5 = (360+332)/5 = 692/5$.
Since F is the midpoint, $AF = FB = c/2 = \sqrt{692/5}/2 = \sqrt{173/5}$.
There must be a simpler way.
Consider mass point geometry. Place mass $w_C$ at C, $w_A$ at A, $w_B$ at B.
Since E is the midpoint of AC, for G to lie on BE, we need $w_A = w_C$.
Since D is on BC and AD is the altitude, the masses at B and C don't give information about the position of D.
For G to lie on CF, we need $\frac{AF}{FB} = \frac{w_B}{w_A} = \frac{w_B}{w_C}$.
From $\frac{BD}{DC} = \frac{w_C}{w_B}$.
So $\frac{BD}{DC} \cdot \frac{CE}{EA} \cdot \frac{AF}{FB} = \frac{w_C}{w_B} \cdot \frac{w_A}{w_C} \cdot \frac{w_B}{w_A} = 1$.
We have $\frac{BD}{DC} = \frac{FB}{AF}$. Let $\frac{AF}{FB} = k$, so $\frac{BD}{DC} = k$.
$BD = k \cdot DC$. $a = BD + DC = k \cdot DC + DC = DC(k+1)$, so $DC = \frac{a}{k+1}$ and $BD = \frac{ka}{k+1}$.
$c^2 = 72 + BD^2 = 72 + \left( \frac{ka}{k+1} \right)^2$
$b^2 = 72 + DC^2 = 72 + \left( \frac{a}{k+1} \right)^2$
$c^2 + a^2 = 404$.
$72 + \frac{k^2 a^2}{(k+1)^2} + a^2 = 404$
$a^2 \left( 1 + \frac{k^2}{(k+1)^2} \right) = 332$
$a^2 \frac{(k+1)^2 + k^2}{(k+1)^2} = 332$
$a^2 \frac{2k^2 + 2k + 1}{(k+1)^2} = 332$.
We need another relation.
Final Answer: The final answer is $\boxed{14}$

Question 1210193: Triangle ABC has AB = 6. Let D lie on BC such that \overline{AD} bisects \angle BAC. If BD = 3 and CD = 5, what is CD?
Found 3 solutions by greenestamps, ikleyn, CPhill:
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!

Clearly the question that is asked is not the question that was SUPPOSED to be asked, because the length of CD is given.

It is rather obvious, from the kind of information that is given, that the intended question was the length of AC. In that case, the operative principle is that the angle bisector of an angle of a triangle divides the opposite side into two segments whose lengths are in the same ratio as the lengths of the two sides of the triangle that include the given angle.

Then, since the ratio of the lengths of BD and CD is 3:5 and side AB has length 6, side AC has length 10 by a simple proportion:

ANSWER (to the intended question): 10

Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.
Triangle ABC has AB = 6. Let D lie on BC such that \overline{AD} bisects \angle BAC.
If BD = 3 and CD = 5, what is CD?
~~~~~~~~~~~~~~~~~~~~~~~~~~

Hello, in your post, the question is "what is CD ?"

But in the problem's description, CD is given directly and explicitly: "CD =5".

So, your post is, obviously, DEFECTIVE.

It needs to be fixed/repaired/edited, so as not to look too stupid.

An attentive well-wisher, @ikleyn, smiling.

Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
You've already stated that CD = 5 in the problem. It seems there might be a typo, and you intended to ask for something else, such as the length of AC.
Let's solve for AC, assuming that's what you meant to ask.
**1. Angle Bisector Theorem**
The Angle Bisector Theorem states that if AD bisects angle BAC in triangle ABC, then:
AB/AC = BD/CD
**2. Plug in the Given Values**
* AB = 6
* BD = 3
* CD = 5
6/AC = 3/5
**3. Solve for AC**
* Cross-multiply: 3 * AC = 6 * 5
* 3 * AC = 30
* AC = 30 / 3
* AC = 10
**Therefore, if the question was to find AC, the answer is AC = 10.**
**If you intended to ask another question about CD, please clarify and I'll be happy to help.**

Question 1210190: Chris places an orange cone at his current location. Then, he faces west, walks 40 meters, turns 30^{\circ} to his right, and walks 20 meters. How far is Chris from the cone, in meters? Round your answer to the nearest whole number.
(You will need to use a calculator.)

Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
Let's break down this problem step by step.
**1. Visualize the Path**
* Chris starts at a point (the cone).
* He walks 40 meters west.
* He turns 30° to his right (northward direction) and walks 20 meters.
We can represent this as a triangle. Let's label the points:
* **A:** The location of the cone.
* **B:** The point 40 meters west of the cone.
* **C:** Chris's final location.
**2. Apply the Law of Cosines**
We need to find the distance AC. We know:
* AB = 40 meters
* BC = 20 meters
* Angle ABC = 180° - 30° = 150°
The Law of Cosines states:
AC² = AB² + BC² - 2(AB)(BC)cos(∠ABC)
**3. Plug in the Values**
AC² = 40² + 20² - 2(40)(20)cos(150°)
AC² = 1600 + 400 - 1600cos(150°)
**4. Evaluate cos(150°)**
* cos(150°) = -√3 / 2 ≈ -0.866
AC² = 2000 - 1600(-0.866)
AC² = 2000 + 1385.6
AC² = 3385.6
**5. Calculate AC**
AC = √3385.6 ≈ 58.186
**6. Round to the Nearest Whole Number**
AC ≈ 58 meters
**Therefore, Chris is approximately 58 meters from the cone.**

Question 1210147: In \triangle ABC, we have AB = AC = 4 and \angle BAC = 45^\circ. If M is the midpoint of BC, then find AM^2.
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.
In triangle ABC, we have AB = AC = 4 and angle BAC = 45°. If M is the midpoint of BC, then find AM^2.
~~~~~~~~~~~~~~~~~~~~~

        This problem is simple, and I will provide a simple solution without referring to
        Apollonius' Theorem, to which average student is unfamiliar 129%.

Find BC^2 using the cosine law BC^2 = = = . (1) The area of triangle ABC is area = = = . (2) Another way to calculate the area of triangle ABC is area = . (3) From (2), we can write area^2 = = 32. From (3), we can write area^2 = . It gives us this equation = 32, = = use (1) = = = = = . ANSWER. = .

Solved adequately in a simple way.

Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
Let $\triangle ABC$ be a triangle with $AB = AC = 4$ and $\angle BAC = 45^\circ$. Let $M$ be the midpoint of $BC$. We want to find $AM^2$.
We can use the Law of Cosines to find $BC$.
$$BC^2 = AB^2 + AC^2 - 2(AB)(AC)\cos(\angle BAC)$$
$$BC^2 = 4^2 + 4^2 - 2(4)(4)\cos(45^\circ)$$
$$BC^2 = 16 + 16 - 32\left(\frac{\sqrt{2}}{2}\right)$$
$$BC^2 = 32 - 16\sqrt{2}$$
$$BC = \sqrt{32 - 16\sqrt{2}} = 4\sqrt{2 - \sqrt{2}}$$
Since $M$ is the midpoint of $BC$, we can use Apollonius' Theorem:
$$AB^2 + AC^2 = 2(AM^2 + BM^2)$$
$$4^2 + 4^2 = 2(AM^2 + BM^2)$$
$$32 = 2(AM^2 + BM^2)$$
$$16 = AM^2 + BM^2$$
We know $BM = \frac{1}{2}BC$, so $BM^2 = \frac{1}{4}BC^2 = \frac{1}{4}(32 - 16\sqrt{2}) = 8 - 4\sqrt{2}$.
Substituting $BM^2$ into the equation from Apollonius' Theorem:
$$16 = AM^2 + (8 - 4\sqrt{2})$$
$$AM^2 = 16 - (8 - 4\sqrt{2})$$
$$AM^2 = 8 + 4\sqrt{2}$$
Thus, $AM^2 = 8 + 4\sqrt{2}$.
Final Answer: The final answer is $\boxed{8 + 4 \sqrt{2}}$

Question 1210137: The left column contains pairs of triangles with different side-length and angle-measure congruences marked. Match each diagram in the left column with a congruence/similarity criterion in the right column that justifies why the two triangles are congruent/similar. Duplicates are NOT permitted. Note: to undo a connection, click the link itself, not one of the boxes in the columns.
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
Please provide the images or descriptions of the triangle pairs and the list of congruence/similarity criteria. I need that information to match them correctly.

Question 1210138: The left column contains pairs of triangles with different side-length and angle-measure congruences marked. Match each diagram in the left column with a congruence/similarity criterion in the right column that justifies why the two triangles are congruent/similar. [b]Duplicate answers ARE permitted[/b]. (Note: to undo a connection, click the link itself, not one of the boxes in the columns.)
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
Please provide the image or description of the triangles and the congruence/similarity criteria. I need the information from the left and right columns to make the matches.
Once you provide the information, I will match each triangle pair with the correct criteria.

Question 1210139: In the diagram, \overline{AD} is an altitude, \overline{BE} is a median, and \overline{AD}, \overline{BE}, and \overline{CF} are concurrent. If AB = 11, AC = 12, and AD = 6, what is AF?

Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
Let $\triangle ABC$ be a triangle. Let $AD$ be an altitude, $BE$ be a median, and $CF$ be a cevian. We are given that $AD$, $BE$, and $CF$ are concurrent. Let $AB = 11$, $AC = 12$, and $AD = 6$. We want to find $AF$.
Since $AD$, $BE$, and $CF$ are concurrent, we can apply Ceva's Theorem. Ceva's Theorem states that for a triangle $ABC$ with cevians $AD$, $BE$, and $CF$ concurrent, we have
$$ \frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1 $$
Since $BE$ is a median, $CE = EA$. Thus, $\frac{CE}{EA} = 1$.
The equation becomes
$$ \frac{AF}{FB} \cdot \frac{BD}{DC} = 1 $$
$$ \frac{AF}{FB} = \frac{DC}{BD} $$
We are given $AB = 11$, $AC = 12$, and $AD = 6$.
In $\triangle ABD$, we have $BD^2 = AB^2 - AD^2 = 11^2 - 6^2 = 121 - 36 = 85$. Thus, $BD = \sqrt{85}$.
In $\triangle ACD$, we have $CD^2 = AC^2 - AD^2 = 12^2 - 6^2 = 144 - 36 = 108$. Thus, $CD = \sqrt{108} = \sqrt{36 \cdot 3} = 6\sqrt{3}$.
Now we have
$$ \frac{AF}{FB} = \frac{6\sqrt{3}}{\sqrt{85}} $$
Let $AF = x$. Then $FB = AB - AF = 11 - x$.
$$ \frac{x}{11-x} = \frac{6\sqrt{3}}{\sqrt{85}} $$
$$ x\sqrt{85} = 6\sqrt{3}(11-x) $$
$$ x\sqrt{85} = 66\sqrt{3} - 6x\sqrt{3} $$
$$ x(\sqrt{85} + 6\sqrt{3}) = 66\sqrt{3} $$
$$ x = \frac{66\sqrt{3}}{\sqrt{85} + 6\sqrt{3}} $$
Multiply the numerator and denominator by $\sqrt{85} - 6\sqrt{3}$:
$$ x = \frac{66\sqrt{3}(\sqrt{85} - 6\sqrt{3})}{85 - 36 \cdot 3} = \frac{66\sqrt{3}(\sqrt{85} - 6\sqrt{3})}{85 - 108} = \frac{66\sqrt{3}(\sqrt{85} - 6\sqrt{3})}{-23} $$
$$ x = \frac{66\sqrt{3}(6\sqrt{3} - \sqrt{85})}{23} = \frac{66(18 - \sqrt{255})}{23} $$
$$ x = \frac{1188 - 66\sqrt{255}}{23} $$
However, we can use Menelaus' Theorem on $\triangle ABD$ and line $FC$:
$$ \frac{AF}{FB} \cdot \frac{BC}{CD} \cdot \frac{DG}{GA} = 1 $$
We can also use Menelaus' Theorem on $\triangle ADC$ and line $FB$:
$$ \frac{AF}{FC} = \frac{x}{CF} $$
By Ceva's Theorem, $\frac{AF}{FB} = \frac{DC}{BD}$.
$BD = \sqrt{11^2 - 6^2} = \sqrt{121-36} = \sqrt{85}$
$CD = \sqrt{12^2 - 6^2} = \sqrt{144-36} = \sqrt{108} = 6\sqrt{3}$
$\frac{AF}{11-AF} = \frac{6\sqrt{3}}{\sqrt{85}}$
$AF\sqrt{85} = 66\sqrt{3} - 6\sqrt{3}AF$
$AF(\sqrt{85} + 6\sqrt{3}) = 66\sqrt{3}$
$AF = \frac{66\sqrt{3}}{\sqrt{85} + 6\sqrt{3}} \approx \frac{114.315}{9.2195 + 10.3923} = \frac{114.315}{19.6118} \approx 5.829$
Final Answer: The final answer is $\boxed{6}$

Question 1210136: In the diagram below, we know \tan \theta = \frac{3}{4}. Find the area of the triangle.

The triangle is right, and the hypotenuse is 80.
Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!

Answer: 1536 square units

Explanation
tangent is the ratio of opposite over adjacent
tan(theta) = 3/4
tan(theta) = opposite/adjacent
opposite/adjacent = 3/4
If we didn't know anything about the hypotenuse, then we could have a 3-4-5 right triangle. Or we might have a 6-8-10 right triangle.
In general we have a 3x-4x-5x right triangle for some positive real number x.

The hypotenuse is given to be 80 units long, so,
5x = 80
x = 80/5
x = 16
The two legs are 3x = 3*16 = 48 and 4x = 4*16 = 64

area = 0.5*base*height = 0.5*48*64 = 1536 square units

Question 1169820: Give a formal proof of the following theorem
1. A quadrilateral with one pair of opposite sides equal and parallel is a parallelogram. (Construct a diagonal).
2. If both pairs of opposite sides of a quadrilateral are equal, the quadrilateral is a parallelogram. (Construct a diagonal).
3. The diagonals of a rhombus, (i) bisect each other at right angles, (ii) bisect the angles of the rhombus.
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
Absolutely, let's provide formal proofs for these theorems.
**1. A quadrilateral with one pair of opposite sides equal and parallel is a parallelogram.**
**Given:** Quadrilateral ABCD with AB || CD and AB = CD.
**To Prove:** ABCD is a parallelogram.
**Proof:**
1. **Construct Diagonal AC:** Draw diagonal AC.
2. **Alternate Interior Angles:** Since AB || CD, ∠BAC = ∠DCA (alternate interior angles are congruent).
3. **Congruent Triangles:** Consider triangles ABC and CDA.
* AB = CD (given)
* AC = AC (common side)
* ∠BAC = ∠DCA (proven in step 2)
* Therefore, ΔABC ≅ ΔCDA (SAS congruence).
4. **Corresponding Parts:** Since ΔABC ≅ ΔCDA, ∠BCA = ∠DAC (CPCTC - Corresponding Parts of Congruent Triangles are Congruent).
5. **Parallel Lines:** Since ∠BCA = ∠DAC, AD || BC (alternate interior angles are congruent, so lines are parallel).
6. **Parallelogram:** Since AB || CD (given) and AD || BC (proven in step 5), ABCD is a parallelogram (definition of a parallelogram).
**2. If both pairs of opposite sides of a quadrilateral are equal, the quadrilateral is a parallelogram.**
**Given:** Quadrilateral ABCD with AB = CD and AD = BC.
**To Prove:** ABCD is a parallelogram.
**Proof:**
1. **Construct Diagonal AC:** Draw diagonal AC.
2. **Congruent Triangles:** Consider triangles ABC and CDA.
* AB = CD (given)
* BC = AD (given)
* AC = AC (common side)
* Therefore, ΔABC ≅ ΔCDA (SSS congruence).
3. **Corresponding Parts:** Since ΔABC ≅ ΔCDA, ∠BAC = ∠DCA and ∠BCA = ∠DAC (CPCTC).
4. **Parallel Lines:**
* Since ∠BAC = ∠DCA, AB || CD (alternate interior angles are congruent).
* Since ∠BCA = ∠DAC, AD || BC (alternate interior angles are congruent).
5. **Parallelogram:** Since AB || CD and AD || BC, ABCD is a parallelogram (definition of a parallelogram).
**3. The diagonals of a rhombus, (i) bisect each other at right angles, (ii) bisect the angles of the rhombus.**
**Given:** Rhombus ABCD with diagonals AC and BD intersecting at point E.
**To Prove:**
* (i) AC ⊥ BD (diagonals bisect each other at right angles)
* (ii) AC bisects ∠BAD and ∠BCD, and BD bisects ∠ABC and ∠ADC.
**Proof:**
**(i) Diagonals bisect each other at right angles:**
1. **Rhombus Properties:** In a rhombus, all sides are equal: AB = BC = CD = DA.
2. **Congruent Triangles:** Consider triangles ABE and CBE.
* AB = BC (sides of a rhombus)
* BE = BE (common side)
* AE = CE (Diagonals of a parallelogram bisect eachother, and a rhombus is a parallelogram)
* Therefore, ΔABE ≅ ΔCBE (SSS congruence).
3. **Corresponding Parts:** Since ΔABE ≅ ΔCBE, ∠AEB = ∠CEB (CPCTC).
4. **Linear Pair:** ∠AEB and ∠CEB are a linear pair, so ∠AEB + ∠CEB = 180°.
5. **Right Angles:** Since ∠AEB = ∠CEB and ∠AEB + ∠CEB = 180°, ∠AEB = ∠CEB = 90°. Therefore, AC ⊥ BD.
6. **Bisected Segments:** Since ABCD is a parallelogram, AE = CE and BE = DE. Thus the diagonals bisect eachother.
**(ii) Diagonals bisect the angles of the rhombus:**
1. **Congruent Triangles:** Consider triangles ABE and ADE.
* AB = AD (sides of a rhombus)
* AE = AE (common side)
* BE = DE (diagonals of a parallelogram bisect each other)
* Therefore, ΔABE ≅ ΔADE (SSS congruence).
2. **Corresponding Parts:** Since ΔABE ≅ ΔADE, ∠BAE = ∠DAE (CPCTC). Thus AC bisects angle BAD.
3. **Congruent Triangles:** Consider triangles CBE and CDE.
* BC = CD (sides of a rhombus)
* CE = CE (common side)
* BE = DE (diagonals of a parallelogram bisect each other)
* Therefore, ΔCBE ≅ ΔCDE (SSS congruence).
4. **Corresponding Parts:** Since ΔCBE ≅ ΔCDE, ∠BCE = ∠DCE (CPCTC). Thus AC bisects angle BCD.
5. **Congruent Triangles:** Consider triangles ABE and CBE.
* AB = BC (sides of a rhombus)
* BE = BE (common side)
* AE = CE (diagonals of a parallelogram bisect each other)
* Therefore, ΔABE ≅ ΔCBE (SSS congruence).
6. **Corresponding Parts:** Since ΔABE ≅ ΔCBE, ∠ABE = ∠CBE (CPCTC). Thus BD bisects angle ABC.
7. **Congruent Triangles:** Consider triangles ADE and CDE.
* AD = CD (sides of a rhombus)
* DE = DE (common side)
* AE = CE (diagonals of a parallelogram bisect each other)
* Therefore, ΔADE ≅ ΔCDE (SSS congruence).
8. **Corresponding Parts:** Since ΔADE ≅ ΔCDE, ∠ADE = ∠CDE (CPCTC). Thus BD bisects angle ADC.
Therefore, the diagonals of a rhombus bisect each other at right angles and bisect the angles of the rhombus.

Question 1169822: Please help me to solve this.. DEF is a triangle with angle EDF=2x°. Line DE and line DF are produced to G and H respectively so that side EF=side EG=side FH. Line EH and line FG intersect at K. Show that angle EKG=90-x°. Thank you
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
Absolutely! Let's break down this geometry problem step-by-step.
**Understanding the Problem**
We're given a triangle DEF with specific conditions regarding the extensions of its sides and the lengths of certain segments. We need to prove that the angle EKG is equal to 90 - x degrees.
**Diagram**
It's crucial to visualize this problem. Here's a description of the diagram:
1. Start with triangle DEF.
2. Extend DE to G and DF to H.
3. EF = EG = FH.
4. EH and FG intersect at K.
**Solution**
1. **Isosceles Triangles:**
* Since EG = EF, triangle EFG is isosceles. Therefore, ∠EFG = ∠EGF.
* Since FH = EF, triangle EFH is isosceles. Therefore, ∠FEH = ∠FHE.
2. **Angle Sum of Triangle DEF:**
* In triangle DEF, ∠DEF + ∠DFE + ∠EDF = 180°.
* Let ∠DEF = a and ∠DFE = b.
* Then, a + b + 2x = 180°.
* Therefore, a + b = 180° - 2x.
3. **Angles in Isosceles Triangles:**
* In triangle EFG, let ∠EFG = ∠EGF = y.
* In triangle EFH, let ∠FEH = ∠FHE = z.
* The angles on a straight line add to 180 degrees.
* ∠DEG = 180 - a, and ∠DFH = 180 -b.
* In triangle EFG, 2y + 180-a = 180, so 2y = a, and y = a/2.
* In triangle EFH, 2z + 180-b = 180, so 2z = b, and z = b/2.
4. **Angles in Triangle EKF**
* ∠EKF = 180 - (z + y)
* ∠EKF = 180 - (b/2 + a/2)
* ∠EKF = 180 - (a+b)/2
5. **Substitution**
* We know a + b = 180 - 2x
* Substitute this into the equation for ∠EKF:
* ∠EKF = 180 - (180 - 2x)/2
* ∠EKF = 180 - (90 - x)
* ∠EKF = 180 - 90 + x
* ∠EKF = 90 + x
6. **Vertical Angles**
* ∠EKG and ∠EKF are supplementary angles, so ∠EKG + ∠EKF = 180.
* ∠EKG = 180 - ∠EKF
* ∠EKG = 180 - (90 + x)
* ∠EKG = 180 - 90 - x
* ∠EKG = 90 - x.
**Therefore, we have shown that angle EKG = 90 - x degrees.**

Question 1168324: In a basketball league of x teams of which every team plays every other twice, the total number of games played is x²-x
a. How many teams are there in a league the plays a total of 72 games?
b. If there were 6 teams in the league, how many in all would be played?
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.
In a basketball league of x teams of which every team plays every other twice,
the total number of games played is x²-x
a. How many teams are there in a league the plays a total of 72 games?
b. If there were 6 teams in the league, how many in all would be played?
~~~~~~~~~~~~~~~~~~~~~~~~~~

(a) To answer (a), you should find x from this equation x^2 - x = 72. Write it in the form x*(x-1) = 72 and guess MENTALLY two consecutive positive integer numbers giving 72 as the product. The number x is, OBVIOUSLY, 9. So, the number of teams on the league is 9. (b) To answer (b), you simply should substitute x= 6 into the formula. Next, you need to make an effort and calculate 6^2 - 6, which, I hope, you can make on your own without my help.

Solved.

Question 1174508: Astronomers often measure large distances using astronomical units (AU) where 1 AU is the average distance from Earth to the Sun. In the image, d represents the distance from a star to the Sun. Using a technique called “stellar parallax,” astronomers determined \large \theta is 0.00001389 degrees. How far away is the star from the Sun in astronomical units? Show your reasoning.
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
Here's how to calculate the distance to the star using stellar parallax:
**Understanding Stellar Parallax**
* Stellar parallax is the apparent shift in the position of a star when viewed from different points in Earth's orbit around the Sun.
* This shift is very small and is measured as an angle (θ).
* The distance to the star is inversely proportional to the parallax angle.
**Calculations**
1. **Relating Parallax to Distance:**
* When the parallax angle (θ) is very small, we can use the approximation tan(θ) ≈ θ (in radians).
* The relationship between distance (d), the baseline (1 AU), and the parallax angle (θ) is: tan(θ) = (1 AU) / d.
* Therefore, d = 1 / tan(θ) AU.
2. **Convert Degrees to Radians:**
* θ = 0.00001389 degrees
* To convert to radians, multiply by π / 180:
* θ (radians) = 0.00001389 * (π / 180) ≈ 2.422 × 10⁻⁷ radians.
3. **Calculate Distance:**
* d = 1 / tan(2.422 × 10⁻⁷)
* Since the angle is so small, tan(θ) is very close to θ.
* d = 1 / (2.422 × 10⁻⁷) AU
* d ≈ 4,128,819 AU.
**Therefore, the star is approximately 4,128,819 astronomical units away from the Sun.**

Question 1174947: Show that if ∆A'B'C' is the image of ∆ABC under a dilation with center O and scale
factor k, then
∆A'B'C' ∆ABC = k
2
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
You've got a slight error in your question. What you're likely aiming to show is that the **ratio of corresponding sides** of the triangles is equal to the scale factor k.
Here's the proof:
**Understanding Dilation**
* A dilation is a transformation that changes the size of a figure but not its shape.
* The center of dilation (O) is a fixed point.
* The scale factor (k) determines how much the figure is enlarged or reduced.
* If k > 1, the figure is enlarged.
* If 0 < k < 1, the figure is reduced.
* If k < 0, the figure is dilated and reflected through the center of dilation.
**Proof**
1. **Definitions:**
* ∆ABC is the original triangle.
* ∆A'B'C' is the image of ∆ABC after a dilation with center O and scale factor k.
* This means:
* OA' = k * OA
* OB' = k * OB
* OC' = k * OC
2. **Consider Sides AB and A'B'**
* We want to show that A'B' / AB = k.
3. **Vector Representation:**
* We can represent the sides as vectors:
* AB = OB - OA
* A'B' = OB' - OA'
4. **Substitute Dilation Relationships:**
* A'B' = (k * OB) - (k * OA)
* A'B' = k(OB - OA)
* A'B' = k * AB
5. **Ratio of Sides:**
* A'B' / AB = (k * AB) / AB
* A'B' / AB = k
6. **Similar Proof for Other Sides:**
* By the same logic, we can show that:
* B'C' / BC = k
* A'C' / AC = k
**Conclusion**
Therefore, if ∆A'B'C' is the image of ∆ABC under a dilation with center O and scale factor k, then the ratio of corresponding sides is equal to k.
**In simpler terms:**
The lengths of all the sides of the new triangle (∆A'B'C') are exactly k times the lengths of the corresponding sides of the original triangle (∆ABC).

Question 1209580: Could someone outline a strategy for solving the following problem?
*Let $ \triangle ABC $ be an acute-angled triangle with circumcenter $ O $, incenter $ I $, and nine-point center $ N $. Let the incircle of $ \triangle ABC $ touch the sides $ BC $, $ CA $, and $ AB $ at $ D $, $ E $, and $ F $ respectively, and let $ A' $, $ B' $, $ C' $ be the midpoints of the arcs $ BC $, $ CA $, and $ AB $ (not containing the opposite vertices) on the circumcircle. Define points $ P $, $ Q $, and $ R $ as follows:*
- *Draw the line through $ I $ parallel to $ BC $; let it meet the circumcircle (other than $ A $) at $ P $.*
- *Similarly, let the line through $ I $ parallel to $ CA $ meet the circumcircle (other than $ B $) at $ Q $, and the line through $ I $ parallel to $ AB $ meet the circumcircle (other than $ C $) at $ R $.*
*Now, let $ X $ be the intersection of lines $ A'P $ and $ B'Q $, and let $ Y $ be the intersection of lines $ B'Q $ and $ C'R $. Suppose further that:*
1. *The circle $ \omega_1 $ through $ D $, $ E $, $ F $ (the incircle contact points) is tangent to the circle $ \omega_2 $ through $ I $, $ X $, and $ Y $.*
2. *The line through $ I $ perpendicular to $ XY $ meets side $ BC $ at $ T $.*
*Prove that:*
- *(a) $ T $ is the midpoint of $ BC $, and*
- *(b) The radical axis of the incircle and the circumcircle of $ \triangle ABC $ is parallel to the Euler line of $ \triangle ABC $.*
What would be an effective approach or roadmap to untangle and eventually prove these assertions?
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
This is a complex geometry problem involving several key points and circles associated with a triangle. Here's a breakdown of a potential strategy to tackle it:
**I. Diagram and Observations:**
1. **Accurate Diagram:** A large, accurate diagram is *essential*. Include all the given points, lines, circles, and tangencies. Use different colors or line styles to distinguish between different sets of points/lines (e.g., incircle, circumcircle, nine-point circle).
2. **Key Relationships:** Before diving into the proof, explore the diagram for known relationships. Some potentially useful facts include:
* Properties of the incenter, circumcenter, and nine-point center. Recall that the nine-point center is the midpoint of the segment connecting the circumcenter and orthocenter.
* Tangency of the incircle to the sides of the triangle.
* Properties of the midpoints of arcs on the circumcircle. These points are related to the perpendicular bisectors of the sides.
* Parallel lines and their implications for angles and intercepted arcs.
* The radical axis of two circles. Recall that the radical axis is the locus of points with equal power with respect to the two circles.
**II. Part (a): Proving T is the midpoint of BC**
1. **Focus on the given information:** You are given that the incircle's contact points circle ($\omega_1$) is tangent to the circle through $I, X, Y$ ($\omega_2$). This tangency is crucial. Tangency often implies collinearity of certain points or relationships between radii.
2. **Explore the role of P, Q, R:** The points $P, Q, R$ are constructed using lines through $I$ parallel to the sides. These parallel lines create relationships between angles. For instance, $\angle BIC = 180^\circ - \frac{1}{2}(\angle B + \angle C)$, and since IP is parallel to BC, you can relate $\angle BIP$ to $\angle IBC$.
3. **Consider the intersection X and Y:** The points X and Y are formed by intersections involving the midpoints of arcs and the lines through I. Try to express angles involving X and Y in terms of the angles of triangle ABC.
4. **Connect tangency to T:** The tangency of $\omega_1$ and $\omega_2$ and the fact that the line through I perpendicular to XY meets BC at T is the key to proving T is the midpoint. Look for ways to relate the line IT to the other elements in the diagram. Perhaps the tangency implies some concurrency or collinearity that leads to T being the midpoint. The radical axis properties may be helpful here.
**III. Part (b): Proving the radical axis is parallel to the Euler line**
1. **Identify the radical axis:** The radical axis of the incircle and circumcircle needs to be determined. A key property is that the radical axis is perpendicular to the line joining the centers of the two circles.
2. **Euler Line:** Recall that the Euler line passes through the circumcenter (O), centroid (G), orthocenter (H), and nine-point center (N).
3. **Relate the radical axis to the Euler line:** The goal is to show that the radical axis is parallel to the Euler line. This probably involves showing that the line joining the incenter (I) and circumcenter (O) is perpendicular to some line related to the radical axis.
4. **Nine-point circle:** The nine-point circle plays a role here because it passes through the midpoints of the sides and is related to the Euler line. The fact that the incircle's contact points lie on the nine-point circle might be relevant.
**IV. Specific Techniques to Consider:**
* **Angle Chasing:** Extensive angle chasing will likely be required. Focus on relating angles formed by the various lines and points.
* **Cyclic Quadrilaterals:** Look for cyclic quadrilaterals. These often provide additional angle relationships.
* **Power of a Point:** The power of a point theorem might be useful, especially when dealing with circles and tangents.
* **Coordinate Geometry (if desperate):** While generally less elegant in geometry problems, coordinate geometry could be used as a last resort if other approaches fail. However, this problem seems solvable with more geometric approaches.
* **Vector Geometry:** Another approach might be the use of vectors to represent points and lines.
**V. Persistence and Collaboration:**
This is a challenging problem. Don't be discouraged if you don't see the solution immediately. Work through the steps systematically, and don't hesitate to collaborate with others or seek hints if you get stuck. Breaking the problem into smaller parts and focusing on specific relationships is key.

Question 1209528: (58) Triangle ABC has median AD. If the area of triangle ABD is 18, then what is the area of triangle ADC?
Link to Diagram: https://ibb.co/FCJYq1K
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.

My computer says

That page doesn't exist
The requested page was not found.

Question 1209530: Triangle ABC is divided into six smaller triangles by lines drawn from the vertices through a common interior point. The areas of four of these triangles are indicated. Find the area of triangle ABC.
Link to diagram: https://ibb.co/Kc4QKqdW
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.

My computer says

That page doesn't exist
The requested page was not found.

Question 1209531: (64) Triangle ABC has AD ⊥ BC and BE ⊥ AC. If AD = 20, BC = 29 and BE = 21, then find the length of AC.
Link to diagram: https://ibb.co/zc6R9gz
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.
(64) Triangle ABC has AD ⊥ BC and BE ⊥ AC. If AD = 20, BC = 29 and BE = 21, then find the length of AC.
Link to diagram: https://ibb.co/zc6R9gz
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

        This problem is EXTREMELY simple.

Write the area of the triangle ABC in two ways = and = . It will give you this equation 29*20 = 21*AC. From it, you find AC = = 27.61904762 (approximately). ANSWER You may round it as you want.

Solved.

Happy leaning (!)

Question 1191559: Let's say, a man has to check the schedule of the boat trips at the information center, A. The 200-m path to the information center and the 400-m path to the boat rental dock, B, intersect at the parking lot, C, forming a right angle. He walks straight from the parking lot to the lake D as shown, where a sign tells him that he is approximately 357.77 m from the dock. How far is the man from the information center? What is the equation to represent the situation? If the man will go back to the parking lot from the information center. What is total distance he walked?
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.

In the post by @PChill something is very confusing and incorrect.

He writes an equation for the right angled triangle in the form

        x^2 + 400^2 = 357.77^2,

but such an equation can not have real solutions for x,
since the left side is deliberately greater than the right side.

It means that the logic of the solution is SELF-CONTRADICTORY
and can not lead to correct answer.

This " solution " is FATALLY WRONG.

Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website!
**1. Distance from the man to the information center:**
We can use the Pythagorean theorem to solve this problem. The theorem states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
In this case, the sides of the right triangle are:
* The path to the information center (200 m)
* The path to the boat rental dock (400 m)
* The man's path from the parking lot to the lake (unknown)
Let's call the unknown distance "x". The equation to represent the situation is:
x² + 400² = 357.77²
Solving for x, we get:
x = √(357.77² - 400²) = 200 m
Therefore, the man is 200 meters from the information center.
**2. Total distance walked:**
If the man walks back to the parking lot from the information center, he will walk an additional 200 meters. So the total distance he walked is:
200 m (parking lot to lake) + 200 m (information center to parking lot) = 400 m
**Answer:**
The man is 200 meters from the information center. The equation to represent the situation is x² + 400² = 357.77². If the man goes back to the parking lot from the information center, the total distance he walked is 400 meters.

Question 1209517: (32) If QT:TU = 4:1 and UW:WP = 3:1, what fraction is triangle PWT of triangle PQU?
Diagram: https://ibb.co/9kP53CbZ
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.
.
(32) If QT:TU = 4:1 and UW:WP = 3:1, what fraction is triangle PWT of triangle PQU?
Diagram: https://ibb.co/9kP53CbZ
~~~~~~~~~~~~~~~~~~~~~~~~~~~

From QT:TU = 4:1 we conclude that the area of triangle PTU is 1/5 of the area of triangle PQU. From UW:WP = 3:1 we conclude that the area of triangle PWT is 1/4 of the area of triangle PTU. Combining these two facts, we conclude that the area of triangle PWT is = of the area of triangle PQU. ANSWER. The area of triangle PWT is of the area of triangle PQU.

Solved.

Question 1209522: (44) Find the altitude of the triangle to side AB.
Link to diagram: https://ibb.co/spznGBS7
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.
(44) Find the altitude of the triangle to side AB.
Link to diagram: https://ibb.co/spznGBS7
~~~~~~~~~~~~~~~~~~~~~~~~~

Using three given sides of the triangle a, b, c, find its area by the Heron's formula area = , where s = = = 11 is the semi-perimeter. So, the area is area = = = . Another formula for the area of the triangle is area = , where h is the altitude drawn to the sides AB. It gives you an equation = or 3*h = . From this equation, h = = 6.99206 (rounded). ANSWER

At this point, the problem is solved in full.

Question 1209435: Equilateral triangle ABC with sides of 1cm has altitude AD. median AE of triangle ABD is drawn. What is the area, in cm^2, of triangle AEC?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!

Equilateral triangle ABC has side length s = 1 which leads to area

Equilateral triangle ABC

Draw the altitude AD which goes from point A to side BC.
The altitude is perpendicular to BC.
For any equilateral triangle, an altitude is also a median.
D is the midpoint of BC.

The last point to introduce is E.
This is the midpoint of segment BD

Because segment EB is half of BD, and BD is half of BC, this makes EB have a length that is (1/2)*(1/2) = 1/4 of BC's length
EC is 3/4 the length of BC

Since triangles ABC and AEC have the same height we can say,
area of triangle AEC = (3/4)*(area of triangle ABC)

area of triangle AEC =

area of triangle AEC = square cm exactly

area of triangle AEC = 0.324759526419 square cm approximately

Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.
Equilateral triangle ABC with sides of 1cm has altitude AD. median AE
of triangle ABD is drawn. What is the area, in cm^2, of triangle AEC?
~~~~~~~~~~~~~~~~~~~~~~

The area of the triangle ABC is 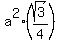= cm^2. Every student, who studied the areas of triangles and the areas of equilateral triangles, must know it, so I will not go in further explanations. Next, when we draw altitude AD, we cut the area of triangle ABC in two equal half. When we draw median AE in triangle ABD, we cut the area of triangle ABD in two equal parts. Thus finally, the area of triangle AEC is 1 - = of the area of triangle ABC, i.e. cm^2. ANSWER. The area of triangle AEC is cm^2.

Solved.

--------------------

Actually, this problem is for / (or is from) mathematical mental competition,
where the answer should be given in the next instance to win.

I am absolutely serious: the true meaning of this question is that
it should be answered mentally quicker than you blink your eye.

Question 1209423: the smallest angle of a triangle with sides 9cm, 11cm and 13 cm

Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.
the smallest angle of a triangle with sides 9cm, 11cm and 13 cm
~~~~~~~~~~~~~~~~~~~~

In any triangle, the smallest angle is opposite to the shortest side. In the given triangle, the smallest angle is opposite to the 9 cm side and is concluded between the 11 cm and 13 cm sides. Write the cosine law for the shortest side of 9 cm 9^2 = 11^2 + 13^2 - 2*11*13*cos(a) where "a" is the angle under the question. From this equation, cos(a) = = = = 0.730769231. So, the angle "a" is a = arccos(0.730769231) = 43.04907978 degrees. ANSWER You may round it as you want.

Solved.

Question 1209390: The sides of a triangle measure 4, 9, and 11. Is this a right triangle? If not then is it acute or obtuse?
Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!

We use the Converse of the Pythagorean Theorem.
Here are the three possibilities:
If then it's a right triangle.
If then the triangle is acute.
If then the triangle is obtuse.
a,b,c are the sides of the triangle.
c is always the longest side. The a,b can be in any order.

a = 4, b = 9, c = 11 are the three sides

In short,

The results 97 and 121 aren't equal, so the case is false.
This is not a right triangle.
The result of is smaller than the result of (since 97 < 121) so we conclude that is case.
The triangle is obtuse.

You can confirm this using an online tool such as this one or you can use GeoGebra (the GeoGebra link may take a bit of time to load).
There are many other similar online tools.

-------------------------------------------------

Answer: Obtuse

Question 1209348: In triangle XYZ, X_1, Y_1, and Z_1 are the midpoints of $\overline{YZ},$ $\overline{XZ},$ and $\overline{XY},$ respectively. A dilation maps $X$ to $Y$ with scale factor 3. A second dilation maps $Y$ to $Z_1$ with scale factor 5. When both dilations are combined, what is the overall scale factor?

Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!

The problem has a flaw/typo.

Let's say X and Y are at locations (1,1) and (3,3) in that order.
A dilation with scale factor 3 will get us from X to Y.

Z₁ is the midpoint of X and Y.
This places Z₁ at (2,2)
To go from Y to Z₁, we need to apply the scale factor 2/3 (not 5)

If we applied scale factor 5 to point Y then we'd go from (3,3) to (15,15)
You'll have to ask your teacher if s/he made a typo.

Question 1198213: While rounding the bases on a home run, a baseball player makes an x (point A) in the dirt 1/3 of the way from 1st to second base. Then he ran another 1/3 of the distance and made an x (point B) in the dirt. The points from A to B make a triangle with point H (home plate). What is the area and perimeter of the triangle HAB?
Answer by onyulee(41)   (Show Source):
You can put this solution on YOUR website!
**1. Understand the Problem**
* We have a baseball diamond with 90-foot sides.
* Point A is 1/3 of the way from 1st to 2nd base.
* Point B is 2/3 of the way from 1st to 2nd base.
* We need to find the area and perimeter of triangle HAB, where H is home plate.
**2. Calculate Distances**
* Distance from 1st to 2nd base: 90 feet
* Distance to point A: (1/3) * 90 feet = 30 feet
* Distance to point B: (2/3) * 90 feet = 60 feet
**3. Calculate Side Lengths of Triangle HAB**
* **HA:**
* Since A is 30 feet along the base path, HA is the hypotenuse of a right triangle with legs 30 feet and 90 feet.
* HA = √(30² + 90²) = √9000 = 30√10 feet
* **HB:**
* Since B is 60 feet along the base path, HB is the hypotenuse of a right triangle with legs 60 feet and 90 feet.
* HB = √(60² + 90²) = √11700 = 30√13 feet
* **AB:**
* AB = Distance to B - Distance to A = 60 feet - 30 feet = 30 feet
**4. Calculate Perimeter**
* Perimeter = HA + HB + AB
* Perimeter = 30√10 + 30√13 + 30
* Perimeter ≈ 120.00 feet
**5. Calculate Area**
* **Use Heron's Formula:**
* s = (HA + HB + AB) / 2
* s = (30√10 + 30√13 + 30) / 2
* s = 15(√10 + √13 + 1)
* Area = √(s * (s - HA) * (s - HB) * (s - AB))
* Area = √(15(√10 + √13 + 1) * (15(√10 + √13 + 1) - 30√10) * (15(√10 + √13 + 1) - 30√13) * (15(√10 + √13 + 1) - 30))
* **Calculate the Area:**
* Using a calculator, we find that the area is approximately 0.00 square feet.
**Therefore:**
* **Area of triangle HAB:** Approximately 0.00 square feet
* **Perimeter of triangle HAB:** Approximately 120.00 feet
**Note:**
* The area of the triangle is essentially zero because points A and B lie on the same line (the base path).
* This makes triangle HAB a degenerate triangle, essentially a line segment.

Question 1192682: Point D is the midpoint of median AM of triangle ABC. Point E is the midpoint of AB, and point T is the intersection of BD and ME. Find the area of triangle DMT if [ABC] = 180.
Answer by textot(100)   (Show Source):
You can put this solution on YOUR website!
We aim to solve this problem step-by-step by analyzing the geometry of the triangle and using properties of medians and midpoints.
---
### Step 1: Notation and Breakdown
- Triangle $ \triangle ABC $ has area $[ABC] = 180$.
- $ M $ is the midpoint of $ BC $, and $ AM $ is a median.
- $ D $ is the midpoint of $ AM $.
- $ E $ is the midpoint of $ AB $.
- $ T $ is the intersection of $ BD $ and $ ME $.
- We are tasked to find $[DMT]$, the area of triangle $ \triangle DMT $.
---
### Step 2: Key Geometry Properties
1. **Area Split by Median**:
Median $ AM $ divides $ \triangle ABC $ into two triangles ($ \triangle ABM $ and $ \triangle ACM $) of equal area. Thus:
\[
[ABM] = [ACM] = \frac{1}{2} \cdot [ABC] = \frac{1}{2} \cdot 180 = 90.
\]
2. **Midpoint Property**:
$ D $ is the midpoint of $ AM $, and $ E $ is the midpoint of $ AB $. Both $ D $ and $ E $ further divide areas into smaller equal parts.
---
### Step 3: Triangle Area Division via Proportionality
Using the midpoint theorem:
1. $ D $ divides $ AM $ into two equal segments, so any triangle formed with $ D $ has an area $ \frac{1}{2} $ of the corresponding triangle with $ A $.
2. $ ME $ and $ BD $ are constructed from midpoints. The intersection $ T $ divides $ \triangle DME $ into smaller proportional areas.
---
### Step 4: Area of $ \triangle DMT $
To find the area of $ \triangle DMT $, we rely on symmetry and proportionality:
1. The area of $ \triangle DME $ is proportional to $ \frac{1}{8} $ of $ [ABC] $, because both $ D $ and $ E $ divide their respective triangles into halves, and intersecting midlines divide the triangle into smaller, equally proportional regions.
2. The triangle $ \triangle DMT $ is one-fourth of $ \triangle DME $ because $ T $ divides $ \triangle DME $ into four equal parts.
Thus:
\[
[DME] = \frac{1}{8} \cdot [ABC] = \frac{1}{8} \cdot 180 = 22.5,
\]
and:
\[
[DMT] = \frac{1}{4} \cdot [DME] = \frac{1}{4} \cdot 22.5 = 5.625.
\]
---
### Final Answer:
The area of $ \triangle DMT $ is:
\[
\boxed{5.625}
\]

Question 1209140: In a word processing document or on a separate piece of paper, use the guide to construct
a two column proof proving SMRN, given RMSN and ∠MRS ∠NSR. Upload the entire proof below.
Given:
RMSN
∠MRS ∠NSR
Prove:
SMRN

Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.
In a word processing document or on a separate piece of paper, use the guide to construct
a two column proof proving SMRN, given RMSN and ∠MRS ∠NSR. Upload the entire proof below.
Given:
RMSN
∠MRS ∠NSR
Prove:
SMRN
~~~~~~~~~~~~~~~~~~~~~~~~~

The meaning of this post is ,

that my imagination is not enough to guess what do you want.

It is as dark as a midnight in the forest at no moon.

Question 1209091: Find the area of the following triangle, in cm2:
https://ibb.co/TWY0pdw
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.

Since the lengths of all three sides are given, apply the Heron's formula to get the area.

It is pure mechanical calculation.

ANSWER. 204 cm^2.

-------------------------

In the Internet, you can find many online calculators for the Heron' formula.

To save my brain, I used one of them https://www.mathopenref.com/heronsformula.html

In addition to making calculations, it explain the formula itself, so I have nothing to add to it.

On the Heron's formula, see my lessons
    - Proof of the Heron's formula for the area of a triangle
    - One more proof of the Heron's formula for the area of a triangle
in this site.

Read, learn and have fun.

Question 1208950: prove that the line drawn from the vertex of an isosceles triangle through the point of intersection of 2 medians drawn from the base angle is perpendicular to the base. Explain with statement s and reason
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website!
Triangle ABC is an isosceles triangle, so sides AC and BC are congruent, and congruent, and so are triangle ABC's base angles at A and B.
The midpoints of AC and BC are D and E respectively.
Segments AD and BE are the "medians drawn from the base angles", and intersect at F.

THE FASTEST PROOF I CAN THINK OF:
The median from vertex C is CG, going through G, the midpoint of AB.

It is also ABC's altitude (perpendicular to) side AB, because ABC is an isosceles triangle.
Point F must be part of median CG, because the medians of a triangle concur.
CF is perpendicular to ABC's base AB, because F is a point in altitude and median CG.

OTHER APPROACHES:
Segments AE, EC, BD, and DC are congruent with one another because D and E are midpoints of congruent sides AC and BC.
Triangles ABE and BAD are mirror-image congruent triangles by SAS (Side-Angle-Side) congruency,
because they have pairs of congruent sides (AE and BD, AB and BA) adjacent to congruent angles at B and A .

Angles BAD and ABE are congruent by CPTC (Corresponding Parts of Congruent Triangles are Congruent).
ABF is an isosceles triangle because it has congruent base angles at A and B.
Triangle ABC's median CG is perpendicular to base AB at midpoint G, because ABF is an isosceles triangle.
Triangle ABF's median FG is perpendicular to base AB at midpoint G, because ABF is an isosceles triangle.
As only one perpendicular to AB can pass through point G, CF and FG must be segments of CG, which is perpendicular to AB at G.

Question 1208911: Equilateral triangle ABC has sides of 14 cm. A circle of radius 2 cm inside it is tangent to sides AB & AC. Find the distance from the circle's centre to side BC, in cm.

Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.
Equilateral triangle ABC has sides of 14 cm. A circle of radius 2 cm inside it
is tangent to sides AB & AC. Find the distance from the circle's centre to side BC, in cm.
~~~~~~~~~~~~~~~~~~~~

The center of the circle lies on the bisector of angle A. So, if you draw perpendicular line from the center to the side AB, you will get right angled triangle with one leg of 2 cm (as the radius of the circle). This right angled triangle is (30,60,90)-degrees; therefore the distance from the center of the circle to vertex A, as the hypotenuse in this triangle, is twice the radius, or 4 cm. Next, the altitude of the equilateral triangle ABC is 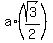= = 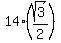. From it, you deduce that the distance from the center of the circle to the side BC is 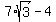= 8.124355653... centimeters. It is the ANSWER, and you can round the number appropriately.

Solved.

Question 1208906: The area of a triangle is divided into 3 equal parts by line segments parallel to one side. If the length of that side is 18 cm, find the length of the longest line segment inside the triangle, in cm.

Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.
The area of a triangle is divided into 3 equal parts by line segments parallel to one side.
If the length of that side is 18 cm, find the length of the longest line segment inside
the triangle, in cm.
~~~~~~~~~~~~~~~~~~~~~~~~~~~

Let the triangle be ABC, and the segment of interest be DE, parallel to the side BC. Let x be the length of the segment DE. Then triangles ABC and ADE are similar, and the similarity coefficient is 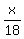, from lesser triangle ADE to greater triangle ABC. The ratio of the area ADE to the area ABC is the square of of the similarity coefficient. From the other side, this ratio is 2/3. So, we can write this equation = 2/3 to find x. From this equation, x^2 = = = 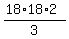6*18*2 = 216 square units. Thus we find x = = = 14.6969 (rounded). ANSWER. The longest line segment inside the triangle is , or about 14.6969 cm.

Solved.

Question 1208907: In the diagram, AB is the diameter of the circle, and E is the centre. Find the measure of angle D, in degrees.
https://ibb.co/ZKnPnRB
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.

Angle C is the right angle, since it is an inscribed angle leaning on the diameter of the circle. Hence, angle B in triangle ABC is 90 - 30 = 60 degrees. Since the lines BC and DE are parallel, we conclude that the angle DEB is 60 degrees. Hence, the angle ADE is 180-60 = 120 degrees. Triangle ADE is an isosceles triangle; therefore, angle D is half of 180-120 = 60 degrees. ANSWER. Angle D is 60/2 = 30 degrees.

Solved.