Question 804120: A swimmer can swim a distance of 36 kilometer in the direction of water current in the same time, which he requires to swim 36 kilometers in the opposite direction of water current in stream. If in still water, swimmer has speed of 12 kilometer/ hour more than the speed of that of water in stream, the what is the speed of water?
A. 3Km/hr
B. 9 Km/hr
C. 12 Km/hr
D. 18 Km/hr
help me plz to solve this question....
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Something is very wrong with this problem.
Maybe something got lost in translation.
To begin, no human swimmer can swim at 12 km/hour in still water. Not even for a short distance. Not even an Olympic champion. The swimmer in the problem must not be a human.
Something is very wrong with this problem, even if the swimmer is much faster than any human.
If there is a current, in the same time, the swimmer will go much farther in the direction of water current than when swimming in the opposite direction.
If the swimmer can go 36 kilometers in the same time, with or against the current, then the current goes so slow that the swimmer does not notice the current.
If in still water the swimmer has a speed of 12 kilometer/ hour more than the speed of that of water in stream, and the speed of the stream is  kilometer/ hour, the speed of the swimmer with respect to the ground on the edges of the stream will be kilometer/ hour, the speed of the swimmer with respect to the ground on the edges of the stream will be
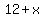 kilometer/ hour in still water the swimmer, kilometer/ hour in still water the swimmer,
 kilometer/ hour in the direction of water current, and kilometer/ hour in the direction of water current, and
 kilometer/ hour in the opposite direction of water current in stream. kilometer/ hour in the opposite direction of water current in stream.
With the same speed of the stream, it will take the swimmer a longer time to cover the same 36 kilometers when swimming against the current. How much longer depends on the current.
It will take the swimmer
 hours to swim a distance of 36 kilometer in the opposite direction of water current in stream. hours to swim a distance of 36 kilometer in the opposite direction of water current in stream.
It will take the swimmer a shorter time,
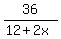 hours, to swim a distance of 36 kilometer in the direction of water current. hours, to swim a distance of 36 kilometer in the direction of water current.
If it takes the swimmer  hours longer to cover the same 36 kilometers when swimming against the current, hours longer to cover the same 36 kilometers when swimming against the current,

If we know  we can calculate we can calculate  as as 
If we know  we can calculate we can calculate  as as 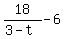 . .
If the stream speed is  , then the downstream swim takes 2 hours and , then the downstream swim takes 2 hours and  is the difference. is the difference.
For  , ,  and the swim downstream takes only 1.2 hours. and the swim downstream takes only 1.2 hours.
For  , ,  and the swim downstream takes only 1 hour. and the swim downstream takes only 1 hour.
For  , ,  and the swim downstream takes only 0.75 hours (45 minutes). and the swim downstream takes only 0.75 hours (45 minutes).
|
|
|