Question 803720: A boats start To cross a river upstream at an angle of 140 deg to the flaw of the river the boat moves directly across the river at 10m/s as a result of combined effect of the velocity of the stream and the velocity of the boat. Calculate
(a) the velocity of the stream.
(b)the velocity of the boat in still in water.
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! You may be able to draw this picture:
Horizontal axis, current of river toward the right; vertical axis, upward is "accross" the river straight up.
The boat is trying to go into quadrant 4, so that direction of the boat vector is 140 degrees, using "to the right..." as the reference direction, the positive x axis. The river vector is just toward the right, no angle, since angle 0 is unrotated and toward the right.
b for the boat's magnitude, r for the river's magnitude.
The boat vector is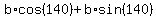 
The river vector is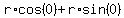 
The sum of the vectors for b and r is 
Adding the components will give you two equations.
 and 
 and 
 and 
'
 and 
Second part simplified is then  , and therefore  .
If you prefer for proper accuracy,  and  .
|
|
|
