SOLUTION: PLEASE SOLVE THIS QUESTION FROM LINEAR EQUATIO IN TWO VARIABLES ITS TROUBLING ME A LOT Q:A cyclist after travelling a certain distance stopped for 30 minutes to repair the cycle.T

Algebra ->  Customizable Word Problem Solvers  -> Travel -> SOLUTION: PLEASE SOLVE THIS QUESTION FROM LINEAR EQUATIO IN TWO VARIABLES ITS TROUBLING ME A LOT Q:A cyclist after travelling a certain distance stopped for 30 minutes to repair the cycle.T      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 4488: PLEASE SOLVE THIS QUESTION FROM LINEAR EQUATIO IN TWO VARIABLES ITS TROUBLING ME A LOT
Q:A cyclist after travelling a certain distance stopped for 30 minutes to repair the cycle.Then he completed the whole journey of 30km at half the speed and took a total time of 5hours.If the breakdown has occured 10km further off,he would have completed the whole journey in 4hours.Find where the breakdown occoured and his original speed.
ANSWER:15 KM FROM THE STARTING POINT:SPEED:10KM/HR(GIVEN IN THE BOOK)
Answer by longjonsilver(2297) About Me  (Show Source):
You can put this solution on YOUR website!
OK, I would first draw a distance-time graph for each journey, to help visualise the question. I cannot show this easily here though, so i shall just have to define some things:
First journey:
Let d = distance travelled before the break
Let t%5B1%5D = time taken to travel this distance
Let v = speed of this part of the journey
Let 30-d = distance travelled after the break
Let 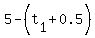5-%28t%5B1%5D%2B0.5%29 be the time taken to travel this second part
Let v/2 = speed of this final part of the journey

Second Journey
Let d+10 = distance travelled before the break
Let t%5B2%5D = time taken to travel this distance
Let v = speed of this part of the journey
Let 30-(d+10) = distance travelled after the break
Let 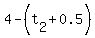4-%28t%5B2%5D%2B0.5%29 be the time taken to travel this second part
Let v/2 = speed of this final part of the journey

You need to understand these definitions in the context of the question. If you do not, you will just see it as "magic" on my part and you will not learn from it.

The question wants v and d, so we will be looking to remove the 2 times, t%5B1%5D and t%5B2%5D.

Basically, all I shall use now is the definition of speed=distance/time. So, for the 2 parts of the first journey we get:

v=d%2Ft%5B1%5D --eqn1 and %28v%2F2%29+=+%28%2830-d%29%2F%285-%28t%5B1%5D%2B0.5%29%29%29 -- eqn2

Eqn1 can be re-written as t%5B1%5D=d%2Fv

Now, eqn2 is worked on as follows (remember we want t%5B1%5D= so we can equate both versions together). So...

v+=+%282%2830-d%29%2F%284.5-%28t%5B1%5D%29%29%29
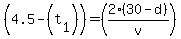
%284.5-%28t%5B1%5D%29%29+=+%282%2830-d%29%2Fv%29
%28t%5B1%5D%29+=+4.5+-+%282%2830-d%29%2Fv%29

So, we now know 2 different equations that both equal
%28d%2Fv%29+=+4.5+-+%2860-2d%29%2Fv
%28d%2Fv%29+=+4.5+-+60%2Fv+%2B+2d%2Fv
-d%2Fv+=+4.5+-+60%2Fv
-d%2Fv+%2B+60%2Fv+=+4.5 --eqn3

Now we do the same for the second journey:

v+=+%28d%2B10%29%2F%28t%5B2%5D%29 and %28v%2F2%29+=+%2830-%28d%2B10%29%29%2F%284-%28t%5B2%5D%2B0.5%29%29

Re-arrange both of these to get t2= then equate these and simplify to give (60/v) - (d/v) = 3.5 + (10/v) --eqn4

Now, you can see eqn3 and eqn4 have the same lefthand side, so this means that their righthand sides are the same, ie 4.5 = 3.5 + 10/v

so, 1 = 10/v --> v=10

Now, put this value back into eqn3 or eqn4 to find d.

Hope this all makes sense.

jon.
PS there is an error on this page - i cannot seem to fix it. Email Igor to ask him to fix it, then the page will view correctly.