SOLUTION: There are two cities, A, and B. A fast train can go from A to B in 8 hours. A slow train can go from B to A in 12 hours. They start from the two cities toward each other at the sam

Algebra ->  Customizable Word Problem Solvers  -> Travel -> SOLUTION: There are two cities, A, and B. A fast train can go from A to B in 8 hours. A slow train can go from B to A in 12 hours. They start from the two cities toward each other at the sam      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1163985: There are two cities, A, and B. A fast train can go from A to B in 8 hours. A slow train can go from B to A in 12 hours. They start from the two cities toward each other at the same time. when they met, the fast train went 192 km more than the slow train. How far is it from A and B?
Found 3 solutions by ankor@dixie-net.com, ikleyn, greenestamps:
Answer by ankor@dixie-net.com(22740) About Me  (Show Source):
You can put this solution on YOUR website!
There are two cities, A, and B. A fast train can go from A to B in 8 hours.
A slow train can go from B to A in 12 hours.
They start from the two cities toward each other at the same time.
when they met, the fast train went 192 km more than the slow train.
How far is it from A and B?
:
let x = the distance traveled by the slow train to the meeting point
then
(x+192) = the distance traveled by the fast train to the meeting point
and
(2x+192) = the distance from A to B
:
An inverse relationship between the distance and the travel times from A to B
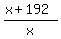%28x%2B192%29%2Fx%29 = 12%2F8
12x = 8(x+192)
12x = 8x + 1536
12x - 8x = 1536
4x = 1536
x = 1536/4
x = 1536/4
x = 384 km from B to the meeting point
then
192+384 = 576 km from A to the meeting point
and
384 + 576 = 960 km from A to B
:
:
:
Check; find the actual speed of each
960/8 = 120 km/hr, the fast train
960/12 = 80 km/hr, the slow
:
Find the times to the meeting point, should be equal
576/120 = 4.8 hrs
384/80 = 4.8 hrs

Answer by ikleyn(52786) About Me  (Show Source):
You can put this solution on YOUR website!
.

Let d be the distance between the cities, in kilometres.


Then the rate of train A is  d%2F8  km/h;  the rate of the train B is  d%2F12 km/h.


The time from the start to the meeting point is the same, so the traveled distances  d%5BA%5D  and  d%5BB%5D
by the trains are in the same ratio as their rates


    d%5BA%5D%2Fd%5BB%5D = %28%28d%2F8%29%29%2F%28%28d%2F12%29%29 = 12%2F8 = 3%2F2.


It implies  that the distance traveled by train A before they met was  d%2A%283%2F%283%2B2%29%29 = %283%2F5%29d;

                 the distance traveled by train B before they met was  d%2A%282%2F%283%2B2%29%29 = %282%2F5%29d.


We are given that

    %283%2F5%29d - %282%2F5%29d = 192.


It means that

    %281%2F5%29d = 192;


hence,  d = 5*192 = 960 kilometers.


ANSWER.  The distance between the cities is 960 kilometers.

Solved.



Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


The ratio of the times required for the two trains to make the whole trip is 8:12 = 2:3.

That means the ratio of the speeds of the two trains is 3:2.

Since the ratio of the speeds is 3:2, and since the times traveled (to the point where the trains meet) are the same, the distances the two trains travel are in the ratio 3:2.

So let the distances traveled by the two trains be 3x and 2x.

The difference between the two distances is then x; and we are told that difference is 192 km. So x = 192.

The total distance between the two cities is the sum of the distances the two trains traveled, which is 3x+2x=5x = 5(192) = 960 km.

ANSWER: The distance between the cities is 960 km.