Question 1163672: Driving between City A and City B, the ratio of the time Sam takes to the time Richard takes is 5 : 4. If Sam leaves City A and Richard leaves City B at the same time toward to each other, they meet in 40 minutes, and they continue to drive. After Richard arrives at City A, how many minutes later will Sam arrives at City B?
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52782)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let  be the time Sam takes to drive from A to B, and
Let be the time Sam takes to drive from A to B, and
Let  be the time Richard takes to drive from B to A.
We are given be the time Richard takes to drive from B to A.
We are given
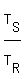 = =  , or , or  = = 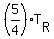 (1)
Hence, the ratio of their rates per minute is reciprocal ratio (1)
Hence, the ratio of their rates per minute is reciprocal ratio
 = =  , or , or  = =  = =  . (2)
The total distance equation is . (2)
The total distance equation is
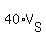 + +  = d (3)
Replace here = d (3)
Replace here  = =  based on (2). You will get based on (2). You will get
 + +  = d, or = d, or
 + +  = d = d
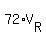 = d
which implies that the time = d
which implies that the time 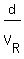 = 72 minutes.
Thus, Richard completes his trip in 72 minutes: = 72 minutes.
Thus, Richard completes his trip in 72 minutes:  = 72 minutes.
Then the time by Sam is = 72 minutes.
Then the time by Sam is  = see (1) = = see (1) = 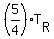 = =  = 90 minutes.
Thus Sam reaches B 90-72 = 18 minutes after Richard reaches A. ANSWER = 90 minutes.
Thus Sam reaches B 90-72 = 18 minutes after Richard reaches A. ANSWER
Solved.
---------------
Surely, this problem is two levels higher than a regular Math/Physics problem in any high school.
It is, actually, an Olympiad level problem in Physics.
Could you tell me please where is it from, from which source ?
Do not forget to post your "THANKS" to me for my teaching.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Driving between City A and City B, the ratio of the time Sam takes to the time Richard takes is 5 : 4. If Sam leaves City A and Richard leaves City B at the same time toward to each other, they meet in 40 minutes, and they continue to drive. After Richard arrives at City A, how many minutes later will Sam arrives at City B?
Let multiplicative factor be x, and distance from A to B, or B to A, D
Then times Sam and Richard take to complete journey are 5x and 4x, respectively
Therefore, Sam’s speed = 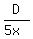 , and Richard’s is: , and Richard’s is: 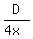
With them meeting in 40 minutes, we get: 
 ------- Factoring out GCF, D, in numerators ------- Factoring out GCF, D, in numerators
4 + 5 = 30x ------ Mulltiplying by LCD, 30x
9 = 30x
Multiplicative factor, or 
Therefore, the difference in times for them to complete their respectively journeys is 
|
|
|