Question 1150458: On a day when visibility was limited to 1700m, a ship of the Blue Line was traveling west, on a parallel course to a ship of the White Line travelling east, with the courses 800m apart. The Blue Line ship’s velocity was 8 km/h. If the ships were in sight of each other for 15 minutes, what was the velocity, in km/h, of the White Line ship?
Answer by ikleyn(52800)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The configuration, when they see each other for the first time, is the right angled triangle with one leg of 800 meters
and the hypotenuse of 1700 meters.
Then the other leg is  = 1500 meters ((8-15-17 right angled triangle).
The configuration, when they see each other at the last time, is similar, but reversed, right angled (800-1500-1700 meters) triangle.
So, moving in parallel courses, they will see each other until they together will cover
2*1500 meters = 3000 meters = 3 kilometers cumulatively.
Let "v" be velocity under the question.
Then we have this equation for cumulative distance
0.25*8 + 0.25*v = 2*3 kilometers. (1)
Here 0.25 is 0.25 of an hour, or 15 minutes.
From equation (1),
0.25v = 2*3 - 0.25*8 = 6 - 2 = 4 kilometers,
v = = 1500 meters ((8-15-17 right angled triangle).
The configuration, when they see each other at the last time, is similar, but reversed, right angled (800-1500-1700 meters) triangle.
So, moving in parallel courses, they will see each other until they together will cover
2*1500 meters = 3000 meters = 3 kilometers cumulatively.
Let "v" be velocity under the question.
Then we have this equation for cumulative distance
0.25*8 + 0.25*v = 2*3 kilometers. (1)
Here 0.25 is 0.25 of an hour, or 15 minutes.
From equation (1),
0.25v = 2*3 - 0.25*8 = 6 - 2 = 4 kilometers,
v = 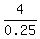 = 16 km/h. ANSWER
ANSWER. Velocity of the White Line ship is 16 kilometers per hour. = 16 km/h. ANSWER
ANSWER. Velocity of the White Line ship is 16 kilometers per hour.
Solved.
|
|
|