Question 1090435: A body travels half of its path length in last second of its free fall. Calculate the height from which it falls ?
Found 3 solutions by htmentor, Alan3354, ikleyn:
Answer by htmentor(1343)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let h = the fall height
Using the equation d = vt + 1/2gt^2, if the object falls half its height
in the final second, we can write:
h/2 = v*1 + g/2*1^2 = v + g/2
But the object falls a height of h/2 from rest to reach the speed v:
v^2 = v0^2 + 2gh/2 = gh [v0=0]
So we have two equations in two unknowns. Solve for h:
v^2 = gh
v = 1/2(h-g) -> v^2 = 1/4(h-g)^2
gh = 1/4(h^2 - 2gh + g^2)
h^2 - 6gh + g^2 = 0
The quadratic formula gives:
h = (6g +- sqrt(36g^2 - 4))/2
Using g = 9.81 m/s^2, we get:
h = 58.84 m and h = 0.017 m
The 2nd solution is unrealistic, so we take the 1st.
Ans: h = 58.84 m
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by ikleyn(52835)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A body travels half of its path length in last second of its free fall. Calculate the height from which it falls ?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
It is very well known fact from Physics, or from Calculus, or from your Algebra textbook,
that a free falling body falls the distance (the height)
H =  where t is the time of free falling counted from the very beginning time moment.
Let us find the time t based on the given condition.
Then your equation is
where t is the time of free falling counted from the very beginning time moment.
Let us find the time t based on the given condition.
Then your equation is
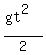 - - 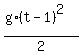 = = 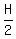 , or , or
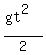 - - 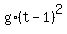 = = 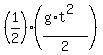 .
Now cancel the factor "g" in both sides. You will get the last equation in the form .
Now cancel the factor "g" in both sides. You will get the last equation in the form
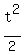 - - 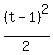 = = 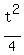 (*)
Since we excluded "g" from the equation, the solution for "t" does not depend on units we use
for the length or the distance (feet or meters).
Simplify the equation (*) (*)
Since we excluded "g" from the equation, the solution for "t" does not depend on units we use
for the length or the distance (feet or meters).
Simplify the equation (*)
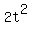 - - 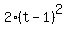 = =  , ,
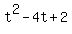 = 0.
The solution for t is (use the quadratic formula) = 0.
The solution for t is (use the quadratic formula)
 = = 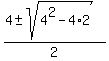 = = 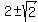 .
By the meaning of the condition, the value of "t" must be greater than 1 second, so only the root t = .
By the meaning of the condition, the value of "t" must be greater than 1 second, so only the root t = 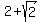 makes sense.
Then the height under the question is
H = makes sense.
Then the height under the question is
H =  = = 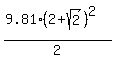 = 57.177 meters.
Check. Notice that = 57.177 meters.
Check. Notice that  = = 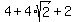 = = 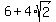 .
From the other side, .
From the other side, 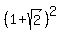 = = 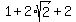 = = 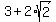 is exactly half of that. is exactly half of that.
Solved.
If you want to have the answer in feet, convert from meters to feet.
|
|
|