SOLUTION: A motor boat travels 204km in 4 hours going upstream. It travels 252km going downstream in the same amount of time. What is the rate of the boat in still water and what is the rate

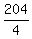 = 51  is the motor boat' speed relative to river's banks floating upstream.

It is the difference of the speed of the motor boat in still water "u" and the current speed "v". 
So you have this equation 

u - v = 51.    (1)


Next, 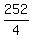 = 63  is the motor boat' speed relative to river's banks floating downstream.

It is the sum of the speed of the motor boat in still water "u" and the current speed "v".
So you have the second equation 

u + v = 63.    (2)

Hence, you need to solve the system of equation (1) and (2) to find "u" and "v":

u - v = 51.    (1')
u + v = 63.    (2')

Every time, when you see the system like this, add the equations (both sides). You will get

2u = 51 + 63  --->  2u = 114  --->  u = 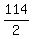 = 57.

It is the speed of the motor boat in still water, 57 . 

Now from (2) v = 63 - u = 63 - 57 = 6  is the speed of current.