Tutors Answer Your Questions about Travel Word Problems (FREE)
Question 1210382: Solve: 45x + 30 = 120
x = 12
x = 10
x = 6
x = 2
Found 3 solutions by Edwin McCravy, ikleyn, josgarithmetic:
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Solve: 45x + 30 = 120
x = 12
x = 10
x = 6
x = 2
I think that this student may have only gotten to the stage of finding
solutions by trial and error by substitution.
Try x = 12
45x + 30 = 120
45(12) + 30 = 120
540 + 30 = 120
570 = 120, so x = 12 is NOT the correct answer.
Try x = 10
45x + 30 = 120
45(10) + 30 = 120
450 + 30 = 120
480 = 120, so x = 10 is NOT the correct answer.
Try x = 6
45x + 30 = 120
45(6) + 30 = 120
270 + 30 = 120
300 = 120, so x = 6 is NOT the correct answer.
Try x = 2
45x + 30 = 120
45(2) + 30 = 120
90 + 30 = 120
120 = 120, so x = 2 IS the correct answer.
Edwin
Answer by ikleyn(52767)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Solve: 45x + 30 = 120
~~~~~~~~~~~~~~~~~~~~~~
It is a standard and typical linear equation in one unknown
for a beginner student to start learning the subject.
The standard mantra to solve is as follows:
subtract '30' from both sides. You will get
45x = 120-30,
45x = 90.
Now divide both sides by 45. You will get
x = 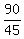 = 2.
ANSWER. The solution to given equation is x = 2.
CHECK. We substitute x= 2 into the left side of the given equation. It gives the value
45*2 + 30 = 90 + 30 = 120,
the same as the right side of the given equation.
This check CONFIRMS that the solution x = 2 is CORRECT. = 2.
ANSWER. The solution to given equation is x = 2.
CHECK. We substitute x= 2 into the left side of the given equation. It gives the value
45*2 + 30 = 90 + 30 = 120,
the same as the right side of the given equation.
This check CONFIRMS that the solution x = 2 is CORRECT.
Solved, with explanations and explicit check.
Knowing the methodology, you can solve a million of other similar problems/equations.
Answer by josgarithmetic(39615)  (Show Source): (Show Source):
Question 1167590: Stanley practices his running, swimming and biking every day. During these practices he runs at 9 mph, bikes at 16 mph and swims at 2.5 mph. Yesterday he ran for half an hour longer than he swam, and his biking time was twice his running time. How long did Stanley run, swim, and bike yesterday if the total distance he covered was 64 miles?
(a) If Stanley swam for t hours yesterday, what was his running time?
(b) In terms of t, how long did Stanley bike yesterday?
(c) What distance did Stanley covered while swimming?
(d) What distance did Stanley covered while running?
(e) What distance did Stanley covered while biking?
(f) What was the total distance Stanley covered during practices in terms of t?
(g) Write the equation that will allow you to find the practice time.
(h) For how long did Stanley swim, run, and bike yesterday?
I know someone else asked this but the answers were wrong
Found 4 solutions by mccravyedwin, ikleyn, Edwin McCravy, MathTherapy:
Answer by mccravyedwin(406)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Ikleyn,
Why don't you solve some of these unsolved probablity and statistics problems?:
https://www.algebra.com/tutors/faq.mpl?action=show_questions&topic=Probability-and-statistics
They are all from 2020, when high schools and colleges started emphasizing
statistics and de-emphasizing other math subjects? This is just a few of them.
Are you like the other tutors, who don't like stats either?
You will notice that they are all numbered from 1166229 to 1167907, which means
they were posted in that magic year, 2020, when the site started on its downward
trend.
Solving stats problems is the only way to get this site back on its feet again.
Edwin
Answer by ikleyn(52767)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Explanation specially for Edwin:
Dear Edwin, the solutions which we produce at this forum at present time,
the solutions that we produced at this forum in the past,
and the solutions that we will produce at this forum in future,
will be used as a base of knowledge in tens cases when developers of AI
will develop their versions of AI.
From this point of view, it does not matter if a problem was posted
today, yesterday or 5 years ago, or even 15 years ago.
What really does matter for these developers is to have correct appropriate solutions
in the knowledge database, which is a collection of templates and is a fuel for the AI engines,
covering all required topics at all necessary levels.
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I posted an answer to problem number 1172392 back in December 27, 2020. This one
is numbered 1167590, which means it was posted even before that. That was back
before schools started emphasizing statistics when all the tutors stopped
posting answers to statistics problems.
I'm sure whoever posted it 4.5 years ago, is happy to see that someone finally
answered it 4.5 years later. J
Answer by MathTherapy(10549)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Stanley practices his running, swimming and biking every day. During these practices he runs at 9 mph, bikes at 16 mph and swims at 2.5 mph. Yesterday he ran for half an hour longer than he swam, and his biking time was twice his running time. How long did Stanley run, swim, and bike yesterday if the total distance he covered was 64 miles?
(a) If Stanley swam for t hours yesterday, what was his running time?
(b) In terms of t, how long did Stanley bike yesterday?
(c) What distance did Stanley covered while swimming?
(d) What distance did Stanley covered while running?
(e) What distance did Stanley covered while biking?
(f) What was the total distance Stanley covered during practices in terms of t?
(g) Write the equation that will allow you to find the practice time.
(h) For how long did Stanley swim, run, and bike yesterday?
I know someone else asked this but the answers were wrong
As requested, let time spent swimming, be t
Since he ran half an hour longer than he swam, then time spent running = t +  hr, or (t + .5) hrs
And, since his biking-time was twice his running-time, then biking time = 2(t + .5)
As his running, biking and swimming speeds were 9 mph, 16 mph, and 2.5 mph, respectively, running, biking and swimming
distances were 9(t + .5), 16(2)(t + .5), and 2.5t, respectively
As he covered 64 miles, in total, we get the following DISTANCE equation:
9(t + .5) + 16(2)(t + .5) + 2.5t = 64
9t + 4.5 + 32t + 16 + 2.5t = 64
43.5t = 43.5
Time spent swimming, or hr, or (t + .5) hrs
And, since his biking-time was twice his running-time, then biking time = 2(t + .5)
As his running, biking and swimming speeds were 9 mph, 16 mph, and 2.5 mph, respectively, running, biking and swimming
distances were 9(t + .5), 16(2)(t + .5), and 2.5t, respectively
As he covered 64 miles, in total, we get the following DISTANCE equation:
9(t + .5) + 16(2)(t + .5) + 2.5t = 64
9t + 4.5 + 32t + 16 + 2.5t = 64
43.5t = 43.5
Time spent swimming, or  a) He swam for t = 1 hour, and so, he ran for t + .5 = 1.5 hours
Based on everything that was done above, you should be able to answer all other questions posed.
a) He swam for t = 1 hour, and so, he ran for t + .5 = 1.5 hours
Based on everything that was done above, you should be able to answer all other questions posed.
Question 1168000: A certain airplane can maintain a speed, without the presence of wind, of 210 mi/h and goes in the direction N 30° E. A wind is blowing west at 30 mi/h. Determine the final bearing of the plane and its ground speed. Calculate the speed in mi/h and the bearing in degrees.
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52767)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In January, February, March and April of 2025, @CPhill (which is the synonym of the Google AI)
posted 1941 solved problems to this forum.
He posted them at the rate of 25-30 solved problems per day.
Some of them (many of them) were solved incorrectly.
During these months, I tried to check the incoming problems, but, surely, been a human, not a
computer tool, I was not able to check all of them at the same rate.
Therefore, starting from the end of April 2025, and during May and June 2025, I checked
the remaining problems- those of them where I was competent to check.
I did not check the advanced Statistics problems, since I am not an expert in this field.
I also did not check advanced Finance problems, where I am not an expert.
But I checked a lot of other problems.
So, this file below contains the list of problems that (in my opinion) are solved incorrectly by @CPhill.
This list contains 151 incorrectly solved problems, so far.
For most of them, I placed my correct solutions.
Now some statistical counts.
As I said, the full number of solutions posted by @CPhill was 1941.
Of them, a huge portion were advanced statistics problems, which I did not check.
Their number was 2/3 or 3/4 of all problems - I did not count them.
Also, I did not check advanced Finance problems.
I think (I estimate approximately) that I checked from 500 to 600 problems,
As I said, so far the number of incorrect solutions is 151.
This number 151 does not cover all erroneous solutions by @CPhill - the number
of his erroneous solutions is more: I could miss some of them.
But this ratio "wrong to checked" = "151 to 500 or to 600" is HUGE.
It characterizes the level of this modern/contemporary version of this AI.
********************************************
Surely, it is unacceptable level for an AI.
********************************************
I am not an enemy to AI. But I want we all have right/correct understanding of what is the AI now
in solving school Math problems.
So, I hope that this my huge work on checking this AI is useful both for visitors of this site,
as well as for the developers of this AI.
Probably, in the future I will return to this checking, and then this list of erroneously solved problems will become greater.
ikleyn
June 29, 2025
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
The list of problems solved incorrectly by @CPhill
=====================================================
1208643
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1208643.html
We call a number cozy if every digit in the number is either a $3$ or next to a $3.$ For example, the numbers $333,$ $83,$ $303,$ and $3773$ are all cozy,
but the numbers $32423,$ $786,$ $340,$ and $3999$ are not cozy.
How many positive $10$-digit numbers are cozy?
1209502
https://www.algebra.com/algebra/homework/complex/Complex_Numbers.faq.question.1209502.html
Let be three positive numbers such that:
x^2 + y^2 + z^2 = 2(xy + xz + yz).
x + y + z + \frac{1}{xyz} > 4.
1209450
https://www.algebra.com/algebra/homework/complex/Complex_Numbers.faq.question.1209450.html
A triangle ABC, where |AB| = |AC|, a line CD is drawn from angle C and intersects side AB at D, such that |AD| = |CD| = |BC|.
Find the measure of angle A in degrees.
1193410
https://www.algebra.com/algebra/homework/playground/test.faq.question.1193410.html
Julita owes Jose the following am
a. 55,000 at the end of 4 years,
b. 48,000 at the end of 5 years, and
c. 75,000 due in 3 years from today at 9% converted quarterly.
What single payment at the end of 2 years will settle Julita’s
obligations if money is worth 15% converted monthly?
1193440
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1193440.html
A shipment of 10 items has two defective and eight non defective units. In the inspection of the shipment , a sample of units will be selected and tested.
If a defective unit is found , the shipment of 10 units will be rejected.
If a sample of four is selected , what is the probability that the shipment will be rejected?
1192630
https://www.algebra.com/algebra/homework/playground/lessons/test.faq.question.1192630.html
the semiannual withdrawals possible over 4.5 years from an account earning 5.25% compounded semiannually
and starting with $11,000. (Round your answer to the nearest cent.)
1192634
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1192634.html
In the movie Forrest Gump, the public school required an IQ of at least 80 for admittance.
IQ test scores are normally distributed with mean 100 and standard deviation 16
a. What percentage of people would qualify for admittance to the school.
b. If the public school wishes 95 percent of all children to qualify for admittance,
what minimum IQ test score should be required for admittance?
1209484
https://www.algebra.com/algebra/homework/Surface-area/Surface-area.faq.question.1209484.html
Trapezoid ABCD has diagonals that cross at E. The area of triangle EDC is n².
If AB has length m and DC has length n, find the area of trapezoid ABCD in terms of m and n.
Diagram: https://ibb.co/svwxc0w
1192431
https://www.algebra.com/algebra/homework/coordinate/word/Linear_Equations_And_Systems_Word_Problems.faq.question.1192431.html
you are given 20 true false questions and required to find probability of almost 4 are correct?
1192508 (10)
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1192508.html
A breathalyser test is used by police in an area to determine whether a driver has an excess of alcohol in their blood.
The device is not totally reliable: 7 % of drivers who have not consumed an excess of alcohol give a reading from the breathalyser
as being above the legal limit, while 10 % of drivers who are above the legal limit will give a reading below that level.
Suppose that in fact 14 % of drivers are above the legal alcohol limit, and the police stop a driver at random.
Give answers to the following to four decimal places.
Part a)
What is the probability that the driver is incorrectly classified as being over the limit?
Part b)
What is the probability that the driver is correctly classified as being over the limit?
Part c)
Find the probability that the driver gives a breathalyser test reading that is over the limit.
Part d)
Find the probability that the driver is under the legal limit, given the breathalyser reading is also below the limit.
1192522
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1192522.html
It is estimated that approximately 8.37% Americans are afflicted with diabetes. Suppose that a certain diagnostic evaluation for diabetes
will correctly diagnose 98% of all adults over 40 with diabetes as having the disease and incorrectly diagnoses 3% of all adults over 40
without diabetes as having the disease.
a) Find the probability that a randomly selected adult over 40 does not have diabetes, and is diagnosed as having diabetes
(such diagnoses are called "false positives").
b) Find the probability that a randomly selected adult of 40 is diagnosed as not having diabetes.
c) Find the probability that a randomly selected adult over 40 actually has diabetes, given that he/she is diagnosed as not having diabetes
(such diagnoses are called "false negatives").
(Note: it will be helpful to first draw an appropriate tree diagram modeling the situation)
1209504
https://www.algebra.com/algebra/homework/word/misc/Miscellaneous_Word_Problems.faq.question.1209504.html
Jamie spent 3/4 of her money on 3 books of the same price. Grace spent 5/9 of her money on 2 diaries.
They were each left with an equal amount of money. One book cost $3.30 more than one diary.
How much money did they have altogether.
1192298
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1192298.html%20algebra.com
Find the number of permutations of 10 numbers in a spinner.
1192052
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1192052.html
Triplets Peter, Reeta and Nikita have two ways for getting home from school each day: cycle on a tandem bike or walk.
The bike can carry either one or two riders at a time. Regardless of the number of people pedalling, cycling speed
is 5 times walking speed. The triplets always leave school at the same time and always use the same path between school
and home, whether walking or cycling. The school is 5 km from home and their walking speed is 4 kilometres per hour.
a) On Monday, Nikita and Peter cycle and Reeta walks. On reaching the point four-fifths of the way home the bike gets a puncture,
so Nikita and Peter walk the rest of the way home. How far from school is Peeta when the cyclists arrive home?
b) On Tuesday, Peter and Reeta ride the bike and Nikita walks. When the cyclists arrive home, Peter hops off the bike and Reeta rides back
towards school to collect Nikita. How far from school is Nikita when Reeta reaches her?
c) On Wednesday, Reeta and Nikita take the bike and Peter walks. When the cyclists are halfway home, Reeta hops off and walks the rest of the way,
while Nikita heads back to pick up Peter. How far from school is Reeta when her siblings pass her on the bike?
d) On Thursday, it is Reeta's turn to walk. Peter drops Nikita off at a certain point leaving her to walk home. Meanwhile he returns to pick up Reeta
and they cycle home together. If all three arrive home at the same time, how far from school are the drop-off and pick-up points?
Part (d) is interpreted and solved INCORRECTLY by @CPhill.
1209514
https://www.algebra.com/algebra/homework/word/misc/Miscellaneous_Word_Problems.faq.question.1209514.html
There were 220 chickens, ducks and goats on a farm. The ratio of chickens to ducks and goats is 3 to 2. The ratio of goats to ducks and chickens
is 1 to 3. What is the ratio of chickens to ducks to goats. If a goat is sold at $98 each, Find the amount if all the goats are sold.
1209515
https://www.algebra.com/algebra/homework/word/misc/Miscellaneous_Word_Problems.faq.question.1209515.html
There were some oranges in baskets A B and C. The ratio of A to B and C is 1 to 4.
The ratio of C to A and B is 3 to 4.
How many oranges were in C if there were 54 more oranges in B than in A.
1209520
https://www.algebra.com/algebra/homework/Polygons/Polygons.faq.question.1209520.html
Square SQUR has sides of length x. If triangle SQE is equilateral, find the area of triangle QAU.
Link to diagram: https://ibb.co/C58rZ09R
1192249
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1192249.html
Hotel A and B offers 2 types of packages that include lodging only or lodging with
breakfast. From a group of 300 tourists, 30 tourist choose Hotel A for lodging only
and 120 tourists choose Hotel B for lodging with breakfast.
Altogether 110 tourists choose to stay in Hotel A.
A tourist is selected randomly.
(a) What is the probability that the tourist chooses Hotel A or tourists chooses lodging only?
(b) What is the probability that the tourist to choose Hotel B for lodging with breakfast, if he chose Hotel B?
(c) What is the probability that the tourist to choose Hotel A, if he chose lodging without breakfast?
(d) What is the probability that the tourist chose Hotel A without breakfast or choose Hotel B with breakfast?
1192250
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1192250.html
Hotel A and B offers 2 types of packages that include lodging only or lodging with
breakfast. From a group of 300 tourists, 30 tourist choose Hotel A for lodging only
and 120 tourists choose Hotel B for lodging with breakfast.
Altogether 110 tourists choose to stay in Hotel A.
A tourist is selected randomly.
(a) What is the probability that the tourist chooses Hotel A or tourists chooses lodging only?
(b) What is the probability that the tourist to choose Hotel B for lodging with breakfast, if he chose Hotel B?
(c) What is the probability that the tourist to choose Hotel A, if he chose lodging without breakfast?
(d) What is the probability that the tourist chose Hotel A without breakfast or choose Hotel B with breakfast?
1209524 (20)
https://www.algebra.com/algebra/homework/Circles/Circles.faq.question.1209524.html
Sector ABC is 1/12 of a circle with diameter 24k. Line segment AD is perpendicular to segment BC.
Find the area of the shaded region.
Link to diagram: https://ibb.co/5gNwX0K6
1191371
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1191371.html
Suppose you want to have $600,000 for retirement in 30 years. Your account earns 10% interest.
How much would you need to deposit in the account each month?
1190652
https://www.algebra.com/algebra/homework/word/finance/Money_Word_Problems.faq.question.1190654.html
What is the present value of an ordinary annuity having semi-annual payments
of 8, 000 pesos for 12 years with an interest rate of 12% compounded annually?
1209532
https://www.algebra.com/algebra/homework/Circles/Circles.faq.question.1209532.html
Point R is chosen on the circumference of a circle and arc PQ is drawn with R as its center.
If P and Q are joined, the line segment formed is a diameter of the circle with length 2r cm.
Find the area of the shaded region in terms of r, in square centimeters.
Link to diagram: https://ibb.co/GQFdy2SV
1186907
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1186907.html
The world production of gold from 1970 to 1990 can be modelled by G = 5.2t 2 - 76t + 1492, where G is the
number of tonnes of gold and t is the number of years since 1970, t = 1 for 1971 and so on.
a. What was the most amount of gold mined in one year?
b. How much gold was mined in 1978?
1186928
https://www.algebra.com/algebra/homework/word/misc/Miscellaneous_Word_Problems.faq.question.1186928.html
For each of the following statements, explain why it is true for all functions f and g or give
an example of specific functions f and g showing that it is false.
a. All elements in the domain of g must be in the domain of f o g (fog)
b. All elements in the range of f must be in the range of f o g
1187156
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1187156.html
During the scholarship examination of a certain scholarship grant taken by 10,000 applicants,
Donnabelle's score was 350 greater than the scores of 8995 applicants who took the examination.
What is the percentile of Donnabelle's score?
1209553
https://www.algebra.com/algebra/homework/playground/test.faq.question.1209553.html
If x + (24)^(⅓) = (16)^(⅓) + (36)^(⅓)
find (10³/x⁶) - (x³/10³) - (30/x³)
1186854
https://www.algebra.com/algebra/homework/Length-and-distance/Length-and-distance.faq.question.1186854.html
Two vertices of a regular quadrilateral are A(0,4) and B(0,24). Which of the following could be the other two vertices?
a. C(4,4) and D(4,24)
b. C(24,4) and D(24,24)
c. C(8,24) and D(8,4)
d. C(0,8) and D(0,28)
1186205
https://www.algebra.com/algebra/college/linear/Linear_Algebra.faq.question.1186205.html
The Intellectual Company produces a chemical solution used for cleaning carpets.
This chemical is made from a mixture of two other chemicals which contain cleaning agent X and cleaning agent Y.
Their product must contain 175 units of agent X and 150 units of agent Y and weigh at least 100 pounds.
Chemical A costs ₱ 8 per pound, while chemical B costs ₱ 6 per pound.
Chemical A contains one unit of agent X and three units of agent Y.
Chemical B contains seven units of agent X and one unit of agent Y.
a. Set up the following:
i. Variables
ii. Constraints
iii. Objective Function
b. Find the minimum cost
c. Determine the best combination of the ingredients to minimize the cost.
1186248 (30)
https://www.algebra.com/algebra/college/linear/Linear_Algebra.faq.question.1186248.html
The Intellectual Company produces a chemical solution used for cleaning carpets.
This chemical is made from a mixture of two other chemicals which contain cleaning agent X and cleaning agent Y.
Their product must contain 175 units of agent X and 150 units of agent Y and weigh at least 100 pounds.
Chemical A costs ₱ 8 per pound, while chemical B costs ₱ 6 per pound.
Chemical A contains one unit of agent X and three units of agent Y.
Chemical B contains seven units of agent X and one unit of agent Y.
a. Set up the following:
i. Variables
ii. Constraints
iii. Objective Function
b. Find the minimum cost
c. Determine the best combination of the ingredients to minimize the cost.
1186455
https://www.algebra.com/algebra/homework/word/finance/Money_Word_Problems.faq.question.1186455.amp
On her recent birthday, April 22, 2001, Nicole was given by her mother a certain sum of money as birthday present.
She decided to invest the said amount on 20% exact simple interest. If the account will mature
on Christmas day at an amount of P 10,000.00, How much did Nicole receive from her mother on her birthday
1186235
beginning at the origin a spiral is constructed from three semmi-circles with centres at (1,0), (0,0) and (2,0)
the area of the shaded region in u^2 is?
https://drive.google.com/file/d/1OLUZW44XSyKqEXVuIhuwpkMDvT8E14xU/view?usp=sharing
1186272
https://www.algebra.com/algebra/homework/Length-and-distance/Length-and-distance.faq.question.1186272.html
On a wall, 60 1/2 cm wide, Oscar is going to hang three pictures beside each other, each measuring 9 1/3 cm wide.
He will leave 3 1/2 cm in between each pair of adjacent pictures. He plans to use two nails to hang each picture,
and will centre these nails leaving 4 cm between each pair. How far, in cm, from the end of the wall(on either side)
will the first nail be placed?
1209558 <<<---=== solution for (a) is incorrect. solution for (c) is incorrect.
https://www.algebra.com/algebra/homework/playground/test.faq.question.1209558.html
a) If 7^sin²x - 7^cos²x = 8
find the value of x.
b) Let m be a given real number, Find all complex numbers x such that,
([x/(x+1)]² + [x/(x-1)]² = m² + m
c) ab = ½, bc = ⅓, ac = 1/6,
find (1/a²) + (1/b²) + (1/c²)
d) 2^x - 3^y = 5
2^(x+2) + 3^(y+2) = 59.
find xy
e) find m,
9^4^m = 4^9^m
f) (7^log₈x)×(x^log₉x) = 3969,
find x.
1186068
Suppose events A and B are independent and
P(A) = 1/4
P(B) = 1/5
Find the probability. (Enter the probability as a fraction.)
_____
P(A ∩ B) the line is above a and b only
1186121
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1186121.html
Tickets for a raffle cost $12. There were 713 tickets sold. One ticket will be randomly selected as the winner,
and that person wins $1800 and also the person is given back the cost of the ticket.
For someone who buys a ticket, what is the Expected Value (the mean of the distribution)?
1185780
https://www.algebra.com/algebra/homework/Graphs/Graphs.faq.question.1185780.html
The director of MIS Center At a large company wants to do stuff consulting station with two shifting teams:
Team A will compromise of 3 senior programmers and 3 system analyst and
team B will consist 2 senior programmers and 5 system analysts.
the director wants to use no more than 42 individuals.
There will be at least 48 hours to be filed during the week, with team A serving for 4 hours and the team B shift servings for 3 hours.
The cost of team A is 3200 per hour and 2800 per hour for team B shift.
Determine the number of shifts each team has to render in order to minimize the cost.
•What is the Test ratio for table 2?
•What is the pivotal/al column in Tableu 1?
•What is the result in the last row of Tableu 4?
•Show the proper representation of Tableu
1209595
https://www.algebra.com/algebra/homework/complex/Complex_Numbers.faq.question.1209595.html
limit x (1 - 2 cos ((pi x)/(3 x - sqrt3))) as x \[LongRightArrow] + \[Infinity]
1209654
https://www.algebra.com/algebra/homework/Systems-of-equations/Systems-of-equations.faq.question.1209654.html
Find the unique pair of real numbers (x,y) satisfying
(6x^2 - 18x + 17) + (3y^2 + 6y + 11) = 28
and x + y = 20.
1209644 (40)
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209644.html
Find all complex solutions to the equation z^8 + 144 = 25z^4 + 10z^6 + 10z^2.
1209645
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209645.html
Find all complex solutions to the equation z^8 + 16 = 17z^4 - 8z^6 - 8z^2.
1209660 <<<---=== the problem is posed incorrectly, and the answer by @CPhill is incorrect
https://www.algebra.com/algebra/homework/Quadratic-relations-and-conic-sections/Quadratic-relations-and-conic-sections.faq.question.1209660.html
Find the conic section represented by the equation
x^2 - 4x + y^2 = y^2 + 8x + 20
1209701
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209701.html
Find a monic quartic polynomial f(x) with rational coefficients whose roots include x = 2 - i \sqrt[3]{3}$.
Give your answer in expanded form.
1209688 <<<---=== Fake problem and wrong solution/answer by @CPhill
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209688.html
The polynomial
f(x) = x^3 + 10x^2 + 21x + 10 + 4x^3 - 17x^2 + 8x - 66
has one integer root. What is it?
1184157
https://www.algebra.com/algebra/homework/Distributive-associative-commutative-properties/Distributive-associative-commutative-properties.faq.question.1184157.html
Construct two examples of bijective function from ZxZ to Q where Z is set of all integers and Q is set
of rational numbers.
1184450
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1184450.html
A certain class has 11 students, 2 of whom are sisters. The class needs to be split across three rooms
for a socially distanced exam, where room A can seat 2 students, room B 3 students, and room C 6 students.
How many ways can the students be divided across the rooms, if the 2 sisters are not allowed to be in
the same room (say, for academic integrity) ?
1184115
https://www.algebra.com/algebra/homework/Percentage-and-ratio-word-problems/Percentage-and-ratio-word-problems.faq.question.1184115.html
Berlin and Cheryl had a total of 6750 stamps. At first, Andy have 50%
of his stamps to Berlin. Berlin then gave 1/3 of her stamps to Cheryl.
Finally, Cheryl gave 1/6 of her stamps to Andy. In the end, the ratio of the
number of Andy’s stamps to the number of Berlin’s stamps became 4:5.
Cheryl had twice the total number of stamps that Andy and Berlin had.
How many stamps did Berlin and Cheryl have in total at first?
1174471
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1174471.html
To save for retirement, Karla Harby put $500 each month into an ordinary annuity for 10 years.
Interest was compounded monthly. At the end of the 10 years, the annuity was worth $84,608.
What annual interest rate did she receive?
The interest rate she received was approximately ___%
1174826
https://www.algebra.com/algebra/homework/Quadratic-relations-and-conic-sections/Quadratic-relations-and-conic-sections.faq.question.1174826.html
find the equation of parabola which has contact of third order with the conic ax^2 +2hxy + by^2 +2gx +2fy +c =0 at origin.
1209808 (50)
https://www.algebra.com/algebra/homework/playground/test.faq.question.1209808.html
Find the value of θ,
sin(20°)*sin(θ) + sin(100°)*sin(20 - θ)° = 0
1209677
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209677.html
When g(x) is divided by x^2 - x - 6, the remainder is 2x + 7. What is the value
of g(8)?
1209710
https://www.algebra.com/algebra/homework/playground/lessons/test.faq.question.1209710.html
4^(1/√x) + 16^(1/√x) = 64^(1/√x)
1209712
https://www.algebra.com/algebra/homework/playground/test.faq.question.1209712.html
If (x√x)^(1/x) = 2, find x.
1181712
https://www.algebra.com/algebra/homework/quadratic/Quadratic_Equations.faq.question.1181712.html
A rocket is being launched vertically over a point 𝐴 on the ground with
a velocity of 550 𝑚𝑖Τℎ𝑟. Twenty five miles away from point 𝐴 on the
ground, there is a photographer video-taping the launch. At what rate
is the angle of elevation of the camera changing when the rocket
achieves an altitude of 25 miles?
1181729
https://www.algebra.com/algebra/homework/Volume/Volume.faq.question.1181729.html
The diameter of a sphere coincides with the axis of a right circular cone, and the surface of the cone intersects the surface of the sphere in in a great circle. Find
(a) the vertical angle of the cone:
(b) the volume of the cone;
(c) the volume common to the two solids:
(d) the volume of that portion of the cone which lies outside the sphere:
(e) the volume of that portion of the sphere which lies outside the cone. Denote radius of sphere by R.
Solve Problem if (a) R=2: (b) R=3.72.
1181730
https://www.algebra.com/algebra/homework/Volume/Volume.faq.question.1181730.html
The center of each of three spheres of radius R lies in the surfaces of the other two.
Pass a plane containing the centers of the spheres.
Find the area common to the three great circles cut from the spheres by this plane.
1181731
https://www.algebra.com/algebra/homework/Volume/Volume.faq.question.1181731.html
A sphere is inscribed in a right circular cone of altitude h and radius of base r.
Write a formula in terms of r and h for the volume of the sphere.
1181618
https://www.algebra.com/algebra/homework/word/travel/Travel_Word_Problems.faq.question.1181618.html
Modern oil tankers weigh more than a 1/2 million tons and have lengths up to one - fourth mile. Such massive ships require a distance of 5.0 km about (3.0 mi)
and a time of 20 minutes to come to a stop from top speed of 30 km/h.what is the magnitude of such ship's average acceleration in m/s squared in coming to a stop?
B. What is the magnitude of the ship's average velocity in m/s
1209741
https://www.algebra.com/algebra/homework/playground/test.faq.question.1209741.html
If 1/9^(1/x) + 1/3^(1/x) = 30,
find x.
1209729 (60)
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209729.html
Let t be a root of f(x) = x^3 - x + 3. Evaluate t^6 - 4t^5 + 7t^4 - 3t^2 + 10t - 13.
1209740
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209740.html
Factor x^2 - 2x - y^2 + 2yz + 5z^2 as the product of two polynomials of degree 1.
1209728
Let r, s, and t be solutions of the equation 3x^3 - 4x^2 - 2x + 12 = 0.
Compute (rs)/t^2 + (rt)/s^2 + (st)/r^2.
1209735
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1209735.html
69% of all Americans are home owners. If 37 Americans are randomly selected, find the probability that
a. Exactly 27 of them are are home owners.
b. At most 27 of them are are home owners.
c. At least 23 of them are home owners.
d. Between 23 and 28 (including 23 and 28) of them are home owners.
1209737
https://www.algebra.com/algebra/homework/word/misc/Miscellaneous_Word_Problems.faq.question.1209737.html
The dots on the opposite faces of a die have a sum of 7.
How many different sum of dots on three adjacent faces are there on a die?
1209731
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209731.html
Let r, s, and t be solutions of the equation x^3 + 2x^2 - 5x + 15 = 0. Compute
1/(r - 2s - 2t) + 1/(s - 2r - 2t) + 1/(t - 2r - 2s)
1180634
https://www.algebra.com/algebra/homework/equations/Equations.faq.question.1180634.html
This pandemic, Abheedette learned to bake while on home quarantine.
She also realized that she will be able to make P60.00 profit per tray of banana muffins
and P120.00 profit per tray of blueberry muffins.
She needs 2 cups of milk and 3 cups of flour to bake a tray of banana muffins.
And, baking a tray of blueberry muffins takes 4 cups of milk and 3 cups of flour.
She has 16 cups of milk and 15 cups of flour.
How many trays of each flavor must be baked to maximize the profit?
a. Define the variable used:
b. LP Model:
c. Identify the feasible region:
d. Corner Points and the objective functions:
e. Optimal Solution (final answer):
1209745
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209745.html
in the blanks, to complete the factorization:
(a^2 + b^2 - c^2)^2 - 4a^2 b^2 - 4a^2 c^2 + 4b^2 c^2 = (a + ___)(a + ___)(a + ___)(a + ___)
1180382
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1180382.html
a particle jumps between three positions A, B, and C. If it starts at A, it stays at A with probability 44%,
and it goes to B with probability 18% and to C with probability 26%. If, however, it starts at C, it goes to A with probability 51%
and to B with probability 16%.
Find the transition matrix.
If the particle stays at A, what is the probability that it stays at A after three jumps?
1179711
Determine the periodic payments on the given loan or mortgage.
$5,000,000 borrowed at 7% for 30 years, with quarterly payments
1179768 (70)
The problem on pendulum
https://gyazo.com/78c37f667cf2af63efadea4314e5642c
1179791
https://www.algebra.com/algebra/homework/Functions/Functions.faq.question.1179791.html
If the area (in square units) of the region under the curve of the function f(x) = 3x − 1 on t he interval [a, 4],
where a < 4, is 12 square units, identify all the possible values of a.
what values are correct?
a. -3
b. 0
c. -16/5
d. 8/3
e. -2
f. 7/2
1179819
https://www.algebra.com/algebra/homework/Sequences-and-series/Sequences-and-series.faq.question.1179819.html
Find the present values of the following annuities
i. RM6,000 every year for 8 years at 12% compounded annually
ii. RM800 every month for 2 years 5 months at 5% compounded monthly.
1179653 - about a pendulum, horizontal displacement.
https://gyazo.com/848645a235363970dae8196a58a2bbdc
1179602
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1179602.html
If 35% of the people in a community use the emergency room at a hospital one year.
Find these probabilities for a sample of 12 people
A) exactly 4 used the emergency room
B) At most 4 used the emergency room
C) At least 10 used the emergency room
1209768 <<<---=== incomplete solution: one solution is found; other solution is missed
https://www.algebra.com/algebra/homework/playground/lessons/test.faq.question.1209768.html
If a = sin50(1 + 2cos170°),
b = sin170°(1 + 2cos140°),
c = sin140°(1 + 2cos50°),
then (3 - 2A)ˣ = (x + 1)²,
find x
1209770 <<<---=== Total, global and fatal deceiving of a reader
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209770.html
Find all (real or nonreal) x satisfying
(x - 3)^4 + (x - 5)^4 = -8 + 6(x - 3)(x - 5)^3 - 11(x - 3)^3 (x - 5).
1179081 <<<---=== The problem is non-sensical. The solution by @CPhill is non-sensical, too.
https://www.algebra.com/algebra/homework/word/finance/Money_Word_Problems.faq.question.1179081.html
Nick has been depositing $190 in a savings account every three months for the past three years. This account paid 3 % convertible quarterly.
Nick has just made the last deposit. Nick is buying a car for $ 14000. He is taking out a car loan. He will use the accumulated value of his savings account
as the downpayment on the car. The loan is at 3 % convertible semiannually and has a term of 4 years. Find the size of Nick's monthly car loan payment.
1209773
https://www.algebra.com/algebra/homework/coordinate/Linear-systems.faq.question.1209773.html
If a_1, a_2, ..., a_19 satisfy
a_1 + a_2 + a_3 + a_4 = 1,
a_2 + a_3 + a_4 + a_5 = 2,
a_3 + a_4 + a_5 + a_6 = 3,
...
a_{16} + a_{17} + a_{18} + a_{19} = 16,
a_{17} + a_{18} + a_{19} + a_1 = 17,
a_{18} + a_{19} + a_1 + a_2 = 18,
a_{19} + a_1 + a_2 + a_3 = 19,
what is the value of a_19?
1178715
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1178715.html
Solve each problem.
1. Your monthly electric bill has a mean of ₱120.00. what is the percentage that you will pay an amount between ₱1,380 and ₱1,740?
2. Suppose the scores in the mathematics exam are normally distributed. If the exam has a mean score of 25 and a standard deviation of 5,what is the probability that if you take th
1178377 (80)
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1178377.html
Woofer Pet Foods produces a low-calorie dog food for overweight dogs. This product is made from beef products and grain. Each pound of beef costs $0.90,
and each pound of grain costs $0.60. A pound of the dog food must contain at least 9 units of Vitamin 1 and 10 units of Vitamin 2.
A pound of beef contains 10 units of Vitamin 1 and 12 units of Vitamin 2.
A pound of grain contains 6 units of Vitamin 1 and 9 units of Vitamin 2.
Formulate this as an LP problem to minimize the cost of the dog food. How many
pounds of beef and grain should be included in each pound of dog food? What is the cost and vitamin content of the final product?
1209775 <<<---=== AI produced the same wrong solution, kind of gibberish, and I reported to AI
https://www.algebra.com/algebra/homework/Systems-of-equations/Systems-of-equations.faq.question.1209775.html
Let a, b, c, and d be distinct real numbers such that
a = sqrt(4 + sqrt(5 + a)),
b = sqrt(4 - sqrt(7 + b)),
c = sqrt(4 + sqrt(9 - c)),
d = sqrt(4 - sqrt(11 - d)).
Compute abcd.
1209776 <<<---=== the "solution" by @CPhill is unreadable gibberish
https://www.algebra.com/algebra/homework/Systems-of-equations/Systems-of-equations.faq.question.1209776.html
Suppose the real numbers $a$, $b$, $x$, and $y$ satisfy the equations
ax + by = 3,
ax^2 + by^2 = 5,
ax^3 + by^3 = 17,
ax^4 + by^4 = 23.
Evaluate ax^5 + by^5.
See the solution at AoPS under this link
https://artofproblemsolving.com/wiki/index.php/1990_AIME_Problems/Problem_15?srsltid=AfmBOoq3eeok8NtsAuOBNtICcVv9fxgXqq0z4Tix5v0NoDfFL11W2Z72
1209790
https://www.algebra.com/algebra/homework/playground/test.faq.question.1209790.html
If x^x = 5, find x^x^(x+1).
1177476 <<<---=== part (a) was solved INCORRECTLY by @CPhill
https://www.algebra.com/algebra/homework/playground/test.faq.question.1177476.html
There are 150 people at an International Medical Conference.
40 are Africans, 70 are women and 110 are doctors.
12 of the women are Africans, 46 of the doctors are women and 31 of the Africans are doctors.
If 5 of the African men are not doctors:
(a) how many of the African women are doctors ?
(b) how many of the men are neither African nor doctors?
1177187
https://www.algebra.com/algebra/homework/Trigonometry-basics/Trigonometry-basics.faq.question.1177187.html
Owen is jumping on a trampoline. When his feet hit the deck of the trampoline, the material depresses
to a minimum height of 2cm. On average, Owen is reaching a maximum height of 200cm every 10 seconds.
Determine the equation of a sinusoidal function that would model this situation, assuming
Owen reaches his first maximum at 6 seconds.
1176885
https://www.algebra.com/algebra/homework/Graphs/Graphs.faq.question.1176885.html
If a simple, connected, graph has 20 vertices, what is the maximum number of edges it can have?
(Recall that a simple graph does not have loops and does not have multiple / parallel edges)
1176989
https://www.algebra.com/algebra/homework/Length-and-distance/Length-and-distance.faq.question.1176989.html
EVOL is a cyclic quadrilateral, inscribed in a circle with center S. Given that the radius of this circle
is 25 in. and angle VEL is 55 degrees, explain your work to find the following measurements.
a) Length of Major Arc VL
b) Angle measure of Minor Arc VL
c) Angle VOL
d) Length of Chord VL
1177001
https://www.algebra.com/algebra/homework/Circles/Circles.faq.question.1177001.html
EVOL is a cyclic quadrilateral, inscribed in a circle with center S. Given that the radius of this circle
is 25 in. and angle VEL is 55 degrees, explain your work to find the following measurements.
a) Length of Major Arc VL
b) Angle measure of Minor Arc VL
c) Angle VOL
d) Length of Chord VL
1176067 <<<---=== Inaccurate/icorrect calculations
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1176067.html
state lotto has a prize that pays $1,700 each week for 40 years.
Find the total value of the prize.
If the state can earn 3% interest on investments, how much money will they need to put
into an account now to cover the weekly prize payments?
1209804 (90)
https://www.algebra.com/algebra/homework/playground/test.faq.question.1209804.html
If sinx + sin²x + sin³x = 1,
find cos⁶x - 4cos⁴x + 8cos²x
1176479
https://www.algebra.com/algebra/homework/Circles/Circles.faq.question.1176479.html
Given seven equal circles on a hexagonal grid, how many permutations are possible where circles are always adjacent
(repetitions such as inversions and reflections excluded)?
1209808
https://www.algebra.com/algebra/homework/playground/test.faq.question.1209808.html
Find the value of θ,
sin(20°)*sin(θ) + sin(100°*sin(20 - θ)° = 0
1209794
(x+4)^2/9+(y+3)^2 /4 =1
1177711
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1177711.html
Roll a die once. Then roll it as many times as the outcome from the first roll.
Getting the special number "3" on any roll means a win.
What is the expected number of wins from this experiment?
1177712
A box has 3 red and 4 black balls. You randomly take one ball at a time without putting it back in.
Stop as soon as all the black balls are drawn out of the box. How many red balls do you expect to be left in the box?
(Hint: find the expected value of the properly defined random variable)
1209827
https://www.algebra.com/algebra/homework/Sequences-and-series/Sequences-and-series.faq.question.1209827.html
Find a closed form for S_n = 1!*(1^2 + 1) + 2!*(2^2 + 2) + . . . + n!*(n^2 + n)
for any integer n >= 1.
1209826
https://www.algebra.com/algebra/homework/Sequences-and-series/Sequences-and-series.faq.question.1209826.html
S_k = 1*(1^2) + 2!*(2^2)*3 + . . . + k*k!*(k + 1).
Find a closed form for S_k.
1173952
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1173952.html
A spheroid (or oblate spheroid) is a surface obtained by rotating an ellipse around its minor axis the ball
in figure 1.41 is in the shape of the lower half of a spheroid that is its horizontal cross-section as circles
well its vertical cross-section that pass through the center a semi-ellipse s if this bowl is 10 inch wide
at the opening and square root 10 in deep at the center how deep does a circular cover with diameter 9 in go into the bowl
1174226 <<<---=== what is presented by @CPhill as "the solution", is a complete gibberish.
https://www.algebra.com/algebra/homework/Average/Average.faq.question.1174226.html
A ladder 4m long at a construction site is resting against a wall. The bottom of the ladder is slipping away from the wall.
Find the estimate of the instantaneous rate of change of the Height H of the top of the ladder with respect to the Distance D
of the bottom of the ladder from the wall when the bottom of the ladder is 2.5m away from the wall.
Use h = 0.01 as the central interval.
1209832 (100)
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1209832.html
A body of weight 500N rests on a plane inclined at 20o to the horizontal. The coefficient of friction
is 0.4, determine a force F at an angle of 15o to the plane required to
(a) Pull the body upwards
(b) Push the body downwards
(c) Pull the body downwards
(d) Push the body upwards
1173392
In a school, every grade 10 student need to study 7 subjects out of 14. It is given that 4 of them are core subject,
and the rest are optional. How many arrangements of the subjects are available for the students?
1172965
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1172965.html
A certain household would like to buy a washing machine set payable for 6 months starting at the end of the month.
How much is the cost of the washing machine if the monthly payment amounts to $3000 and interest is 9% compounded semi-annually?
1172947
The Whittier Company needs to produce 40 units of Product A tomorrow. They can produce on either machine X or machine Y or both.
Each unit of Product A when pro cessed on machine X takes 30 minutes of time, while a unit processed on machine Y takes 25 minutes.
It costs the company $2 per minute and $3 per minute respectively to operate machines X and Y.
Tomorrow, machine X has only 10 hours available to produce Product A, while machine Y can be operated as long as desired.
Use the graphical method to deter mine how many hours to schedule on each machine to minimize production costs.
Draw the isocost lines corresponding to production costs of $2,500, $2,700, $3,000, and $3,500.
Which of the isocost lines result in a feasible but suboptimal solution: Which line is both feasible and optimal? Which is not feasible?
117902
In a class of 50 students 24 like football 21 basketball and cricket six like football and basketball 3 like basketball only,
five like all three games, and 14 did not like any of the three games.
1.illustrate this information of Venn diagram
2. Find the number of students who like
A. Football and cricket
B. Exactly one of the game
C. Exactly two of the game.
1172981
https://www.algebra.com/algebra/homework/word/misc/Miscellaneous_Word_Problems.faq.question.1172981.html
The Truth in Lending Law requires all lending institutions to fully disclose interest rates on all loans.
$5000 is loaned for 36 months with monthly payments of $162.50. Determine annual interest rate.
1171791
https://www.algebra.com/algebra/homework/word/finance/Money_Word_Problems.faq.question.1171791.html
a predator requires 21 units of food A 12 units of food B, and 21 units of food C as its average daily consumption.
these requirements are satisfied by feeling on two prey species.
one prey of species A, provides 6,2 and 3 units of food of A,B, and C, respectively.
to capture and digest a prey of species B provides 3,3 and 5 units of A, B and C, respectively.
to capture and digest a prey of species A requires 7 units of energy, on the average.
the corresponding energy.
How many preys of each should the predator capture to meet its food requirement with minimum expenditure?
find the objective function, constraints and max/min value.
1171394
27 % adults favor the use of unmanned drones by police agencies.
Twelve U.S. adults are randomly selected. Find the probability
that the number of U.S. adults who favor the use of unmanned drones by police agencies is
(a) exactly three,
(b) at least four,
(c) less than eight.
(a) P(3)=
1209876
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209876.html
Polynomials-and-rational-expressions/1209876: Find the largest value of x where the plots of
f(x) = - \frac{2x + 5}{x + 3} and g(x) = \frac{12}{x - 1}
1209874
https://www.algebra.com/algebra/homework/Systems-of-equations/Systems-of-equations.faq.question.1209874.html
Let (x,y,z) be the real solution to the system of equations
x + y = \sqrt{4z + 3}
y + z = \sqrt{4x - 1}
z + x = \sqrt{4y + 5}
Find x + y + z.
1171432 (110)
https://www.algebra.com/algebra/homework/logarithm/logarithm.faq.question.1171432.html
#1. Log2(3x-7)+log2(x+2)=log2(x+1) <<<---=== the solution is incorrect.
#2. Log2(3x+1)-log2(2-4x)>log2(5x-2)
1209929
https://www.algebra.com/algebra/homework/word/finance/Money_Word_Problems.faq.question.1209929.amp
The Pireras are planning to go to Europe 4 years from now and have agreed to set aside $180/month for their trip.
If they deposit this money at the en each month into a savings account paying interest at the rate of 3%/year
compounded monthly, how much money will be in their ‘travel fund at the end of the fourth year?
(Round your answer to the nearest cent.)
1209924
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209924.html
Let x_1, x_2, \dots, x_{100} be real numbers. If
x_1 + 2x_2 + \dots + 100x_{100} = 1,
then find the minimum value of x_1/1 + x_2/2 + \dots + x_{100}/100.
1209908
Let w, x, y, and z be positive real numbers. If w + 2x + 3y + 6z = 8 - w^2 - x^2 - y^2 - z^2,
then what is the maximum value of wxyz?
1170818
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1170818.html
A company claims to have invented a device that can measure the momentum of objects inside it with extreme
accuracy. The device fits within a matchbox, and the claimed precision with which it can measure momentum is
δp = ±10^−26kg ms^−1
Explain why the claimed performance cannot possibly be accurate, and estimate the smallest possible size of a
device with such momentum precision, according to laws of quantum physics.
1209937 <<<---=== the problem itself is SELF-CONTRADICTORY non-sensical gibberish
https://www.algebra.com/algebra/homework/Functions/Functions.faq.question.1209937.html
Let f be a function such that
f(xy) + x = xf(y) + f(x) + xy^2
for all real numbers x and y. If f(-1) = 3, then compute f(100).
1209938
https://www.algebra.com/algebra/homework/Functions/Functions.faq.question.1209938.html
Let f be a function such that
f(x) + f(2x + y) + 5xy = f(4x - y) - x^2 + 5xy - 8x + 17y + 1
for all real numbers x and y. Find f(10).
1209952
https://www.algebra.com/algebra/homework/Functions/Functions.faq.question.1209952.html
The function f(n) is defined for all integers n, such that
f(x) + f(y) = f(x + y) - 4xy - 1 + f(x^2) + f(y^2)
for all integers x and y, and f(1) = 1. Find f(n).
1209950
https://www.algebra.com/algebra/homework/Functions/Functions.faq.question.1209950.html
The function f(n) takes the integers to the real numbers such that
f(m + n) + f(m - n) = 2f(m) + 2f(n) + mn
for all integers m and n, and f(1) = 2. Find f(n).
1209949
https://www.algebra.com/algebra/homework/Functions/Functions.faq.question.1209949.html
The function f : \mathbb{R} \rightarrow \mathbb{R} satisfies
f(x)*f(y) - f(xy) = -2x - 6y + 10
for all x, y \in \mathbb{R}. Find f(x).
1209964 (120)
https://www.algebra.com/algebra/homework/Surface-area/Surface-area.faq.question.1209964.html
ACDF is a Parallelogram. DEF is a sector. ABC is a right triangle. Solve for the area of the composite figure.
https://ibb.co/MyW8MZ2P
1209959
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1209959.html
A club buys tickets for 15 seats in a row for a local production and then sends the tickets randomly
to the 15 people who ordered seats. Of these 15 people, 9 are actors and 6 are backstage workers.
Find the probability that:
(a) An actor and backstage worker will receive tickets sitting together.
(b) The actors will be seated together, and the backstage workers will be seated together.
1209960
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1209960.html
55% of all shark attacks are not fatal. Let r be the number of nonfatal attacks out of a random sample of five shark attacks.
(a) What is the probability all five shark attacks are nonfatal?
(b) What is the probability that three or more of the five shark attacks are nonfatal?
(c) What is the expected number of nonfatal shark attacks out of the five?
(d) What is the standard deviation of the r-probability distribution?
1210228
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1210228.html
Find the number of subsets of
S = \{1, 3, 8, 17, 30, 36, 47, 58\},
so that the sum of the elements in the subset is a multiple of 5.
(Note that for the empty subset, we take the sum of the elements as 0.)
1169789
https://www.algebra.com/algebra/homework/Trigonometry-basics/Trigonometry-basics.faq.question.1169789.html
Given a right pyramid ABCDE, on a square base ABCD, with AB = 8 cm, and height EO = 5 cm,
what are the values of the following:
(a) angle EAB
(b) angle β between a slant edge and the plane on the base.
(c) angle θ between a slant face and the plane on the base.
1210155
https://www.algebra.com/algebra/homework/Surface-area/Surface-area.faq.question.1210155.html
ABCE is a Parallelogram. ADEF is a Rhombus. Find the area of the composite figure.
https://ibb.co/Jj2jKPD3
1210151
https://www.algebra.com/algebra/homework/complex/Complex_Numbers.faq.question.1210151.html
In many ways can the letters of "lyltalqdr" be arranged such that no letter remains in its original position?
1168949
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1168949.html
A quilt is made up of strips of cloth, starting with an inner square
surrounded by rectangles to form successively larger squares.
The inner square and all rectangles have a width of 1 foot.
Write an expression using summation notation that gives the sum of
the areas of all the strips of cloth used to make the quilt shown.
Then evaluate the expression.
1168977
https://www.algebra.com/algebra/homework/Quadratic-relations-and-conic-sections/Quadratic-relations-and-conic-sections.faq.question.1168977.html
Conjugate axis along the y-axis, ome vertex at (0,7), asymptotes are 6x-5y+30=0 and 6x+5y-30=0.
Need help finding the Equation of this hyperbola. How?
1169051
https://www.algebra.com/algebra/homework/Sequences-and-series/Sequences-and-series.faq.question.1169051.html
The sample of work produced by lathe is 10000.
a. If the machine doubled this production every 20 minutes, how much will it produce
in one hour?
b. How long will it take the machine to produce 8 million?
1210173 (130)
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1210173.html
Let P be a point chosen uniformly at random inside triangle ABC. Extend ray BP to hit side AC at D.
What is the probability that BD < 4 ?
The sides of triangle ABC are 3, 5, and 7.
1210172
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1210172.html
Given a regular octagon, in how many ways can we color one diagonal red and another diagonal blue so that the two colored diagonals
intersect at an endpoint? Consider rotations and reflections distinct.
1210184
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1210184.html
I can only remember a seven-digit telephone number if the first three digits (the "prefix") are equal to the next
three digits or the last three digits. For example, I can remember 389-3892 and 274-9274.
How many seven-digit telephone numbers can I remember?
(For this problem, a telephone number cannot start with a 0.)
1210183
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1210183.html
In how many ways can we seat 3 pairs of siblings in a row of 10 chairs, so that nobody sits next to their sibling?
(Two chairs will be left empty, of course.)
1168409
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1168409.html
73% of all Americans live in cities with population greater than 100,000 people.
If 35 Americans are randomly selected, find the probability that
a. Exactly 26 of them live in cities with population greater than 100,000 people.
b. At most 26 of them live in cities with population greater than 100,000 people.
c. At least 25 of them live in cities with population greater than 100,000 people.
d. Between 21 and 25 (including 21 and 25) of them live in cities with population greater than 100,000 people.
1210201
https://www.algebra.com/algebra/homework/Length-and-distance/Length-and-distance.faq.question.1210201.html
Let ABCD be a square with side length 1. A laser is located at vertex A, which fires a laser beam at point X on side BC,
such that BX = 2/3. The beam reflects off the sides of the square, until it ends up at another vertex; at this point,
the beam will stop. Find the length of the total path of the laser beam. The diagram is linked below
https://artofproblemsolving.com/texer/zqcbfanp
1210212
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1210212.html
How many positive integers are there whose digits strictly decrease from left to right, and have at most one even digit,
and the sum of the digits is 6?
1210211
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1210211.html
How many positive integers are there whose digits strictly decrease from left to right, and have at most one even digit,
and the sum of the digits is 6?
1210210
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1210210.html
How many positive integers are there whose digits strictly decrease from left to right, and the sum of the digits is 6?
1210204
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1210204.html
Find the number of ways of arranging one A, two Bs, three Cs, and four Ds, so that no two Bs are next to each other,
no two Cs are next to each other, and no two Ds are next to each other.
1209733 (140)
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1209733.html
60% of all violent felons in the prison system are repeat offenders.
If 45 violent felons are randomly selected, find the probability that
a. Exactly 26 of them are repeat offenders.
b. At most 29 of them are repeat offenders.
c. At least 29 of them are repeat offenders.
d. Between 25 and 33 (including 25 and 33) of them are repeat offenders.
1168408
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1168408.html
64% of all violent felons in the prison system are repeat offenders.
If 48 violent felons are randomly selected, find the probability that
a. Exactly 28 of them are repeat offenders.
b. At most 30 of them are repeat offenders.
c. At least 32 of them are repeat offenders.
d. Between 28 and 34 (including 28 and 34) of them are repeat offenders.
1168513
https://www.algebra.com/algebra/homework/Systems-of-equations/Systems-of-equations.faq.question.1168513.html
Kent sold his car to Carolyn for $1,000 down and monthly payments of $120.03 at the end of every month
for 3 1/2 years. The interest rate charged is 12%, compounded monthly. What was the selling price of the car?
1210228
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1210228.html
Find the number of subsets of
S = \{1, 3, 8, 17, 30, 36, 47, 58\},
so that the sum of the elements in the subset is a multiple of 5. (Note that for the empty subset, we take the sum of the elements as 0.)
1209711
https://www.algebra.com/algebra/homework/playground/test.faq.question.1209711.html
[x-(1/x)]^(1/x) + [1-(1/x)] ^(1/x) = x
1209827
https://www.algebra.com/algebra/homework/Sequences-and-series/Sequences-and-series.faq.question.1209827.html
Find a closed form for
S_n = 1! \cdot (1^2 + 1) + 2! \cdot (2^2 + 2) + \dots + n! \cdot (n^2 + n).\]
for any integer n \ge 1. Your response should have a factorial.
1209826
https://www.algebra.com/algebra/homework/Sequences-and-series/Sequences-and-series.faq.question.1209826.html
For a positive integer k, let
S_k = 1 \cdot 1! \cdot 2 + 2 \cdot 2! \cdot 3 + \dots + k \cdot k! \cdot (k + 1).
Find a closed form for S_k.
1179819
https://www.algebra.com/algebra/homework/Sequences-and-series/Sequences-and-series.faq.question.1179819.html
Find the present values of the following annuities
i. RM6,000 every year for 8 years at 12% compounded annually
ii. RM800 every month for 2 years 5 months at 5% compounded monthly
1209870
https://www.algebra.com/algebra/homework/Functions/Functions.faq.question.1209870.html
Fill in the blanks.
(a) If f(x) is an even function and g(x) is an even function and h(x) is an even function, then f(x) + g(x) + h(x) is an ___ function.
(b) If f(x) is an odd function and g(x) is an odd function and h(x) is an even function, then f(x)*g(x) + h(x) is an ___ function.
(c) If f(x) is an even function and g(x) is an odd function and h(x) is an odd function, then f(x)*(g(x) + h(x)) is an ___ function.
(d) If f(x) is an odd function and g(x) is an even function and h(x) is an odd function, then f(x)*g(x)*h(x) is an ___ function.
The answer to (d) in the post by @CPhill is incorrect.
1209715
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209715.html
P(x) be a polynomial of the form
P(x) = 2x^3 + ax^2 - 23x + c,
such that 12 and 7 are roots of P(x). What is the third root?
For the polynomial in part (a), compute the ordered pair (a,c).
1190651 (150)
https://www.algebra.com/algebra/homework/word/finance/Money_Word_Problems.faq.question.1190651.html
What is the future value of an ordinary annuity having daily payments of 50 pesos for 30 days with an rate of 20% compounded daily?
1209897
https://www.algebra.com/algebra/homework/Rational-functions/Rational-functions.faq.question.1209897.html
Let x and y be real numbers satisfying
\frac{x^2y^2 - 1}{2y - 1} = 4x + y.
Find the largest possible value of x.
ikleyn
June 29, 2025
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Alright, let's break down this problem step by step to find the final bearing and ground speed of the airplane.
**1. Represent the Velocities as Vectors:**
* **Airplane's Velocity (relative to air, $\mathbf{v}_a$):**
* Magnitude: 210 mi/h
* Direction: N 30° E. This means 30° east of the north direction. In terms of a standard Cartesian coordinate system (where the positive x-axis is East and the positive y-axis is North), the angle with respect to the positive x-axis is $90^\circ - 30^\circ = 60^\circ$.
* Vector form:
$$\mathbf{v}_a = \langle 210 \cos(60^\circ), 210 \sin(60^\circ) \rangle = \langle 210 \cdot \frac{1}{2}, 210 \cdot \frac{\sqrt{3}}{2} \rangle = \langle 105, 105\sqrt{3} \rangle$$
* **Wind's Velocity ($\mathbf{v}_w$):**
* Magnitude: 30 mi/h
* Direction: West. This means it's along the negative x-axis.
* Vector form:
$$\mathbf{v}_w = \langle -30, 0 \rangle$$
**2. Determine the Ground Velocity ($\mathbf{v}_g$):**
The ground velocity of the airplane is the vector sum of its velocity relative to the air and the velocity of the wind:
$$\mathbf{v}_g = \mathbf{v}_a + \mathbf{v}_w = \langle 105, 105\sqrt{3} \rangle + \langle -30, 0 \rangle = \langle 105 - 30, 105\sqrt{3} + 0 \rangle = \langle 75, 105\sqrt{3} \rangle$$
**3. Calculate the Ground Speed (Magnitude of $\mathbf{v}_g$):**
The ground speed is the magnitude of the ground velocity vector:
$$|\mathbf{v}_g| = \sqrt{(75)^2 + (105\sqrt{3})^2} = \sqrt{5625 + 105^2 \cdot 3} = \sqrt{5625 + 11025 \cdot 3} = \sqrt{5625 + 33075} = \sqrt{38700}$$
$$|\mathbf{v}_g| \approx 196.72 \, \text{mi/h}$$
**4. Determine the Final Bearing (Direction of $\mathbf{v}_g$):**
The direction of the ground velocity vector can be found by calculating the angle it makes with the positive x-axis (East). Let this angle be $\alpha$.
$$\tan(\alpha) = \frac{\text{y-component}}{\text{x-component}} = \frac{105\sqrt{3}}{75} = \frac{7\sqrt{3}}{5} \approx 2.4249$$
$$\alpha = \arctan\left(\frac{7\sqrt{3}}{5}\right) \approx 67.65^\circ$$
This angle is measured counterclockwise from the positive x-axis (East). To express this as a bearing (relative to North or South), we need to convert it:
* Since the x-component (East) is positive and the y-component (North) is positive, the direction is in the Northeast quadrant.
* The angle with respect to the North direction is $90^\circ - \alpha$:
$$90^\circ - 67.65^\circ \approx 22.35^\circ$$
Since the angle is east of North, the final bearing of the plane is approximately N $22.35^\circ$ E.
**Summary of Results:**
* **Ground Speed:** Approximately $196.72$ mi/h
* **Final Bearing:** Approximately N $22.35^\circ$ E
Let me know if you'd like any part of this calculation explained in more detail!
Question 1170221: The volume and the total surface area of a spherical cone are 766 cu. cm. and 470 sq. cm., respectively. Find the vertex angle
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52767)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The volume and the total surface area of a spherical cone are 766 cu. cm. and 470 sq. cm., respectively. Find the vertex angle
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
For your info: " Spherical cone " is the same as " spherical horse in vacuum ",
an object for jokes in quantum mechanics :)
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! It appears that the term "spherical cone" is more accurately referred to as a "spherical sector." Therefore, we will approach this problem with that definition in mind.
Here's how we can approach solving this problem:
**Understanding Spherical Sectors**
* A spherical sector is a portion of a sphere defined by a conical boundary with its apex at the center of the sphere.
* To solve this problem, we'll need to use the formulas for the volume and surface area of a spherical sector.
**Formulas**
Let:
* R be the radius of the sphere.
* φ be the half-vertex angle of the spherical sector.
Then:
* Volume (V) = (2/3)πR³(1 - cos φ)
* Surface Area (A) = 2πR²(1 - cos φ) + πR²sin²(φ)
**Given Information**
* Volume (V) = 766 cu. cm.
* Surface Area (A) = 470 sq. cm.
**Solving the Problem**
1. **Relating Volume and Surface Area:**
* Notice that the first term in the surface area formula, 2πR²(1 - cos φ), is related to the volume formula. Specifically, 2πR²(1 - cos φ) = (3/R)V.
* Therefore we can make a substitution into the surface area equation.
2. **Substituting into the Surface area formula:**
* A = (3/R) * (V/2) + πR²sin²(φ)
* 470 = (3/R) * (766/2) + πR²sin²(φ)
* 470 = (1149/R) + πR²sin²(φ)
3. **Using volume to get a relationship:**
* 766 = (2/3)πR³(1 - cos φ)
4. **Difficulties and Simplification:**
* This problem is difficult to solve analytically. Therefore, a numerical method, or a calculator with a solve function would be very useful.
* It is also of note, that there may be a mistake in the given values, as they seem to lead to a very complex solution.
5. **Using approximations and focusing on the concept:**
* To give you the concept of how to solve this, if we could isolate R, and cos(phi), we could then solve for phi.
* However, without numerical methods, this is very difficult.
6. **Focusing on the concept of the vertex angle:**
* The vertex angle is 2 * phi.
* Therefore, once phi is found, it must be multiplied by 2.
**Conclusion**
Due to the complexity of the equations, solving this problem analytically is very difficult. A numerical method or a calculator with a solve function is recommended. If high accuracy is not needed, estimations could be made.
Question 1165646: An object is dropped from rest at a height of 118 m. Find the distance it falls during its final second in the air.
Answer by ikleyn(52767)   (Show Source): (Show Source):
Question 1168291: The world record for the 10,000 m run has been decreasing steadily since 1940. the function R(t)=30.18-0.06t estimates the record R, in minutes, as a function of t, the time in years since 1940. estimate the record for 2012
Answer by ikleyn(52767)   (Show Source): (Show Source):
Question 1165530: An engineer in a locomotive sees a car stuck
on the track at a railroad crossing in front of
the train. When the engineer first sees the
car, the locomotive is 160 m from the crossing
and its speed is 29 m/s.
If the engineer’s reaction time is 0.22 s,
what should be the magnitude of the minimum deceleration to avoid an accident?
Answer in units of m/s^2
.
Answer by ikleyn(52767)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
An engineer in a locomotive sees a car stuck on the track at a railroad crossing
in front of the train. When the engineer first sees the car, the locomotive
is 160 m from the crossing and its speed is 29 m/s.
If the engineer’s reaction time is 0.22 s, what should be the magnitude
of the minimum deceleration to avoid an accident?
Answer in units of m/s^2
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
In 0.22 of a second, the locomotive moves forward 29*0.22 = 6.38 meters.
The remaining distance to the car is 160 - 6.38 = 153.62 meters.
At the time moment t= 0.22 s, the locomotive starts decelerating.
We assume that the deceleration value remains constant.
At this condition, the average rate to the stop is 29/2 = 14.5 m/s.
Thus the time decelerating to the full stop is  = 10.59448276 seconds.
The uniform deceleration value is = 10.59448276 seconds.
The uniform deceleration value is  = 2.737273792.
ANSWER. The minimum uniform deceleration is about 2.74 m/s^2. = 2.737273792.
ANSWER. The minimum uniform deceleration is about 2.74 m/s^2.
Solved.
Question 1171404: Hi
Town P and town Q are 720km apart.Maggie & Andrew left town P at the same time. The average speed of Andrew was 40km per hour, Maggies was 60km per hour. As soon as they passed Point K which was 1/3 of the total distance,Maggie began to travel at a speed of 80km per hour. Both of them took the same number of hours to travel from town P to town Q.
How long did Maggie take to travel from town P to Point K.
What was Andrews speed from Point K to town Q.
Thanks
Found 2 solutions by MathTherapy, josgarithmetic:
Answer by MathTherapy(10549)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi
Town P and town Q are 720km apart.Maggie & Andrew left town P at the same time. The average speed of Andrew was 40km
per hour, Maggies was 60km per hour. As soon as they passed Point K which was 1/3 of the total distance, Maggie began
to travel at a speed of 80km per hour. Both of them took the same number of hours to travel from town P to town Q.
How long did Maggie take to travel from town P to Point K.
What was Andrews speed from Point K to town Q.
Thanks
It’s OBVIOUS that not only did Maggie increase her speed after getting to Point K, but Andrew did, as well.
Distance Maggie covered, from Point P to Point K:  of the 720-km distance: of the 720-km distance:  = 240 kms
Time Maggie took to get to Point K (240 kms): = 240 kms
Time Maggie took to get to Point K (240 kms):  = 4 hours
Remaining distance Maggie had to go (Point K to Q): 720 - 240 = 480 kms
Time Maggie took to go remaining distance (point K to Q), after increasing speed to 80 km/h: = 4 hours
Remaining distance Maggie had to go (Point K to Q): 720 - 240 = 480 kms
Time Maggie took to go remaining distance (point K to Q), after increasing speed to 80 km/h: 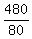 = 6 hours
Total time Maggie took to get from Point P to Q: 4 + 6 = 10 hours
Distance Andrew covered, from Point P to Point K: = 6 hours
Total time Maggie took to get from Point P to Q: 4 + 6 = 10 hours
Distance Andrew covered, from Point P to Point K:  of the 720-km distance: of the 720-km distance: 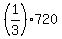 = 240 kms
Time Andrew took to get to Point K (240 kms): = 240 kms
Time Andrew took to get to Point K (240 kms):  = 6 hours
Remaining distance Andrew had to go (Point K to Q): 720 - 240 = 480 kms
Time Andrew took to go remaining distance (point K to Q), after increasing speed (S): = 6 hours
Remaining distance Andrew had to go (Point K to Q): 720 - 240 = 480 kms
Time Andrew took to go remaining distance (point K to Q), after increasing speed (S):  hours
Total time Andrew took to get from Point P to Q: hours
Total time Andrew took to get from Point P to Q:  hours
Since BOTH took the same amount of time to travel from P to Q, then each took 10 hours to complete the trip
We then get: Andrew’s ENTIRE-TRIP time = Maggie’s ENTIRE-TRIP time hours
Since BOTH took the same amount of time to travel from P to Q, then each took 10 hours to complete the trip
We then get: Andrew’s ENTIRE-TRIP time = Maggie’s ENTIRE-TRIP time

 ----- Factoring out GCF, 2, in numerator
3S + 240 = 5S ---- Multiplying by LCD, S
240 = 5S - 3S
240 = 2S ===> 2S = 240
Andrew’s speed from K to Q, or ----- Factoring out GCF, 2, in numerator
3S + 240 = 5S ---- Multiplying by LCD, S
240 = 5S - 3S
240 = 2S ===> 2S = 240
Andrew’s speed from K to Q, or 
Answer by josgarithmetic(39615)  (Show Source): (Show Source):
You can put this solution on YOUR website! Here is NOT a complete solution:
To reach point K, Maggie went 60 km per hour and distance  km. The time taken was km. The time taken was  hours. Maggie at point K was still 480 k.m. from point Q. hours. Maggie at point K was still 480 k.m. from point Q.
Question 1171450: The CN Tower in Toronto, Canada, is the tallest free-standing structure in North America. A woman on the observation deck, 1150 ft abouve the ground, wants to determine the distance between two landmarks on the ground below. She observes that the angle formed by the lines of sight to these two landmarks is 43°. She also observes that the angle between the vertical and the line of sight to one of the landmarks is 62° and that to the other landmark is 54°. Find the distance between the two landmarks.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step-by-step using trigonometry.
**1. Visualize the Situation**
Imagine the CN Tower as a vertical line. The woman is at the top, and the two landmarks are on the ground. We have a triangle formed by the woman and the two landmarks.
**2. Define Variables**
* Let the height of the observation deck be `h = 1150 ft`.
* Let the angle between the lines of sight to the landmarks be `θ = 43°`.
* Let the angle between the vertical and the line of sight to the first landmark be `α = 62°`.
* Let the angle between the vertical and the line of sight to the second landmark be `β = 54°`.
* Let the distance from the base of the tower to the first landmark be `d1`.
* Let the distance from the base of the tower to the second landmark be `d2`.
* Let the distance between the two landmarks be `D`.
**3. Calculate Distances to Landmarks (d1 and d2)**
We can use the tangent function to relate the height and distances:
* `tan(α) = d1 / h`
* `d1 = h * tan(α) = 1150 * tan(62°) ≈ 1150 * 1.8807 ≈ 2162.8 ft`
* `tan(β) = d2 / h`
* `d2 = h * tan(β) = 1150 * tan(54°) ≈ 1150 * 1.3764 ≈ 1582.9 ft`
**4. Apply the Law of Cosines**
Now, we have a triangle with sides `d1` and `d2`, and the angle between them is `θ = 43°`. We want to find the distance `D` between the landmarks. We can use the Law of Cosines:
* `D² = d1² + d2² - 2 * d1 * d2 * cos(θ)`
* `D² = (2162.8)² + (1582.9)² - 2 * 2162.8 * 1582.9 * cos(43°) `
* `D² ≈ 4677703.84 + 2505572.41 - 2 * 2162.8 * 1582.9 * 0.73135`
* `D² ≈ 7183276.25 - 5005813.1`
* `D² ≈ 2177463.15`
* `D ≈ √2177463.15 ≈ 1475.6 ft`
**Therefore, the distance between the two landmarks is approximately 1475.6 feet.**
Question 1171451: A water tower 30 m tall is located at the top of a hill. From a distance of 120 m down the hill it is observed that
the angle formed between the top and base of the tower is 8°. Find the angle of inclination of the hill; that is, the
angle that the slope of the hill makes with the horizontal.
Answer by ikleyn(52767)   (Show Source): (Show Source):
Question 1209809: Mark is involved in a cross country run and starts down the path at his normal pace; he usually covers 12 m in 2.0 s. After tying his shoelace for 15 s, Frank discovers that he has just given Mark a large lead. Nonetheless, Frank is faster at 6.5 m/s. Determine:
How long does it take Frank to catch Mark? (180 s)
If the race is 3 km in length, who finishes first and by what distance? (Frank, 140 m)
Answer by ikleyn(52767)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Mark is involved in a cross country run and starts down the path at his normal pace;
he usually covers 12 m in 2.0 s.
After tying his shoelace for 15 s, Frank discovers that he has just given Mark a large lead.
Nonetheless, Frank is faster at 6.5 m/s. Determine:
(a) How long does it take Frank to catch Mark? (180 s)
(b) If the race is 3 km in length, who finishes first and by what distance? (Frank, 140 m)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution for (a)
Mark' speed is 12/2 = 6 m/s; Frank' speed is 6.5 m/s.
Let "t" be the time for Frank to catch Mark.
Equate distances for Mark and for Frank
Mark Frank
6*(t+15) = 6.5*t.
Simplify and find t
6t + 90 = 6.5t
90 = 6.5t - 6t
90 = 0.5t
t = 90/0.5 = 180 seconds.
Frank will catch Mark in 180 seconds.
Solved.
Question 1177526: 1) At what Chicago local time is the chicago-frankfurt flight due to arrive in Frankfurt.
2)If it is 11:45am in Adelaide, what time is it in Moscow?
3) If it is 11:20am in Caracas what time is it in Auckland?
Departure Arrival City Time zone
Chicago 7:05pm* 2:45pm Chicago ST -6
Frankfurt ST +1
Caracas ST -4
Auckland ST 11
Adelaide ST 8.5
Moscow ST 3
*Previous Day ST: Summer Time
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! **1) Chicago to Frankfurt Arrival Time in Chicago Local Time**
* The flight arrives in Frankfurt at 2:45 pm Frankfurt local time.
* Frankfurt is ST +1, and Chicago is ST -6, so Frankfurt is 7 hours ahead of Chicago.
* To find the arrival time in Chicago local time, we subtract 7 hours from the Frankfurt arrival time: 2:45 pm - 7 hours = **7:45 am Chicago local time**.
**2) Time in Moscow when it's 11:45 am in Adelaide**
* Adelaide is ST +8.5.
* Moscow is ST +3.
* The time difference between Adelaide and Moscow is 8.5 - 3 = 5.5 hours.
* Since Adelaide is ahead of Moscow, we subtract 5.5 hours from the Adelaide time: 11:45 am - 5.5 hours = **6:15 am in Moscow**.
**3) Time in Auckland when it's 11:20 am in Caracas**
* Caracas is ST -4.
* Auckland is ST +11.
* The time difference between Caracas and Auckland is 11 + 4 = 15 hours.
* Since Auckland is ahead of Caracas, we add 15 hours to the Caracas time: 11:20 am + 15 hours = **2:20 am in Auckland (the next day)**.
Question 1177535: Questions:
1) At what Chicago local time is the chicago-frankfurt flight due to arrive in Frankfurt.
2)How long does the flight from Lisbon to Frankfurt take?
3) At what Shanghai local time is the Tokyo-frankfurt flight due to arrive in frankfurt?
INFO:
Leaving Departure Arrival City Time zone
Chicago 7:05pm* 2:45pm Chicago ST -6
Lisbon 7:35am 11.30am Frankfurt ST +1
Tokyo 12:30pm 8:45pm Shanghai ST +8
*Previous Day ST: Summer Time
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! **1) Chicago to Frankfurt Arrival Time in Chicago Local Time**
* The flight arrives in Frankfurt at 11:30 am Frankfurt local time.
* Frankfurt is ST +1, and Chicago is ST -6, so Frankfurt is 7 hours ahead of Chicago.
* To find the arrival time in Chicago local time, we subtract 7 hours from the Frankfurt arrival time: 11:30 am - 7 hours = **4:30 am Chicago local time**.
**2) Flight Duration from Lisbon to Frankfurt**
* The flight departs Lisbon at 7:35 am Lisbon local time.
* It arrives in Frankfurt at 11:30 am Frankfurt local time.
* Frankfurt is 1 hour ahead of Lisbon.
* To find the flight duration, we need to account for the time zone difference.
* 11:30 am Frankfurt time is 10:30 am Lisbon time.
* Therefore, the flight takes 10:30 am - 7:35 am = **2 hours and 55 minutes**.
**3) Tokyo to Frankfurt Arrival Time in Shanghai Local Time**
* The flight arrives in Frankfurt at 11:30 am Frankfurt local time.
* Shanghai is ST +8, and Frankfurt is ST +1, so Shanghai is 7 hours ahead of Frankfurt.
* To find the arrival time in Shanghai local time, we add 7 hours to the Frankfurt arrival time: 11:30 am + 7 hours = **6:30 pm Shanghai local time**.
Question 1177536: Questions:
1) At what Chicago local time is the chicago-frankfurt flight due to arrive in Frankfurt.
2)If it is 11:45am in Adelaide, what time is it in Moscow?
3) If it is 11:20am in Caracas what time is it in Auckland?
INFO:
Leaving Departure Arrival City Time zone
Chicago 7:05pm* 2:45pm Chicago ST -6
Lisbon 7:35am 11.30am Frankfurt ST +1
Tokyo 12:30pm 8:45pm Shanghai ST +8
Auckland ST +11
Adelaide ST +8.5
*Previous Day ST: Summer Time
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! **1) Chicago to Frankfurt Arrival Time in Chicago Local Time**
* The flight arrives in Frankfurt at 11:30 am Frankfurt local time.
* Frankfurt is ST +1, and Chicago is ST -6, so Frankfurt is 7 hours ahead of Chicago.
* To find the arrival time in Chicago local time, we subtract 7 hours from the Frankfurt arrival time: 11:30 am - 7 hours = **4:30 am Chicago local time**.
**2) Time in Moscow when it's 11:45 am in Adelaide**
* Adelaide is ST +8.5.
* Moscow is currently on Moscow Standard Time (MSK), which is UTC+3.
* The time difference between Adelaide and Moscow is 8.5 - 3 = 5.5 hours.
* Since Adelaide is ahead of Moscow, we subtract 5.5 hours from the Adelaide time: 11:45 am - 5.5 hours = **6:15 am in Moscow**.
**3) Time in Auckland when it's 11:20 am in Caracas**
* Caracas is in Venezuela Time (VET), which is UTC-4.
* Auckland is ST +11.
* The time difference between Caracas and Auckland is 11 + 4 = 15 hours.
* Since Auckland is ahead of Caracas, we add 15 hours to the Caracas time: 11:20 am + 15 hours = **2:20 am in Auckland (the next day)**.
Question 1178658: Find the magnitude and direction of the resultant for Vq = 5 ms and Vp 6ms. with angle 120 degrees between the two lines.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down how to find the magnitude and direction of the resultant vector.
**1. Represent the Vectors:**
* **Vq:** Magnitude = 5 ms, Direction = 0 degrees (we can assume it's along the x-axis for simplicity).
* Vq = 5i + 0j
* **Vp:** Magnitude = 6 ms, Direction = 120 degrees.
* Vp_x = 6 * cos(120°) = 6 * (-1/2) = -3 ms
* Vp_y = 6 * sin(120°) = 6 * (√3 / 2) = 3√3 ms
* Vp = -3i + 3√3j
**2. Find the Resultant Vector (Vr):**
* Vr = Vq + Vp
* Vr = (5i + 0j) + (-3i + 3√3j)
* Vr = (5 - 3)i + (0 + 3√3)j
* Vr = 2i + 3√3j
**3. Find the Magnitude of the Resultant (||Vr||):**
* ||Vr|| = √(Vr_x² + Vr_y²)
* ||Vr|| = √(2² + (3√3)²)
* ||Vr|| = √(4 + 27)
* ||Vr|| = √31
* ||Vr|| ≈ 5.57 ms
**4. Find the Direction of the Resultant (θ):**
* θ = arctan(Vr_y / Vr_x)
* θ = arctan(3√3 / 2)
* θ = arctan(5.196 / 2)
* θ = arctan(2.598)
* θ ≈ 68.96 degrees
**Therefore:**
* **Magnitude of the Resultant:** √31 ms (approximately 5.57 ms)
* **Direction of the Resultant:** Approximately 68.96 degrees (measured counter-clockwise from the x-axis, or the direction of Vq).
Question 1178659: Aeroplane A has a velocity of (-10i + 10j). To a passenger on aeroplane A, an aeroplane B appears to be travelling with a velocity of (16i + 4j). Find the velocity of the aeroplane B.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's solve this step-by-step:
**Understanding Relative Velocity:**
* **Velocity of A (Va):** (-10i + 10j)
* **Velocity of B relative to A (Vb/a):** (16i + 4j)
* **Velocity of B (Vb):** We need to find this.
The formula for relative velocity is:
Vb/a = Vb - Va
**Solving for Vb:**
1. **Rearrange the formula:**
* Vb = Vb/a + Va
2. **Substitute the given values:**
* Vb = (16i + 4j) + (-10i + 10j)
3. **Combine like terms:**
* Vb = (16i - 10i) + (4j + 10j)
* Vb = 6i + 14j
**Therefore, the velocity of aeroplane B is (6i + 14j).**
Question 1178660: A ship is sailing south west with a speed of 16√2 km/h and a submarine is travelling with velocity of (20i + 15j) km/h.
(a) Find the velocity vector of the ship.
(b) Find the velocity of the ship relative to the submarine.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step-by-step:
**a) Find the Velocity Vector of the Ship:**
1. **Direction:** "South West" means the ship is moving at a 45-degree angle from both the South and West directions.
2. **Angle from East:** Since it's Southwest, the angle measured counter-clockwise from the positive x-axis (East) is 180° + 45° = 225°.
3. **Velocity Components:**
* x-component (Westward): 16√2 * cos(225°)
* y-component (Southward): 16√2 * sin(225°)
4. **Calculate Cosine and Sine:**
* cos(225°) = -√2 / 2
* sin(225°) = -√2 / 2
5. **Velocity Components:**
* x-component: 16√2 * (-√2 / 2) = -16
* y-component: 16√2 * (-√2 / 2) = -16
6. **Velocity Vector:** The velocity vector of the ship is (-16i - 16j) km/h.
**Therefore, the velocity vector of the ship is (-16i - 16j) km/h.**
**b) Find the Velocity of the Ship Relative to the Submarine:**
1. **Velocity of the Ship (Vs):** (-16i - 16j) km/h
2. **Velocity of the Submarine (Vu):** (20i + 15j) km/h
3. **Relative Velocity (Vs_relative_to_Vu):** Vs - Vu
* Vs_relative_to_Vu = (-16i - 16j) - (20i + 15j)
* Vs_relative_to_Vu = (-16i - 20i) + (-16j - 15j)
* Vs_relative_to_Vu = -36i - 31j
**Therefore, the velocity of the ship relative to the submarine is (-36i - 31j) km/h.**
Question 1178662: A stationary observer O observes a ship S at noon, at a point whose coordinates relative to O are (20, 15); the units are kilometres. The ship is moving at a steady 10 km/h on a bearing of 150 degrees.
a) Express its velocity as a colum vector.
b) Write down in terms of t, its position after t hours.
c) Hence, find the value of t when it is due East of O. How far is it from O at this instant?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step-by-step:
**a) Express the Velocity as a Column Vector:**
1. **Bearing:** The ship is moving on a bearing of 150 degrees. This means the angle measured clockwise from North is 150 degrees.
2. **Angle from East:** To express the velocity in terms of x (East) and y (North) components, we need the angle relative to the East axis. The angle from the East axis is 150 degrees - 90 degrees = 60 degrees clockwise from East.
3. **Velocity Components:**
* x-component (Eastward): 10 * cos(60°) = 10 * (1/2) = 5 km/h
* y-component (Southward): 10 * sin(60°) = 10 * (√3 / 2) = 5√3 km/h
4. **Column Vector:** Since the y-component is southward, it's negative.
* Velocity vector = [5, -5√3]
**Therefore, the velocity vector is [5, -5√3] km/h.**
**b) Position After t Hours:**
1. **Initial Position Vector:** The initial position is (20, 15), which can be written as a column vector [20, 15].
2. **Displacement Vector:** The displacement after t hours is the velocity vector multiplied by t: [5t, -5√3t].
3. **Position Vector:** The position at time t is the initial position plus the displacement: [20, 15] + [5t, -5√3t] = [20 + 5t, 15 - 5√3t].
**Therefore, the position after t hours is [20 + 5t, 15 - 5√3t].**
**c) Time When Due East of O and Distance:**
1. **Due East Condition:** When the ship is due East of O, its y-coordinate must be equal to the y-coordinate of O, which is 0.
* 15 - 5√3t = 0
* 5√3t = 15
* t = 15 / (5√3)
* t = 3 / √3
* t = √3 hours
2. **Position at t = √3:**
* x-coordinate: 20 + 5√3
* y-coordinate: 15 - 5√3(√3) = 15 - 15 = 0
* Position: [20 + 5√3, 0]
3. **Distance from O:** The distance is the x-coordinate since the y-coordinate is 0.
* Distance = 20 + 5√3 km
* Distance ≈ 20 + 5(1.732)
* Distance ≈ 20 + 8.66
* Distance ≈ 28.66 km
**Therefore:**
* **Time (t):** √3 hours (approximately 1.732 hours)
* **Distance:** 20 + 5√3 km (approximately 28.66 km)
Question 1181618: Modern oil tankers weigh more than a 1/2 million tons and have lengths up to one - fourth mile. Such massive ships require a distance of 5.0 km about (3.0 mi) and a time of 20 minutes to come to a stop from top speed of 30 km/h.what is the magnitude of such ship's average acceleration in m/s squared in coming to a stop?
B. What is the magnitude of the ship's average velocity in m/s
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52767)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Regarding the post by @CPhill . . .
Keep in mind that @CPhill is a pseudonym for the Google artificial intelligence.
The artificial intelligence is like a baby now. It is in the experimental stage
of development and can make mistakes and produce nonsense without any embarrassment.
It has no feeling of shame - it is shameless.
This time, again, it looks like that this guy, @CPhill, even does not look at
and does not read what he posts, so his posts are often irrelevant or incorrect.
All @CPhill' solutions are copy-paste of Google AI solutions.
But there is one essential difference.
Every time, Google AI acknowledges at the end of its solutions that Google AI is experimental
and can make errors/mistakes.
All @CPhill' solutions are copy-paste of Google AI solutions,
but @CPhill never prints this acknowledge and never say that his solutions are copy-paste that of Google AI.
So, in my view, doing this way, this guy, @CPhill, simply makes dishonest business at this forum.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's a complete hypothesis test for the manufacturer's claim:
**a) Solution:**
We will use a two-sample z-test for the difference between means since the sample sizes are large (n > 30) and the population standard deviations are known.
**b) Parameter under study:**
The parameter under study is the difference between the average tensile strength of yarn A (μA) and the average tensile strength of yarn B (μB). We are interested in whether μA - μB < 12.
**c) Statement of Hypotheses:**
* Null hypothesis (H₀): μA - μB ≥ 12 (The difference is greater than or equal to 12 kg)
* Alternative hypothesis (H₁ or Ha): μA - μB < 12 (The manufacturer's claim: The difference is less than 12 kg)
**d) Significance level:**
α = 0.005
**e) Test statistic:**
The test statistic for a two-sample z-test is:
z = [(xA - xB) - (μA - μB)₀] / sqrt(σA²/nA + σB²/nB)
Where:
* xA and xB are the sample means
* (μA - μB)₀ is the hypothesized difference under H₀ (12)
* σA and σB are the population standard deviations
* nA and nB are the sample sizes
z = [(86.7 - 77.8) - 12] / sqrt((6.28²/50) + (5.61²/45))
z = [-3.1] / sqrt(0.788 + 0.700)
z = -3.1 / sqrt(1.488)
z ≈ -3.1 / 1.22
z ≈ -2.54
**f) Rejection region:**
Since this is a one-tailed test (less than), we look for the critical z-value that corresponds to α = 0.005 in the left tail of the standard normal distribution. Using a z-table or calculator, we find that the critical z-value is approximately -2.576.
The rejection region is z < -2.576.
**g) Decision making:**
Our calculated test statistic (z ≈ -2.54) falls *within* the rejection region (z < -2.576) .
Therefore, we *reject* the null hypothesis.
**h) Conclusion:**
There is sufficient evidence at the 0.005 significance level to support the manufacturer's claim that the average tensile strength of yarn A is less than the average tensile strength of yarn B by less than 12 kilograms.
Question 1181762: Modern Oil tankers weigh more than a half - million tons and have a length of up to one fourth - mile. Such massive ships require a distance of 5.0 km ( about 3.0 mi ) And a time of 20 minutes to come to a stop from top speed of 30 km/h
A. What is the magnitude of such a ship's average acceleration in m/s²
and coming to a stop ?
B. What is the magnitude of the ship's average velocity in m/s ?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to calculate the average acceleration and velocity:
**A. Average Acceleration**
1. **Convert units:**
* Initial speed (vᵢ) = 30 km/h * (1000 m/km) * (1 h/3600 s) = 8.33 m/s
* Final speed (v_f) = 0 m/s (since it comes to a stop)
* Time (t) = 20 minutes * (60 s/minute) = 1200 s
2. **Calculate average acceleration:**
Average acceleration (a) = (v_f - vᵢ) / t = (0 m/s - 8.33 m/s) / 1200 s ≈ -0.00694 m/s²
3. **Magnitude of acceleration:**
The magnitude is the absolute value of the acceleration. |a| ≈ 0.00694 m/s²
**B. Average Velocity**
1. **Calculate average velocity:**
Average velocity (v_avg) = (vᵢ + v_f) / 2 = (8.33 m/s + 0 m/s) / 2 ≈ 4.17 m/s
**Answers:**
* **A. Magnitude of average acceleration:** Approximately 0.00694 m/s²
* **B. Magnitude of average velocity:** Approximately 4.17 m/s
Question 1181806: A motorist goes for a drive, keeping the reading on the speedometer at a constant value of 40 km h−1. The speedometer is assumed to be accurate to ± 2 km h−1. At the end of the day he wants to know how far he has travelled, but unfortunately, he forgot to look at the distance indicator when he set out. He thinks that he drove for four hours, give or take a quarter of an hour. Estimate how far he travelled and assign an error to your result.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to estimate the distance traveled and its error:
1. **Nominal Distance:**
Distance = Speed × Time = 40 km/h × 4 h = 160 km
2. **Uncertainty in Speed:**
Δv = ± 2 km/h
3. **Uncertainty in Time:**
Δt = ± 0.25 h (15 minutes = 0.25 hours)
4. **Calculating the Uncertainty in Distance:**
Since distance is calculated by multiplying speed and time, the *fractional* uncertainties in speed and time combine to give the fractional uncertainty in distance.
(Δd/d)² = (Δv/v)² + (Δt/t)²
(Δd/d)² = (2/40)² + (0.25/4)²
(Δd/d)² = (0.05)² + (0.0625)²
(Δd/d)² = 0.0025 + 0.00390625 = 0.00640625
Δd/d = √0.00640625 ≈ 0.08
5. **Absolute Uncertainty in Distance:**
Δd = (Δd/d) * d = 0.08 * 160 km ≈ 12.8 km
6. **Final Result:**
The motorist traveled approximately 160 ± 13 km (rounded to two significant figures, consistent with the least precise measurement).
Question 1181807: The volume of the rectangular block in the figure is calculated from the following measurements of its dimensions: �10.00±0.10 cm, �5.00±0.06 cm and �4.00±0.04 cm. Calculate the error in the value of the volume of the block assuming: a) the errors are independent b) the errors are correlated such that they all push the estimate in the same direction.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to calculate the error in the volume, considering both independent and correlated errors:
**1. Calculate the Nominal Volume:**
V = lwh = (10.00 cm)(5.00 cm)(4.00 cm) = 200.00 cm³
**2. Fractional Uncertainties:**
* Δl/l = 0.10 cm / 10.00 cm = 0.01
* Δw/w = 0.06 cm / 5.00 cm = 0.012
* Δh/h = 0.04 cm / 4.00 cm = 0.01
**a) Independent Errors:**
When errors are independent, we add the *squares* of the fractional uncertainties and then take the square root.
1. Fractional uncertainty in volume:
(ΔV/V)² = (Δl/l)² + (Δw/w)² + (Δh/h)²
(ΔV/V)² = (0.01)² + (0.012)² + (0.01)²
(ΔV/V)² = 0.0001 + 0.000144 + 0.0001 = 0.000344
ΔV/V = √0.000344 ≈ 0.0185
2. Absolute uncertainty in volume:
ΔV = (ΔV/V) * V = 0.0185 * 200.00 cm³ ≈ 3.7 cm³
3. Volume with uncertainty:
V = 200.0 ± 3.7 cm³
**b) Correlated Errors:**
When errors are fully correlated (all pushing the estimate in the same direction), we simply *add* the fractional uncertainties.
1. Fractional uncertainty in volume:
ΔV/V = Δl/l + Δw/w + Δh/h
ΔV/V = 0.01 + 0.012 + 0.01 = 0.022
2. Absolute uncertainty in volume:
ΔV = (ΔV/V) * V = 0.022 * 200.00 cm³ = 4.4 cm³
3. Volume with uncertainty:
V = 200.0 ± 4.4 cm³
**Summary:**
* **Independent Errors:** V = 200.0 ± 3.7 cm³
* **Correlated Errors:** V = 200.0 ± 4.4 cm³
As expected, the uncertainty is larger when the errors are correlated because they all contribute to the error in the same direction. When independent, there is a chance that some errors cancel each other out, thus reducing the total uncertainty.
Question 1183038: A particle accelerates uniformly from rest at 0.15pi rad/s^2 from rest. The particle's initial position is at 45 degrees from the negative x-axis. If the particle moves a distance 15m along the arc of radius 2m for a time of 1.15 seconds, determine (a) position of the particle after 1.15 seconds from the +x-axis, (b) the initial and final angular velocity, (c) the tangential velocity and acceleration of the particle at 2 seconds.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve this rotational motion problem:
**(a) Position after 1.15 seconds:**
1. **Angular displacement (θ):** The particle travels a distance (s) of 15 m along an arc of radius (r) 2 m. The angular displacement is given by:
θ = s / r = 15 m / 2 m = 7.5 radians
2. **Initial position:** The initial position is 45 degrees from the negative x-axis. We need to convert this to radians measured counterclockwise from the positive x-axis:
* 45 degrees from the negative x-axis is equivalent to 180° + 45° = 225°
* 225° * (π/180°) = 5π/4 radians
3. **Final position:** The final position is the initial position plus the angular displacement:
* Final position = 5π/4 + 7.5 radians
* Final position ≈ 3.927 + 7.5 ≈ 11.427 radians
4. **Convert to degrees (optional):** If you want the final position in degrees:
* 11.427 radians * (180°/π) ≈ 654.7°
* To find the angle from the +x-axis, you may need to reduce this value to its principal value, by subtracting multiples of 360 until the value is between 0 and 360 degrees.
**(b) Initial and final angular velocity:**
1. **Initial angular velocity (ω₀):** The particle starts from rest, so ω₀ = 0 rad/s.
2. **Final angular velocity (ω):** We can use the following equation of rotational motion:
ω = ω₀ + αt
where α is the angular acceleration and t is the time.
ω = 0 + (0.15π rad/s²)(1.15 s)
ω ≈ 0.542 rad/s
**(c) Tangential velocity and acceleration at t = 2 s:**
1. **Angular velocity at t = 2 s:**
ω(t=2) = ω₀ + αt = 0 + (0.15π rad/s²)(2 s) ≈ 0.942 rad/s
2. **Tangential velocity (v):**
v = ωr = (0.942 rad/s)(2 m) ≈ 1.884 m/s
3. **Tangential acceleration (a_t):**
a_t = αr = (0.15π rad/s²)(2 m) ≈ 0.942 m/s²
4. **Radial (centripetal) acceleration (a_r):**
a_r = ω²r = (0.942 rad/s)²(2 m) ≈ 1.776 m/s²
5. **Total acceleration (a):** The total acceleration is the vector sum of the tangential and radial accelerations.
a = sqrt(a_t² + a_r²) = sqrt((0.942 m/s²)² + (1.776 m/s²)²) ≈ 2.00 m/s²
The direction of the total acceleration can be found using trigonometry:
angle = arctan(a_t / a_r) = arctan(0.942/1.776) ≈ 28 degrees from the radial direction.
**Summary of Results:**
* (a) Position after 1.15 seconds: ≈ 11.427 radians (or ≈ 654.7 degrees) from the +x-axis
* (b) Initial angular velocity: 0 rad/s; Final angular velocity (at 1.15 s): ≈ 0.542 rad/s
* (c) Tangential velocity at 2 s: ≈ 1.884 m/s
* (c) Tangential acceleration at 2 s: ≈ 0.942 m/s²
* (c) Total acceleration at 2 s: ≈ 2.00 m/s² at an angle of approximately 28 degrees from the radial direction.
Question 1185336: Anne drove her car to Laguna from Manila. She was at kilometer 20 when she noted that it was 9:00 AM and his speedometer indicated 50 km/h. At 9:30 AM, she saw his speedometer at 90 km/h and he was at kilometer 55. What is her acceleration (a) in km/hr/min? (b) in m/sec?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to calculate Anne's acceleration:
**(a) Acceleration in km/hr/min:**
1. **Calculate the change in velocity:**
Change in velocity (Δv) = Final speed - Initial speed
Δv = 90 km/h - 50 km/h = 40 km/h
2. **Calculate the change in time:**
Change in time (Δt) = 9:30 AM - 9:00 AM = 30 minutes
3. **Calculate the acceleration:**
Acceleration (a) = Change in velocity / Change in time
a = Δv / Δt
a = 40 km/h / 30 min
a = 4/3 km/hr/min or approximately 1.33 km/hr/min
**(b) Acceleration in m/s²:**
1. **Convert the change in velocity to m/s:**
Δv = 40 km/h * (1000 m/km) * (1 h/3600 s) = 100/9 m/s or approximately 11.11 m/s
2. **Convert the change in time to seconds:**
Δt = 30 min * 60 s/min = 1800 s
3. **Calculate the acceleration:**
a = Δv / Δt
a = (100/9 m/s) / 1800 s
a = 100 / (9 * 1800) m/s²
a = 1/162 m/s² or approximately 0.00617 m/s²
**Important Note:** The information about the distance traveled (from kilometer 20 to 55) is not needed to calculate the acceleration. Acceleration is solely determined by the change in velocity and the change in time.
Question 1185380: Anne drove her car to Laguna from Manila. She was at 20 km when she noted that it was 9:00 AM and his speedometer indicated 50 km/h. At 9:30 AM, she saw his speedometer at 90 km/h and he was at 55 km. What is her acceleration (a) in km/hr/min? (b) in m/sec?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to calculate Anne's acceleration:
**(a) Acceleration in km/hr/min:**
1. **Calculate the change in velocity:**
The change in velocity (Δv) is the difference between the final speed and the initial speed:
Δv = 90 km/h - 50 km/h = 40 km/h
2. **Calculate the change in time:**
The change in time (Δt) is the difference between the final time and the initial time:
Δt = 9:30 AM - 9:00 AM = 30 minutes
3. **Calculate the acceleration:**
Acceleration (a) is the change in velocity divided by the change in time:
a = Δv / Δt
a = 40 km/h / 30 min
a = 4/3 km/hr/min or approximately 1.33 km/hr/min
**(b) Acceleration in m/s²:**
1. **Convert the change in velocity to m/s:**
Δv = 40 km/h * (1000 m/km) * (1 h/3600 s) = 100/9 m/s or approximately 11.11 m/s
2. **Convert the change in time to seconds:**
Δt = 30 min * 60 s/min = 1800 s
3. **Calculate the acceleration:**
a = Δv / Δt
a = (100/9 m/s) / 1800 s
a = 100 / (9 * 1800) m/s²
a = 1/162 m/s² or approximately 0.00617 m/s²
Question 1185855: Two runners are running on circular tracks each of which has a circumference of
1320 feet. The tracks are 100 feet apart and the runners start opposite each
other and move at the same constant rate of 880 ft/min. How fast are the runners
separating when each has run 165 feet?
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52767)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I fully agree with Edwin in that the problem has too many uncertainties in its formulation.
The problem's formulation is at the amateur's level, not at the professional level.
More accurate formulations would be like this:
Two runners are running on circular tracks each of which has a circumference of
1320 feet. The tracks are 100 feet apart (the closest distance). The runners start
simultaneously from two closest points on the circles. One runner runs clockwise;
the other runner runs anti-clockwise. They move at the same constant rate of 880 ft/min.
How fast are the runners separating when each has run 165 feet?
The solution is quite simple.
First, notice that 165 feet is  = =  of the full circumference.
We can imagine that the centers of the circles are located on x-axis of a coordinate plane.
When the runners move 165 feet each, their corresponding position vectors will be
in position 45° and 135° to x-axis. So, the vectors of their speeds will be
u = (880*cos(45°),880*sin(45°)) for one runner,
and
v = (880*cos(135°),880*sin(135°)) for the other runner.
The difference of these vectors is u-v, i.e.
(880*cos(45°)-880*cos(135°),0).
So, the separating speed is of the full circumference.
We can imagine that the centers of the circles are located on x-axis of a coordinate plane.
When the runners move 165 feet each, their corresponding position vectors will be
in position 45° and 135° to x-axis. So, the vectors of their speeds will be
u = (880*cos(45°),880*sin(45°)) for one runner,
and
v = (880*cos(135°),880*sin(135°)) for the other runner.
The difference of these vectors is u-v, i.e.
(880*cos(45°)-880*cos(135°),0).
So, the separating speed is  , or approximately 880*1.4142 = 1244.5 ft/minute.
At this point, the problem is just solved completely.
ANSWER. The separation speed is , or approximately 880*1.4142 = 1244.5 ft/minute.
At this point, the problem is just solved completely.
ANSWER. The separation speed is  = 1244.5 ft/minute. = 1244.5 ft/minute.
Solved.
Notice that I solved the problem without using Calculus, despite of the Edwin' suggestion.
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
>>>Two runners are running on circular tracks each of which has a circumference
of 1320 feet. The tracks are 100 feet apart...
Does that mean their closest points are 100 feet apart?
>>>...and the runners start opposite each other...
Does that mean they are 100 feet apart, or at corresponding points on the
tracks?
>>>...and move at the same constant rate of 880 ft/min.
Are they both running the same direction, clockwise or counterclockwise, or is
one running clockwise and the other counterclockwise? That will make a
difference.
This is a related rates calculus problem. We could do it for all possibilities,
but to avoid waste, why not make it totally clear and repost?
Edwin
Question 1190090: Lara flies a helicopter over the well and drops a rope to measure her height above it. Exactly 125 m of rope is all she needs to touch the well; however, a steady wind is blowing the rope so it makes a straight line at an angle to the ground.
Meanwhile, back at the catapult, Harrison uses a rangefinder to determine that the helicopter is exactly 280 m away from the catapult, at an elevation of 15°.
Harrison radios Lara and confirms that the well, the helicopter and the catapult are all in the same vertical plane. Without making any further measurements, he now has enough information to set the distance for the catapult.
Harrison has one critical piece of information that you do not. Without it, you cannot determine the distance to the well with certainty. The information is not a measurement—Harrison will have no trouble determining it.
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52767)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Not a math problem.
More like puzzle or gum that is chewed in the mouth for a long time.
I do not understand, why and for what reason it was submitted to this forum.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! The critical piece of information Harrison has (and you don't) is the **angle of the rope**.
Here's why:
1. **Lara's Information:** Lara knows the length of the rope (125m). However, because the wind is blowing the rope at an angle, this is the *hypotenuse* of a right triangle. She *cannot* determine her vertical height above the well without knowing the angle of the rope.
2. **Harrison's Information:** Harrison knows the *straight-line distance* (280m) and *elevation angle* (15°) from the catapult to the helicopter. This allows him to calculate the *vertical height* of the helicopter above the ground.
3. **The Missing Link:** To connect Lara's information to Harrison's, you need to know the angle of the rope. This would allow Lara to calculate the vertical distance from the helicopter *down* to the well. Since Harrison has already figured out the helicopters height from the ground, the difference will give the distance from the catapult to the well.
**How Harrison Solves It:**
1. **Harrison calculates helicopter's height:** Using trigonometry (specifically the sine function), Harrison can find the helicopter's vertical height (h) above the ground: h = 280 * sin(15°).
2. **Lara calculates vertical distance to well:** With the rope's angle (let's call it 'θ'), Lara can calculate the vertical distance (v) from the helicopter to the well: v = 125 * cos(θ).
3. **Harrison calculates distance to well:** The vertical distance from the ground to the well is h - v. With this vertical distance and the horizontal distance from the catapult to the point directly below the helicopter (280cos15), Harrison can use the Pythagorean theorem to calculate the straight line distance from the catapult to the well.
Question 1192779: The sample space of a random experiment is {a, b, c, d, e, f}, and each outcome is equally likely. A random variable is defined as follows
Outcome a b c d e f
X 0 0 1.5 1.5 2 3
Determine the probability mass function of X.
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52767)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
This problem does not determine and does not prescribe any connection between
outcomes a, b, c, d, e, f and values of the random variable X.
What the problem asks, is to determine possible values of P(0), P(1.5), P(2) and P(3).
They can be any four arbitrary real values between 0 and 1;
the only restrictions is that their sum must be 1: P(0) + P(1.5) + P(2)+ P(3) = 1.
But the problem does not prescribe any relations between the outcomes a, b, c, d, d, f
and values of P.
So, in my view, the problem makes no sense, since its different parts
are not connected neither logically, nor physically one with another.
The post by @CPhill produces some semblance of a solution,
but how the problem itself is worded and posed - is NONSENSE.
My general impression is that in this post
two different problems are mistakenly mixed in one.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! The **probability mass function (PMF)** of a random variable \( X \) provides the probability of each possible value of \( X \). Here's how we determine the PMF:
### Step 1: Analyze the sample space and probabilities
The sample space is \( S = \{a, b, c, d, e, f\} \), and each outcome is equally likely. Since there are 6 outcomes:
\[
P(\text{each outcome}) = \frac{1}{6}.
\]
### Step 2: Group outcomes by the values of \( X \)
The random variable \( X \) assigns values to each outcome as follows:
- \( X(a) = 0 \),
- \( X(b) = 0 \),
- \( X(c) = 1.5 \),
- \( X(d) = 1.5 \),
- \( X(e) = 2 \),
- \( X(f) = 3 \).
We can group the outcomes by the values of \( X \):
- \( X = 0 \): Outcomes \( a, b \) → Probability = \( P(X = 0) = P(a) + P(b) = \frac{1}{6} + \frac{1}{6} = \frac{2}{6} = \frac{1}{3} \).
- \( X = 1.5 \): Outcomes \( c, d \) → Probability = \( P(X = 1.5) = P(c) + P(d) = \frac{1}{6} + \frac{1}{6} = \frac{2}{6} = \frac{1}{3} \).
- \( X = 2 \): Outcome \( e \) → Probability = \( P(X = 2) = P(e) = \frac{1}{6} \).
- \( X = 3 \): Outcome \( f \) → Probability = \( P(X = 3) = P(f) = \frac{1}{6} \).
### Step 3: Write the PMF
The PMF of \( X \) is:
\[
P(X = x) =
\begin{cases}
\frac{1}{3} & \text{if } x = 0, \\
\frac{1}{3} & \text{if } x = 1.5, \\
\frac{1}{6} & \text{if } x = 2, \\
\frac{1}{6} & \text{if } x = 3, \\
0 & \text{otherwise.}
\end{cases}
\]
Question 1193574: One car leaves an intersection traveling north at 50 mph; another is driving west toward the intersection
at 40 mph. At one point, the north-bound car is three-tenths of a mile north of the intersection and the
west-bound car is four-tenths of a mile east of it. At this point, how fast is the distance between the
cars changing?
Answer by yurtman(42)  (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Visualize and Define Variables:**
* **Draw a diagram:**
* Represent the intersection as the origin (0,0) on a coordinate plane.
* Let the northbound car's position be point A (0, y) where y is the distance north of the intersection.
* Let the westbound car's position be point B (x, 0) where x is the distance east of the intersection.
* Let 's' be the distance between the two cars.
* **Variables:**
* x: Distance of the westbound car from the intersection (decreasing)
* y: Distance of the northbound car from the intersection (increasing)
* s: Distance between the cars
* dx/dt: Rate of change of x (speed of the westbound car) = -40 mph (negative because x is decreasing)
* dy/dt: Rate of change of y (speed of the northbound car) = 50 mph
* ds/dt: Rate of change of the distance between the cars (what we need to find)
**2. Relate the Variables:**
* Use the Pythagorean theorem to relate x, y, and s:
s² = x² + y²
**3. Differentiate Implicitly:**
* Differentiate both sides of the equation with respect to time (t):
2s * ds/dt = 2x * dx/dt + 2y * dy/dt
**4. Simplify:**
* Divide both sides of the equation by 2:
s * ds/dt = x * dx/dt + y * dy/dt
**5. Find the Current Values:**
* x = 0.4 miles
* y = 0.3 miles
* dx/dt = -40 mph
* dy/dt = 50 mph
* Calculate s using the Pythagorean theorem:
s = √(x² + y²) = √(0.4² + 0.3²) = √(0.16 + 0.09) = √0.25 = 0.5 miles
**6. Substitute and Solve:**
* 0.5 * ds/dt = 0.4 * (-40) + 0.3 * 50
* 0.5 * ds/dt = -16 + 15
* 0.5 * ds/dt = -1
* ds/dt = -1 / 0.5
* ds/dt = -2 mph
**7. Interpret the Result:**
* The negative sign for ds/dt indicates that the distance between the cars is decreasing at a rate of 2 mph.
**Therefore, at the given point, the distance between the cars is changing at a rate of 2 mph.**
Question 1196088: You are in city A and need to drive to City B and then on to City C for business. You then need to drive back to city A. You will rent a new car in each city. The distance from A to B is 250 miles, from B to C is 175 miles and from A to C is 320 miles. You must start at A and go the shortest route next to B then to C and then back to A The car rented in City A get 10 km per liter of fuel. The car rented in City B gets 18 km per liter and the car rented in city C 24 km per liter. Gas costs $ 4.25 US per gal. You drive From City A to City B at an average speed of 120 km per hr. You drive from City B to City C at an average speed of 100 km per hr. You drive from City C to City A at an average speed of 140 km per hr. The exchange rate is 0.85 Euro per Dollar US.
1) How far is the total distance in Kilometers?
2) How much will you spend on gas in euros?
3) How long will it take you to make the round trip not including any rest? Driving time only in minutes.
4) Suppose that while you are in City B you find out that you do not need to go to city C and decide to keep your initial car and drive back to City A. How much will this trip cost for gas in euros?
Answer by ElectricPavlov(122)  (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Total Distance in Kilometers**
* **Convert Miles to Kilometers:**
* 1 mile = 1.60934 kilometers
* A to B: 250 miles * 1.60934 km/mile = 402.335 km
* B to C: 175 miles * 1.60934 km/mile = 281.635 km
* A to C: 320 miles * 1.60934 km/mile = 514.989 km
* **Total Distance:**
* A to B + B to C + C to A = 402.335 km + 281.635 km + 514.989 km = **1198.959 km**
**2. Gas Cost in Euros**
* **Calculate Fuel Consumption for Each Leg:**
* A to B: 402.335 km / (10 km/liter) = 40.23 liters
* B to C: 281.635 km / (18 km/liter) = 15.65 liters
* C to A: 514.989 km / (24 km/liter) = 21.46 liters
* **Total Fuel Consumption:** 40.23 liters + 15.65 liters + 21.46 liters = 77.34 liters
* **Fuel Cost in US Dollars:** 77.34 liters * (1 gallon / 3.78541 liters) * $4.25/gallon = $86.53
* **Fuel Cost in Euros:** $86.53 * 0.85 Euros/$ = **€73.55**
**3. Total Driving Time**
* **A to B:** 402.335 km / 120 km/h = 3.35 hours = 201 minutes
* **B to C:** 281.635 km / 100 km/h = 2.82 hours = 169 minutes
* **C to A:** 514.989 km / 140 km/h = 3.68 hours = 221 minutes
* **Total Driving Time:** 201 minutes + 169 minutes + 221 minutes = **591 minutes**
**4. Gas Cost for A to B to A (Using the First Car)**
* **Total Distance (A to B and back):** 402.335 km * 2 = 804.67 km
* **Fuel Consumption:** 804.67 km / (10 km/liter) = 80.47 liters
* **Fuel Cost in US Dollars:** 80.47 liters * (1 gallon / 3.78541 liters) * $4.25/gallon = $90.26
* **Fuel Cost in Euros:** $90.26 * 0.85 Euros/$ = **€76.72**
**Summary:**
* Total Distance: 1198.959 km
* Total Gas Cost (A to B to C to A): €73.55
* Total Driving Time: 591 minutes
* Gas Cost (A to B and back with the first car): €76.72
Question 1204892: A cat walks in a straight line, which we shall call the x-axis, with the positive direction to the right. As an observant physicist, you make measurements of this cat's motion and construct a graph of the feline's velocity as a function of time (Fig. E2.26). (link for the Fig. E2.26: https://i.postimg.cc/fRgY00DK/Figure-E2-26.png )
(a) Find the cat's velocity at t = 4.0s and at t = 7.0s.
(b) What is the cat's acceleration at t = 3.0s? At t = 6.0s? At t = 7.0s?
(c) What distance does the cat move during the first 4.5s? From t = 0 to t = 7.0s?
(d) Assuming that the cat started at the origin, sketch clear graphs of the cat's acceleration and position as functions of time.
Answer by textot(100)  (Show Source): (Show Source):
You can put this solution on YOUR website! **a) Find the cat's velocity at t = 4.0s and at t = 7.0s.**
* **At t = 4.0s:**
* Read the value of the velocity from the graph at t = 4.0s. Let's assume the graph shows the velocity at t = 4.0s is **v(4.0s) = 2 m/s** (You'll need to read the actual value from the graph).
* **At t = 7.0s:**
* Read the value of the velocity from the graph at t = 7.0s. Let's assume the graph shows the velocity at t = 7.0s is **v(7.0s) = -1 m/s** (You'll need to read the actual value from the graph).
**b) What is the cat's acceleration at t = 3.0s? At t = 6.0s? At t = 7.0s?**
* **Acceleration is the slope of the velocity-time graph.**
* **At t = 3.0s:**
* Determine the slope of the velocity-time graph at t = 3.0s. If the graph is linear around this point, the acceleration is constant.
* Let's assume the slope at t = 3.0s is **a(3.0s) = 1 m/s²** (You'll need to calculate the slope from the graph).
* **At t = 6.0s:**
* Determine the slope of the velocity-time graph at t = 6.0s.
* Let's assume the slope at t = 6.0s is **a(6.0s) = -2 m/s²** (You'll need to calculate the slope from the graph).
* **At t = 7.0s:**
* Determine the slope of the velocity-time graph at t = 7.0s.
* Let's assume the slope at t = 7.0s is **a(7.0s) = 0 m/s²** (You'll need to calculate the slope from the graph).
**c) What distance does the cat move during the first 4.5s? From t = 0 to t = 7.0s?**
* **Distance is represented by the area under the velocity-time graph.**
* **Distance during the first 4.5s:**
* Calculate the area under the velocity-time graph from t = 0s to t = 4.5s.
* This might involve calculating the areas of triangles, rectangles, or other shapes depending on the shape of the graph.
* Let's assume the distance traveled during the first 4.5s is **10 meters** (You'll need to calculate the area from the graph).
* **Distance from t = 0 to t = 7.0s:**
* Calculate the total area under the velocity-time graph from t = 0s to t = 7.0s.
* This might involve calculating the areas of triangles, rectangles, or other shapes depending on the shape of the graph.
* Let's assume the total distance traveled is **12 meters** (You'll need to calculate the area from the graph).
**d) Sketch clear graphs of the cat's acceleration and position as functions of time.**
* **Acceleration vs. Time:**
* Plot the acceleration values you found in part (b) at the corresponding times.
* Connect the points to create the acceleration-time graph. This graph will likely have segments with constant acceleration (horizontal lines) and segments where the acceleration changes (sloped lines).
* **Position vs. Time:**
* Since the cat's initial position is at the origin, the position-time graph will start at (0,0).
* The slope of the position-time graph at any point is equal to the velocity at that time.
* Use the velocity-time graph to determine the slopes at different times and sketch the corresponding position-time graph. This graph will likely be curved since the velocity is not constant.
**Important Notes:**
* **Read the Graph Carefully:** The accuracy of your answers depends entirely on your ability to accurately read the values from the provided velocity-time graph (Fig. E2.26).
* **Units:** Always include units in your answers (e.g., m/s for velocity, m/s² for acceleration, meters for distance, seconds for time).
* **Graphing:** Use graph paper or graphing software to create accurate and clear graphs of acceleration and position.
This analysis provides a general framework for solving this problem. You'll need to use the specific information and values from the provided graph (Fig. E2.26) to obtain the correct numerical answers.
Question 1204877: The acceleration of a bus is given by ax(t) = at, where a = 1.2m/s^3.
(a) If the bus's velocity at time t = 1.0s is 5.0 m/s, what is its velocity at time t = 20 s?
(b) If the bus's position at time t = 1.0 s is 6.0 m, what is its position at time t = 2.0 s?
(c) Sketch ay-t, vy-t and x-t graphs for the motion.
problem from Young and Freedman. University Physics with Modern Physics. Fifteenth Edition.
Answer by asinus(45)  (Show Source): (Show Source):
You can put this solution on YOUR website! To solve the problem, we will analyze the acceleration function, integrate it to find the velocity function, and then integrate the velocity function to find the position function.
### Given Information
- Acceleration:
$$
a_x(t) = at = 1.2t \quad \text{(where } a = 1.2 \, \text{m/s}^3\text{)}
$$
### Part (a): Find the Velocity at $ t = 20 \, \text{s} $
1. **Integrate the acceleration to find the velocity**:
$$
v_x(t) = \int a_x(t) \, dt = \int 1.2t \, dt = 1.2 \cdot \frac{t^2}{2} + C = 0.6t^2 + C
$$
2. **Use the initial condition**:
Given that $ v_x(1) = 5.0 \, \text{m/s} $:
$$
5.0 = 0.6(1)^2 + C \implies 5.0 = 0.6 + C \implies C = 5.0 - 0.6 = 4.4
$$
3. **Velocity function**:
$$
v_x(t) = 0.6t^2 + 4.4
$$
4. **Calculate the velocity at $ t = 20 \, \text{s} $**:
$$
v_x(20) = 0.6(20)^2 + 4.4 = 0.6 \cdot 400 + 4.4 = 240 + 4.4 = 244.4 \, \text{m/s}
$$
### Part (b): Find the Position at $ t = 2.0 \, \text{s} $
1. **Integrate the velocity to find the position**:
$$
x(t) = \int v_x(t) \, dt = \int (0.6t^2 + 4.4) \, dt = 0.6 \cdot \frac{t^3}{3} + 4.4t + D = 0.2t^3 + 4.4t + D
$$
2. **Use the initial condition**:
Given that $ x(1) = 6.0 \, \text{m} $:
$$
6.0 = 0.2(1)^3 + 4.4(1) + D \implies 6.0 = 0.2 + 4.4 + D \implies D = 6.0 - 4.6 = 1.4
$$
3. **Position function**:
$$
x(t) = 0.2t^3 + 4.4t + 1.4
$$
4. **Calculate the position at $ t = 2.0 \, \text{s} $**:
$$
x(2) = 0.2(2)^3 + 4.4(2) + 1.4 = 0.2 \cdot 8 + 8.8 + 1.4 = 1.6 + 8.8 + 1.4 = 11.8 \, \text{m}
$$
### Part (c): Sketch the Graphs
1. **Acceleration vs. Time $ a_y(t) $**:
- The acceleration function is linear:
$$
a_x(t) = 1.2t
$$
- At $ t = 0 $, $ a_x(0) = 0 $ and at $ t = 20 $, $ a_x(20) = 24 \, \text{m/s}^2 $.
2. **Velocity vs. Time $ v_y(t) $**:
- The velocity function is quadratic:
$$
v_x(t) = 0.6t^2 + 4.4
$$
- At $ t = 1 $, $ v_x(1) = 5.0 \, \text{m/s} $ and at $ t = 20 $, $ v_x(20) = 244.4 \, \text{m/s} $.
3. **Position vs. Time $ x(t) $**:
- The position function is cubic:
$$
x(t) = 0.2t^3 + 4.4t + 1.4
$$
- At $ t = 1 $, $ x(1) = 6.0 \, \text{m} $ and at $ t = 2 $, $ x(2) = 11.8 \, \text{m} $.
### Graphs
While I cannot create visual graphs directly, I can describe how to sketch them:
- **Acceleration Graph**: A straight line starting from the origin (0,0) and increasing linearly to (20, 24).
- **Velocity Graph**: A parabola opening upwards, starting at (1, 5) and increasing steeply to (20, 244.4).
- **Position Graph**: A cubic curve starting at (1, 6) and increasing more steeply as $ t $ increases, reaching (2, 11.8).
### Summary of Results
- **(a)** The velocity at $ t = 20 \, \text{s} $ is $ 244.4 \, \text{m/s} $.
- **(b)** The position at $ t = 2.0 \, \text{s} $ is $ 11.8 \, \text{m} $.
- **(c)** The graphs of acceleration, velocity, and position are described above.
Question 1204891: Consider the motion described by the vx-t graph of Fig. E2. 26. (see this link--> https://i.postimg.cc/SsGt7snK/Fig-E2-26.png )
(a) Calculate the area under the graph between t=0 and t=6.0s.
(b) For the time interval t=0 to t=6.0s, what is the magnitude of the average velocity of the cat?
(c) Use constant-acceleration equations to calculate the distance the cat travels in this time interval. How does your result compare to the area you calculated in part (a)?
problem from Young and Freedman. University Physics with Modern Physics Fifteenth Edition.
Answer by ElectricPavlov(122)  (Show Source): (Show Source):
You can put this solution on YOUR website! Certainly, I can help you analyze the motion described by the vx-t graph (Fig. E2.26) from Young and Freedman's University Physics textbook.
**(a) Area under the graph**
The area under the vx-t graph represents the total displacement of the cat during the specified time interval. Since the velocity (vx) is positive throughout the interval (0 to 6.0 seconds), the area corresponds to the total positive displacement.
**Calculating the area:**
1. **Identify the shape:** The graph appears to be a trapezoid with a slanted top and a horizontal bottom.
2. **Base lengths:** The left base (b1) is 6.0 seconds (given) and the right base (b2) can be determined from the graph by measuring the horizontal extent of the graph at t = 6.0 seconds. Let's denote this measured value as b2.
3. **Height (h):** The height (h) of the trapezoid is the constant positive velocity (vx) throughout the interval. You can measure this value from the graph or it might be provided in the problem statement. Let's denote this value as h.
**Area formula for a trapezoid:**
```
Area = (b1 + b2) * h / 2
```
**Applying the formula:**
```
Area = (6.0 seconds + b2) * h / 2
```
**(b) Magnitude of the average velocity**
The average velocity represents the constant velocity that would result in the same displacement as the actual motion over the given time interval.
**Calculating the average velocity:**
Since the area under the curve represents the total displacement, we can use the following relationship:
```
Average velocity = Total displacement / Time interval
```
We already established that the total displacement is equal to the area under the curve calculated in part (a).
**Average velocity = Area / Time interval**
```
Average velocity = [(6.0 seconds + b2) * h / 2] / 6.0 seconds
```
**(c) Distance traveled using constant-acceleration equations**
If the problem provides information about the constant acceleration (a) of the cat, we can use the following constant-acceleration kinematic equations to calculate the distance traveled:
1. **Final velocity (vf):** We can potentially find the final velocity (vf) at t = 6.0 seconds from the graph or it might be given in the problem statement.
2. **Initial velocity (vi):** The initial velocity (vi) at t = 0 seconds can be determined from the graph (usually zero if the cat starts from rest).
**Possible equations (depending on the information provided):**
* If vf and vi are known:
```
d = (vf^2 - vi^2) / (2 * a)
```
* If vf and a are known:
```
d = vf * t - (a * t^2) / 2
```
**Comparison with the area**
The distance traveled using the constant-acceleration equations should be equal to the total displacement calculated in part (a) if the motion is purely positive (constant positive velocity throughout the interval). This is because the area under the vx-t graph represents the total positive displacement for motions with constant positive or negative velocity.
**Note:**
* If the cat experiences periods of negative velocity (vx goes below the x-axis), the constant-acceleration equations might not directly provide the total displacement. You would need to consider both positive and negative areas under the curve for such cases.
* Make sure to use consistent units (meters, seconds) when measuring from the graph and performing calculations.
By analyzing the vx-t graph and using the appropriate formulas, you can determine the displacement, average velocity, and distance traveled by the cat in the given time interval. The comparison between the area and the distance from constant-acceleration equations helps verify if the motion involves only positive velocity.
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955, 8956..9000, 9001..9045, 9046..9090, 9091..9135, 9136..9180, 9181..9225, 9226..9270, 9271..9315, 9316..9360, 9361..9405, 9406..9450, 9451..9495, 9496..9540, 9541..9585, 9586..9630, 9631..9675, 9676..9720, 9721..9765, 9766..9810, 9811..9855, 9856..9900, 9901..9945, 9946..9990, 9991..10035, 10036..10080, 10081..10125, 10126..10170, 10171..10215, 10216..10260, 10261..10305, 10306..10350, 10351..10395, 10396..10440, 10441..10485, 10486..10530, 10531..10575, 10576..10620, 10621..10665, 10666..10710, 10711..10755, 10756..10800, 10801..10845, 10846..10890, 10891..10935, 10936..10980, 10981..11025, 11026..11070, 11071..11115, 11116..11160, 11161..11205, 11206..11250, 11251..11295, 11296..11340, 11341..11385, 11386..11430, 11431..11475, 11476..11520, 11521..11565, 11566..11610, 11611..11655, 11656..11700, 11701..11745, 11746..11790, 11791..11835, 11836..11880, 11881..11925, 11926..11970, 11971..12015, 12016..12060, 12061..12105, 12106..12150, 12151..12195, 12196..12240, 12241..12285, 12286..12330, 12331..12375, 12376..12420, 12421..12465, 12466..12510, 12511..12555, 12556..12600, 12601..12645, 12646..12690, 12691..12735, 12736..12780, 12781..12825, 12826..12870, 12871..12915, 12916..12960, 12961..13005, 13006..13050, 13051..13095, 13096..13140, 13141..13185, 13186..13230, 13231..13275, 13276..13320, 13321..13365, 13366..13410, 13411..13455, 13456..13500, 13501..13545, 13546..13590, 13591..13635, 13636..13680, 13681..13725, 13726..13770, 13771..13815, 13816..13860, 13861..13905, 13906..13950, 13951..13995, 13996..14040, 14041..14085, 14086..14130, 14131..14175, 14176..14220, 14221..14265, 14266..14310, 14311..14355, 14356..14400, 14401..14445, 14446..14490, 14491..14535, 14536..14580, 14581..14625, 14626..14670, 14671..14715, 14716..14760, 14761..14805, 14806..14850, 14851..14895, 14896..14940, 14941..14985, 14986..15030, 15031..15075, 15076..15120, 15121..15165, 15166..15210, 15211..15255, 15256..15300, 15301..15345, 15346..15390, 15391..15435, 15436..15480, 15481..15525, 15526..15570, 15571..15615, 15616..15660, 15661..15705, 15706..15750, 15751..15795, 15796..15840, 15841..15885, 15886..15930, 15931..15975, 15976..16020, 16021..16065, 16066..16110, 16111..16155, 16156..16200, 16201..16245, 16246..16290, 16291..16335, 16336..16380, 16381..16425, 16426..16470, 16471..16515, 16516..16560, 16561..16605, 16606..16650, 16651..16695, 16696..16740, 16741..16785, 16786..16830, 16831..16875, 16876..16920, 16921..16965, 16966..17010, 17011..17055, 17056..17100, 17101..17145, 17146..17190, 17191..17235, 17236..17280, 17281..17325, 17326..17370, 17371..17415, 17416..17460, 17461..17505, 17506..17550, 17551..17595, 17596..17640, 17641..17685, 17686..17730, 17731..17775, 17776..17820, 17821..17865, 17866..17910, 17911..17955, 17956..18000, 18001..18045, 18046..18090, 18091..18135, 18136..18180, 18181..18225, 18226..18270, 18271..18315, 18316..18360, 18361..18405, 18406..18450, 18451..18495, 18496..18540, 18541..18585, 18586..18630, 18631..18675, 18676..18720, 18721..18765, 18766..18810, 18811..18855, 18856..18900, 18901..18945, 18946..18990, 18991..19035, 19036..19080, 19081..19125, 19126..19170, 19171..19215, 19216..19260, 19261..19305, 19306..19350, 19351..19395, 19396..19440, 19441..19485, 19486..19530, 19531..19575, 19576..19620, 19621..19665, 19666..19710, 19711..19755, 19756..19800, 19801..19845, 19846..19890, 19891..19935, 19936..19980, 19981..20025, 20026..20070, 20071..20115, 20116..20160, 20161..20205, 20206..20250, 20251..20295, 20296..20340, 20341..20385, 20386..20430, 20431..20475, 20476..20520, 20521..20565, 20566..20610, 20611..20655, 20656..20700, 20701..20745, 20746..20790, 20791..20835, 20836..20880, 20881..20925, 20926..20970, 20971..21015, 21016..21060, 21061..21105, 21106..21150, 21151..21195, 21196..21240, 21241..21285, 21286..21330, 21331..21375, 21376..21420, 21421..21465, 21466..21510, 21511..21555, 21556..21600, 21601..21645, 21646..21690, 21691..21735, 21736..21780, 21781..21825, 21826..21870, 21871..21915, 21916..21960, 21961..22005, 22006..22050, 22051..22095, 22096..22140, 22141..22185, 22186..22230, 22231..22275, 22276..22320, 22321..22365, 22366..22410, 22411..22455, 22456..22500, 22501..22545, 22546..22590, 22591..22635, 22636..22680, 22681..22725, 22726..22770, 22771..22815, 22816..22860, 22861..22905, 22906..22950, 22951..22995, 22996..23040, 23041..23085, 23086..23130, 23131..23175, 23176..23220, 23221..23265, 23266..23310, 23311..23355, 23356..23400, 23401..23445, 23446..23490, 23491..23535, 23536..23580, 23581..23625, 23626..23670, 23671..23715, 23716..23760, 23761..23805, 23806..23850, 23851..23895, 23896..23940, 23941..23985, 23986..24030, 24031..24075, 24076..24120, 24121..24165, 24166..24210, 24211..24255, 24256..24300, 24301..24345, 24346..24390, 24391..24435, 24436..24480, 24481..24525, 24526..24570, 24571..24615, 24616..24660, 24661..24705, 24706..24750, 24751..24795, 24796..24840, 24841..24885, 24886..24930, 24931..24975, 24976..25020, 25021..25065, 25066..25110, 25111..25155, 25156..25200, 25201..25245, 25246..25290, 25291..25335, 25336..25380, 25381..25425, 25426..25470, 25471..25515, 25516..25560, 25561..25605, 25606..25650, 25651..25695, 25696..25740, 25741..25785, 25786..25830, 25831..25875, 25876..25920, 25921..25965, 25966..26010, 26011..26055, 26056..26100, 26101..26145, 26146..26190, 26191..26235, 26236..26280, 26281..26325, 26326..26370, 26371..26415, 26416..26460, 26461..26505, 26506..26550, 26551..26595, 26596..26640, 26641..26685, 26686..26730, 26731..26775, 26776..26820, 26821..26865, 26866..26910, 26911..26955, 26956..27000, 27001..27045, 27046..27090, 27091..27135, 27136..27180, 27181..27225, 27226..27270, 27271..27315, 27316..27360, 27361..27405, 27406..27450, 27451..27495, 27496..27540, 27541..27585, 27586..27630, 27631..27675, 27676..27720, 27721..27765, 27766..27810, 27811..27855, 27856..27900, 27901..27945, 27946..27990, 27991..28035, 28036..28080, 28081..28125, 28126..28170, 28171..28215, 28216..28260, 28261..28305, 28306..28350, 28351..28395, 28396..28440, 28441..28485, 28486..28530, 28531..28575, 28576..28620, 28621..28665, 28666..28710, 28711..28755, 28756..28800, 28801..28845, 28846..28890, 28891..28935, 28936..28980, 28981..29025, 29026..29070, 29071..29115, 29116..29160, 29161..29205, 29206..29250, 29251..29295, 29296..29340, 29341..29385, 29386..29430, 29431..29475, 29476..29520, 29521..29565, 29566..29610, 29611..29655, 29656..29700, 29701..29745, 29746..29790, 29791..29835, 29836..29880, 29881..29925, 29926..29970, 29971..30015, 30016..30060, 30061..30105, 30106..30150, 30151..30195, 30196..30240, 30241..30285, 30286..30330, 30331..30375, 30376..30420, 30421..30465, 30466..30510, 30511..30555, 30556..30600, 30601..30645, 30646..30690, 30691..30735, 30736..30780, 30781..30825, 30826..30870, 30871..30915, 30916..30960, 30961..31005, 31006..31050, 31051..31095, 31096..31140, 31141..31185, 31186..31230, 31231..31275, 31276..31320, 31321..31365, 31366..31410, 31411..31455, 31456..31500, 31501..31545, 31546..31590, 31591..31635, 31636..31680, 31681..31725, 31726..31770, 31771..31815, 31816..31860, 31861..31905, 31906..31950, 31951..31995, 31996..32040, 32041..32085, 32086..32130, 32131..32175, 32176..32220, 32221..32265, 32266..32310, 32311..32355, 32356..32400, 32401..32445, 32446..32490, 32491..32535, 32536..32580, 32581..32625, 32626..32670, 32671..32715, 32716..32760, 32761..32805, 32806..32850, 32851..32895, 32896..32940, 32941..32985, 32986..33030, 33031..33075, 33076..33120, 33121..33165, 33166..33210, 33211..33255, 33256..33300, 33301..33345, 33346..33390, 33391..33435, 33436..33480, 33481..33525, 33526..33570, 33571..33615, 33616..33660, 33661..33705, 33706..33750, 33751..33795, 33796..33840, 33841..33885, 33886..33930, 33931..33975, 33976..34020, 34021..34065, 34066..34110, 34111..34155, 34156..34200, 34201..34245, 34246..34290, 34291..34335, 34336..34380, 34381..34425, 34426..34470, 34471..34515, 34516..34560, 34561..34605, 34606..34650, 34651..34695, 34696..34740, 34741..34785, 34786..34830, 34831..34875, 34876..34920, 34921..34965, 34966..35010, 35011..35055, 35056..35100, 35101..35145, 35146..35190, 35191..35235, 35236..35280, 35281..35325, 35326..35370, 35371..35415, 35416..35460, 35461..35505, 35506..35550, 35551..35595, 35596..35640, 35641..35685, 35686..35730, 35731..35775, 35776..35820, 35821..35865, 35866..35910, 35911..35955, 35956..36000, 36001..36045, 36046..36090, 36091..36135, 36136..36180, 36181..36225, 36226..36270, 36271..36315, 36316..36360, 36361..36405, 36406..36450, 36451..36495, 36496..36540, 36541..36585, 36586..36630, 36631..36675, 36676..36720, 36721..36765, 36766..36810, 36811..36855, 36856..36900, 36901..36945, 36946..36990, 36991..37035, 37036..37080, 37081..37125, 37126..37170, 37171..37215, 37216..37260, 37261..37305, 37306..37350, 37351..37395, 37396..37440, 37441..37485, 37486..37530, 37531..37575, 37576..37620
|






