Write that system in the matrix form AX = B
First find the inverse of 
:
To do that:
1. Find the value of its determinant, 
2. Swap the upper left and lower right elements of ,
getting
[In this case it didn't change anything since they were both 3, but in
other problems it will be different and you must swap them]
3. Then change the signs of the upper right and lower left elements,
getting 
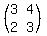4. Divide every element by the value of the determinant of the
original matrix which we found to be 13 in step 1, getting
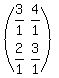or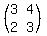
[In this case it didn't change anything since the determinant was 1, but
in other problems it will be different and you must divide.]
This is the inverse A-1 of
the original matrix A.
Left-multiply both sides of the given matrix equation, AX=B
by this inverse, getting the form A-1(AX)=A-1B
Use the associative principle to move the parentheses around
the first two matrices on the left, getting the form (A-1A)X=A-1B
Do the matrix multiplication:
Simplify:
Simplify some more:
This is the form IX=A-1B
Multiply the matrices on the left:
Simplify:
. This is the form X=A-1B.
So the solution is 
and 
Edwin
