Tutors Answer Your Questions about Surface-area (FREE)
Question 1167256: If the area of a circle(A) has an area of a sector of the circle(a),an arc length(I) and circumference(C), deduce a formula for the arc length(I),in terms of the area of the sector and the radius of the circle(r). Hence calculate arc length of the sector of a circle with radius 5cm and area 25cm^2.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! The formula for the arc length ($l$) in terms of the area of the sector ($a$) and the radius of the circle ($r$) is:
$$l = \frac{2a}{r}$$
***
## Deduction of the Formula
This derivation uses the ratio between the sector's properties and the circle's total properties, which are proportional to the central angle ($\theta$).
### 1. Sector Area and Circle Area Relationship
The ratio of the sector's area ($a$) to the total circle's area ($A$) is equal to the ratio of the sector's central angle ($\theta$) to the total angle ($2\pi$ radians):
$$\frac{\text{Sector Area}}{\text{Circle Area}} = \frac{\text{Arc Length}}{\text{Circumference}} = \frac{\text{Sector Angle}}{\text{Full Angle}}$$
Using the area relationship:
$$\frac{a}{A} = \frac{\theta}{2\pi}$$
Since $A = \pi r^2$, we have:
$$\frac{a}{\pi r^2} = \frac{\theta}{2\pi}$$
Solving for the angle $\theta$:
$$\theta = \frac{2\pi a}{\pi r^2} = \frac{2a}{r^2}$$
(Note: This formula gives $\theta$ in radians.)
### 2. Arc Length Formula
The arc length ($l$) is defined by the formula:
$$l = r\theta$$
Substitute the expression for $\theta$ into the arc length formula:
$$l = r \left(\frac{2a}{r^2}\right)$$
Simplify by canceling one $r$:
$$l = \frac{2a}{r}$$
***
## Calculation of Arc Length
Using the deduced formula, we can calculate the arc length with the given values:
* Radius ($r$): $5 \text{ cm}$
* Area of the sector ($a$): $25 \text{ cm}^2$
$$l = \frac{2a}{r}$$
$$l = \frac{2 \times 25 \text{ cm}^2}{5 \text{ cm}}$$
$$l = \frac{50 \text{ cm}^2}{5 \text{ cm}}$$
$$l = 10 \text{ cm}$$
The arc length of the sector is **$10 \text{ cm}$**.
Question 508922: this question is in my saxon algebra 3 book and i cant figure it out
find the surface area of a right circular cone whose slant height is 12 in and whos base has a radius of 5 in
Answer by ikleyn(52915)   (Show Source): (Show Source):
Question 1210245: Evaluate the double integral by converting it into polar coordinates: integral from 1 to 2 integral from 0 to sqrt (2x - x^2) (x^2y + y^3) dy dx
I can get the answer using rectangular coords as 47/60, but conversion into polar and evaluation gets me the wrong answer. I can't seem to get the correct limits or whatever.
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I repeat this my post here for greater reliability.
In January, February, March and April of 2025, @CPhill (which is the synonym of the Google AI)
posted 1941 solved problems to this forum.
He posted them at the rate of 25-30 solved problems per day.
Some of them (many of them) were solved incorrectly.
During these months, I tried to check the incoming problems, but, surely, been a human, not a
computer tool, I was not able to check all of them at the same rate.
Therefore, starting from the end of April 2025, and during May and June 2025, I checked
the remaining problems- those of them where I was competent to check.
I did not check the advanced Statistics problems, since I am not an expert in this field.
I also did not check advanced Finance problems, where I am not an expert.
But I checked a lot of other problems.
So, this file below contains the list of problems that (in my opinion) are solved incorrectly by @CPhill.
So far, this list contains 151 incorrectly solved problems.
For most of them, I placed my correct solutions.
Now some statistical counts.
As I said, the full number of solutions posted by @CPhill was 1941.
Of them, a huge portion were advanced statistics problems, which I did not check.
Their number was 2/3 or 3/4 of all problems - I did not count them.
Also, I did not check advanced Finance problems.
I think (I estimate approximately) that I checked from 500 to 600 problems,
As I said, the number of incorrect solutions is 151, so far.
This number 151 does not cover all erroneous solutions by @CPhill - the number
of his erroneous solutions is more: I could miss some of them.
But this ratio "wrong to checked" = "151 to 500 or to 600" is HUGE.
It characterizes the level of this modern/contemporary version of this AI.
********************************************
Surely, it is unacceptable level for an AI.
********************************************
I am not an enemy to AI. But I want we all have right/correct understanding of what is the AI now
in solving school Math problems.
So, I hope that this my huge work on checking this AI is useful both for visitors of this site,
as well as for the developers of this AI.
Probably, in the future I will return to this checking, and then this list of erroneously solved problems will become greater.
ikleyn
June 29, 2025
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
The list of problems solved incorrectly by @CPhill
=====================================================
1208643
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1208643.html
We call a number cozy if every digit in the number is either a $3$ or next to a $3.$ For example, the numbers $333,$ $83,$ $303,$ and $3773$ are all cozy,
but the numbers $32423,$ $786,$ $340,$ and $3999$ are not cozy.
How many positive $10$-digit numbers are cozy?
1209502
https://www.algebra.com/algebra/homework/complex/Complex_Numbers.faq.question.1209502.html
Let be three positive numbers such that:
x^2 + y^2 + z^2 = 2(xy + xz + yz).
x + y + z + \frac{1}{xyz} > 4.
1209450
https://www.algebra.com/algebra/homework/complex/Complex_Numbers.faq.question.1209450.html
A triangle ABC, where |AB| = |AC|, a line CD is drawn from angle C and intersects side AB at D, such that |AD| = |CD| = |BC|.
Find the measure of angle A in degrees.
1193410
https://www.algebra.com/algebra/homework/playground/test.faq.question.1193410.html
Julita owes Jose the following am
a. 55,000 at the end of 4 years,
b. 48,000 at the end of 5 years, and
c. 75,000 due in 3 years from today at 9% converted quarterly.
What single payment at the end of 2 years will settle Julita’s
obligations if money is worth 15% converted monthly?
1193440
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1193440.html
A shipment of 10 items has two defective and eight non defective units. In the inspection of the shipment , a sample of units will be selected and tested.
If a defective unit is found , the shipment of 10 units will be rejected.
If a sample of four is selected , what is the probability that the shipment will be rejected?
1192630
https://www.algebra.com/algebra/homework/playground/lessons/test.faq.question.1192630.html
the semiannual withdrawals possible over 4.5 years from an account earning 5.25% compounded semiannually
and starting with $11,000. (Round your answer to the nearest cent.)
1192634
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1192634.html
In the movie Forrest Gump, the public school required an IQ of at least 80 for admittance.
IQ test scores are normally distributed with mean 100 and standard deviation 16
a. What percentage of people would qualify for admittance to the school.
b. If the public school wishes 95 percent of all children to qualify for admittance,
what minimum IQ test score should be required for admittance?
1209484
https://www.algebra.com/algebra/homework/Surface-area/Surface-area.faq.question.1209484.html
Trapezoid ABCD has diagonals that cross at E. The area of triangle EDC is n².
If AB has length m and DC has length n, find the area of trapezoid ABCD in terms of m and n.
Diagram: https://ibb.co/svwxc0w
1192431
https://www.algebra.com/algebra/homework/coordinate/word/Linear_Equations_And_Systems_Word_Problems.faq.question.1192431.html
you are given 20 true false questions and required to find probability of almost 4 are correct?
1192508 (10)
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1192508.html
A breathalyser test is used by police in an area to determine whether a driver has an excess of alcohol in their blood.
The device is not totally reliable: 7 % of drivers who have not consumed an excess of alcohol give a reading from the breathalyser
as being above the legal limit, while 10 % of drivers who are above the legal limit will give a reading below that level.
Suppose that in fact 14 % of drivers are above the legal alcohol limit, and the police stop a driver at random.
Give answers to the following to four decimal places.
Part a)
What is the probability that the driver is incorrectly classified as being over the limit?
Part b)
What is the probability that the driver is correctly classified as being over the limit?
Part c)
Find the probability that the driver gives a breathalyser test reading that is over the limit.
Part d)
Find the probability that the driver is under the legal limit, given the breathalyser reading is also below the limit.
1192522
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1192522.html
It is estimated that approximately 8.37% Americans are afflicted with diabetes. Suppose that a certain diagnostic evaluation for diabetes
will correctly diagnose 98% of all adults over 40 with diabetes as having the disease and incorrectly diagnoses 3% of all adults over 40
without diabetes as having the disease.
a) Find the probability that a randomly selected adult over 40 does not have diabetes, and is diagnosed as having diabetes
(such diagnoses are called "false positives").
b) Find the probability that a randomly selected adult of 40 is diagnosed as not having diabetes.
c) Find the probability that a randomly selected adult over 40 actually has diabetes, given that he/she is diagnosed as not having diabetes
(such diagnoses are called "false negatives").
(Note: it will be helpful to first draw an appropriate tree diagram modeling the situation)
1209504
https://www.algebra.com/algebra/homework/word/misc/Miscellaneous_Word_Problems.faq.question.1209504.html
Jamie spent 3/4 of her money on 3 books of the same price. Grace spent 5/9 of her money on 2 diaries.
They were each left with an equal amount of money. One book cost $3.30 more than one diary.
How much money did they have altogether.
1192298
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1192298.html
Find the number of permutations of 10 numbers in a spinner.
1192052
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1192052.html
Triplets Peter, Reeta and Nikita have two ways for getting home from school each day: cycle on a tandem bike or walk.
The bike can carry either one or two riders at a time. Regardless of the number of people pedalling, cycling speed
is 5 times walking speed. The triplets always leave school at the same time and always use the same path between school
and home, whether walking or cycling. The school is 5 km from home and their walking speed is 4 kilometres per hour.
a) On Monday, Nikita and Peter cycle and Reeta walks. On reaching the point four-fifths of the way home the bike gets a puncture,
so Nikita and Peter walk the rest of the way home. How far from school is Peeta when the cyclists arrive home?
b) On Tuesday, Peter and Reeta ride the bike and Nikita walks. When the cyclists arrive home, Peter hops off the bike and Reeta rides back
towards school to collect Nikita. How far from school is Nikita when Reeta reaches her?
c) On Wednesday, Reeta and Nikita take the bike and Peter walks. When the cyclists are halfway home, Reeta hops off and walks the rest of the way,
while Nikita heads back to pick up Peter. How far from school is Reeta when her siblings pass her on the bike?
d) On Thursday, it is Reeta's turn to walk. Peter drops Nikita off at a certain point leaving her to walk home. Meanwhile he returns to pick up Reeta
and they cycle home together. If all three arrive home at the same time, how far from school are the drop-off and pick-up points?
Part (d) is interpreted and solved INCORRECTLY by @CPhill.
1209514
https://www.algebra.com/algebra/homework/word/misc/Miscellaneous_Word_Problems.faq.question.1209514.html
There were 220 chickens, ducks and goats on a farm. The ratio of chickens to ducks and goats is 3 to 2. The ratio of goats to ducks and chickens
is 1 to 3. What is the ratio of chickens to ducks to goats. If a goat is sold at $98 each, Find the amount if all the goats are sold.
1209515
https://www.algebra.com/algebra/homework/word/misc/Miscellaneous_Word_Problems.faq.question.1209515.html
There were some oranges in baskets A B and C. The ratio of A to B and C is 1 to 4.
The ratio of C to A and B is 3 to 4.
How many oranges were in C if there were 54 more oranges in B than in A.
1209520
https://www.algebra.com/algebra/homework/Polygons/Polygons.faq.question.1209520.html
Square SQUR has sides of length x. If triangle SQE is equilateral, find the area of triangle QAU.
Link to diagram: https://ibb.co/C58rZ09R
1192249
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1192249.html
Hotel A and B offers 2 types of packages that include lodging only or lodging with
breakfast. From a group of 300 tourists, 30 tourist choose Hotel A for lodging only
and 120 tourists choose Hotel B for lodging with breakfast.
Altogether 110 tourists choose to stay in Hotel A.
A tourist is selected randomly.
(a) What is the probability that the tourist chooses Hotel A or tourists chooses lodging only?
(b) What is the probability that the tourist to choose Hotel B for lodging with breakfast, if he chose Hotel B?
(c) What is the probability that the tourist to choose Hotel A, if he chose lodging without breakfast?
(d) What is the probability that the tourist chose Hotel A without breakfast or choose Hotel B with breakfast?
1192250
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1192250.html
Hotel A and B offers 2 types of packages that include lodging only or lodging with
breakfast. From a group of 300 tourists, 30 tourist choose Hotel A for lodging only
and 120 tourists choose Hotel B for lodging with breakfast.
Altogether 110 tourists choose to stay in Hotel A.
A tourist is selected randomly.
(a) What is the probability that the tourist chooses Hotel A or tourists chooses lodging only?
(b) What is the probability that the tourist to choose Hotel B for lodging with breakfast, if he chose Hotel B?
(c) What is the probability that the tourist to choose Hotel A, if he chose lodging without breakfast?
(d) What is the probability that the tourist chose Hotel A without breakfast or choose Hotel B with breakfast?
1209524 (20)
https://www.algebra.com/algebra/homework/Circles/Circles.faq.question.1209524.html
Sector ABC is 1/12 of a circle with diameter 24k. Line segment AD is perpendicular to segment BC.
Find the area of the shaded region.
Link to diagram: https://ibb.co/5gNwX0K6
1191371
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1191371.html
Suppose you want to have $600,000 for retirement in 30 years. Your account earns 10% interest.
How much would you need to deposit in the account each month?
1190652
https://www.algebra.com/algebra/homework/word/finance/Money_Word_Problems.faq.question.1190654.html
What is the present value of an ordinary annuity having semi-annual payments
of 8, 000 pesos for 12 years with an interest rate of 12% compounded annually?
1209532
https://www.algebra.com/algebra/homework/Circles/Circles.faq.question.1209532.html
Point R is chosen on the circumference of a circle and arc PQ is drawn with R as its center.
If P and Q are joined, the line segment formed is a diameter of the circle with length 2r cm.
Find the area of the shaded region in terms of r, in square centimeters.
Link to diagram: https://ibb.co/GQFdy2SV
1186907
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1186907.html
The world production of gold from 1970 to 1990 can be modelled by G = 5.2t 2 - 76t + 1492, where G is the
number of tonnes of gold and t is the number of years since 1970, t = 1 for 1971 and so on.
a. What was the most amount of gold mined in one year?
b. How much gold was mined in 1978?
1186928
https://www.algebra.com/algebra/homework/word/misc/Miscellaneous_Word_Problems.faq.question.1186928.html
For each of the following statements, explain why it is true for all functions f and g or give
an example of specific functions f and g showing that it is false.
a. All elements in the domain of g must be in the domain of f o g (fog)
b. All elements in the range of f must be in the range of f o g
1187156
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1187156.html
During the scholarship examination of a certain scholarship grant taken by 10,000 applicants,
Donnabelle's score was 350 greater than the scores of 8995 applicants who took the examination.
What is the percentile of Donnabelle's score?
1209553
https://www.algebra.com/algebra/homework/playground/test.faq.question.1209553.html
If x + (24)^(⅓) = (16)^(⅓) + (36)^(⅓)
find (10³/x⁶) - (x³/10³) - (30/x³)
1186854
https://www.algebra.com/algebra/homework/Length-and-distance/Length-and-distance.faq.question.1186854.html
Two vertices of a regular quadrilateral are A(0,4) and B(0,24). Which of the following could be the other two vertices?
a. C(4,4) and D(4,24)
b. C(24,4) and D(24,24)
c. C(8,24) and D(8,4)
d. C(0,8) and D(0,28)
1186205
https://www.algebra.com/algebra/college/linear/Linear_Algebra.faq.question.1186205.html
The Intellectual Company produces a chemical solution used for cleaning carpets.
This chemical is made from a mixture of two other chemicals which contain cleaning agent X and cleaning agent Y.
Their product must contain 175 units of agent X and 150 units of agent Y and weigh at least 100 pounds.
Chemical A costs ₱ 8 per pound, while chemical B costs ₱ 6 per pound.
Chemical A contains one unit of agent X and three units of agent Y.
Chemical B contains seven units of agent X and one unit of agent Y.
a. Set up the following:
i. Variables
ii. Constraints
iii. Objective Function
b. Find the minimum cost
c. Determine the best combination of the ingredients to minimize the cost.
1186248 (30)
https://www.algebra.com/algebra/college/linear/Linear_Algebra.faq.question.1186248.html
The Intellectual Company produces a chemical solution used for cleaning carpets.
This chemical is made from a mixture of two other chemicals which contain cleaning agent X and cleaning agent Y.
Their product must contain 175 units of agent X and 150 units of agent Y and weigh at least 100 pounds.
Chemical A costs ₱ 8 per pound, while chemical B costs ₱ 6 per pound.
Chemical A contains one unit of agent X and three units of agent Y.
Chemical B contains seven units of agent X and one unit of agent Y.
a. Set up the following:
i. Variables
ii. Constraints
iii. Objective Function
b. Find the minimum cost
c. Determine the best combination of the ingredients to minimize the cost.
1186455
https://www.algebra.com/algebra/homework/word/finance/Money_Word_Problems.faq.question.1186455.amp
On her recent birthday, April 22, 2001, Nicole was given by her mother a certain sum of money as birthday present.
She decided to invest the said amount on 20% exact simple interest. If the account will mature
on Christmas day at an amount of P 10,000.00, How much did Nicole receive from her mother on her birthday
1186235
beginning at the origin a spiral is constructed from three semmi-circles with centres at (1,0), (0,0) and (2,0)
the area of the shaded region in u^2 is?
https://drive.google.com/file/d/1OLUZW44XSyKqEXVuIhuwpkMDvT8E14xU/view?usp=sharing
1186272
https://www.algebra.com/algebra/homework/Length-and-distance/Length-and-distance.faq.question.1186272.html
On a wall, 60 1/2 cm wide, Oscar is going to hang three pictures beside each other, each measuring 9 1/3 cm wide.
He will leave 3 1/2 cm in between each pair of adjacent pictures. He plans to use two nails to hang each picture,
and will centre these nails leaving 4 cm between each pair. How far, in cm, from the end of the wall(on either side)
will the first nail be placed?
1209558 <<<---=== solution for (a) is incorrect. solution for (c) is incorrect.
https://www.algebra.com/algebra/homework/playground/test.faq.question.1209558.html
a) If 7^sin²x - 7^cos²x = 8
find the value of x.
b) Let m be a given real number, Find all complex numbers x such that,
([x/(x+1)]² + [x/(x-1)]² = m² + m
c) ab = ½, bc = ⅓, ac = 1/6,
find (1/a²) + (1/b²) + (1/c²)
d) 2^x - 3^y = 5
2^(x+2) + 3^(y+2) = 59.
find xy
e) find m,
9^4^m = 4^9^m
f) (7^log₈x)×(x^log₉x) = 3969,
find x.
1186068
Suppose events A and B are independent and
P(A) = 1/4
P(B) = 1/5
Find the probability. (Enter the probability as a fraction.)
_____
P(A ∩ B) the line is above a and b only
1186121
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1186121.html
Tickets for a raffle cost $12. There were 713 tickets sold. One ticket will be randomly selected as the winner,
and that person wins $1800 and also the person is given back the cost of the ticket.
For someone who buys a ticket, what is the Expected Value (the mean of the distribution)?
1185780
https://www.algebra.com/algebra/homework/Graphs/Graphs.faq.question.1185780.html
The director of MIS Center At a large company wants to do stuff consulting station with two shifting teams:
Team A will compromise of 3 senior programmers and 3 system analyst and
team B will consist 2 senior programmers and 5 system analysts.
the director wants to use no more than 42 individuals.
There will be at least 48 hours to be filed during the week, with team A serving for 4 hours and the team B shift servings for 3 hours.
The cost of team A is 3200 per hour and 2800 per hour for team B shift.
Determine the number of shifts each team has to render in order to minimize the cost.
•What is the Test ratio for table 2?
•What is the pivotal/al column in Tableu 1?
•What is the result in the last row of Tableu 4?
•Show the proper representation of Tableu
1209595
https://www.algebra.com/algebra/homework/complex/Complex_Numbers.faq.question.1209595.html
limit x (1 - 2 cos ((pi x)/(3 x - sqrt3))) as x \[LongRightArrow] + \[Infinity]
1209654
https://www.algebra.com/algebra/homework/Systems-of-equations/Systems-of-equations.faq.question.1209654.html
Find the unique pair of real numbers (x,y) satisfying
(6x^2 - 18x + 17) + (3y^2 + 6y + 11) = 28
and x + y = 20.
1209644 (40)
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209644.html
Find all complex solutions to the equation z^8 + 144 = 25z^4 + 10z^6 + 10z^2.
1209645
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209645.html
Find all complex solutions to the equation z^8 + 16 = 17z^4 - 8z^6 - 8z^2.
1209660 <<<---=== the problem is posed incorrectly, and the answer by @CPhill is incorrect
https://www.algebra.com/algebra/homework/Quadratic-relations-and-conic-sections/Quadratic-relations-and-conic-sections.faq.question.1209660.html
Find the conic section represented by the equation
x^2 - 4x + y^2 = y^2 + 8x + 20
1209701
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209701.html
Find a monic quartic polynomial f(x) with rational coefficients whose roots include x = 2 - i \sqrt[3]{3}$.
Give your answer in expanded form.
1209688 <<<---=== Fake problem and wrong solution/answer by @CPhill
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209688.html
The polynomial
f(x) = x^3 + 10x^2 + 21x + 10 + 4x^3 - 17x^2 + 8x - 66
has one integer root. What is it?
1184157
https://www.algebra.com/algebra/homework/Distributive-associative-commutative-properties/Distributive-associative-commutative-properties.faq.question.1184157.html
Construct two examples of bijective function from ZxZ to Q where Z is set of all integers and Q is set
of rational numbers.
1184450
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1184450.html
A certain class has 11 students, 2 of whom are sisters. The class needs to be split across three rooms
for a socially distanced exam, where room A can seat 2 students, room B 3 students, and room C 6 students.
How many ways can the students be divided across the rooms, if the 2 sisters are not allowed to be in
the same room (say, for academic integrity) ?
1184115
https://www.algebra.com/algebra/homework/Percentage-and-ratio-word-problems/Percentage-and-ratio-word-problems.faq.question.1184115.html
Berlin and Cheryl had a total of 6750 stamps. At first, Andy have 50%
of his stamps to Berlin. Berlin then gave 1/3 of her stamps to Cheryl.
Finally, Cheryl gave 1/6 of her stamps to Andy. In the end, the ratio of the
number of Andy’s stamps to the number of Berlin’s stamps became 4:5.
Cheryl had twice the total number of stamps that Andy and Berlin had.
How many stamps did Berlin and Cheryl have in total at first?
1174471
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1174471.html
To save for retirement, Karla Harby put $500 each month into an ordinary annuity for 10 years.
Interest was compounded monthly. At the end of the 10 years, the annuity was worth $84,608.
What annual interest rate did she receive?
The interest rate she received was approximately ___%
1174826
https://www.algebra.com/algebra/homework/Quadratic-relations-and-conic-sections/Quadratic-relations-and-conic-sections.faq.question.1174826.html
find the equation of parabola which has contact of third order with the conic ax^2 +2hxy + by^2 +2gx +2fy +c =0 at origin.
1209808 (50)
https://www.algebra.com/algebra/homework/playground/test.faq.question.1209808.html
Find the value of θ,
sin(20°)*sin(θ) + sin(100°)*sin(20 - θ)° = 0
1209677
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209677.html
When g(x) is divided by x^2 - x - 6, the remainder is 2x + 7. What is the value
of g(8)?
1209710
https://www.algebra.com/algebra/homework/playground/lessons/test.faq.question.1209710.html
4^(1/√x) + 16^(1/√x) = 64^(1/√x)
1209712
https://www.algebra.com/algebra/homework/playground/test.faq.question.1209712.html
If (x√x)^(1/x) = 2, find x.
1181712
https://www.algebra.com/algebra/homework/quadratic/Quadratic_Equations.faq.question.1181712.html
A rocket is being launched vertically over a point 𝐴 on the ground with
a velocity of 550 𝑚𝑖Τℎ𝑟. Twenty five miles away from point 𝐴 on the
ground, there is a photographer video-taping the launch. At what rate
is the angle of elevation of the camera changing when the rocket
achieves an altitude of 25 miles?
1181729
https://www.algebra.com/algebra/homework/Volume/Volume.faq.question.1181729.html
The diameter of a sphere coincides with the axis of a right circular cone, and the surface of the cone intersects the surface of the sphere in in a great circle. Find
(a) the vertical angle of the cone:
(b) the volume of the cone;
(c) the volume common to the two solids:
(d) the volume of that portion of the cone which lies outside the sphere:
(e) the volume of that portion of the sphere which lies outside the cone. Denote radius of sphere by R.
Solve Problem if (a) R=2: (b) R=3.72.
1181730
https://www.algebra.com/algebra/homework/Volume/Volume.faq.question.1181730.html
The center of each of three spheres of radius R lies in the surfaces of the other two.
Pass a plane containing the centers of the spheres.
Find the area common to the three great circles cut from the spheres by this plane.
1181731
https://www.algebra.com/algebra/homework/Volume/Volume.faq.question.1181731.html
A sphere is inscribed in a right circular cone of altitude h and radius of base r.
Write a formula in terms of r and h for the volume of the sphere.
1181618
https://www.algebra.com/algebra/homework/word/travel/Travel_Word_Problems.faq.question.1181618.html
Modern oil tankers weigh more than a 1/2 million tons and have lengths up to one - fourth mile. Such massive ships require a distance of 5.0 km about (3.0 mi)
and a time of 20 minutes to come to a stop from top speed of 30 km/h.what is the magnitude of such ship's average acceleration in m/s squared in coming to a stop?
B. What is the magnitude of the ship's average velocity in m/s
1209741
https://www.algebra.com/algebra/homework/playground/test.faq.question.1209741.html
If 1/9^(1/x) + 1/3^(1/x) = 30,
find x.
1209729 (60)
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209729.html
Let t be a root of f(x) = x^3 - x + 3. Evaluate t^6 - 4t^5 + 7t^4 - 3t^2 + 10t - 13.
1209740
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209740.html
Factor x^2 - 2x - y^2 + 2yz + 5z^2 as the product of two polynomials of degree 1.
1209728
Let r, s, and t be solutions of the equation 3x^3 - 4x^2 - 2x + 12 = 0.
Compute (rs)/t^2 + (rt)/s^2 + (st)/r^2.
1209735
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1209735.html
69% of all Americans are home owners. If 37 Americans are randomly selected, find the probability that
a. Exactly 27 of them are are home owners.
b. At most 27 of them are are home owners.
c. At least 23 of them are home owners.
d. Between 23 and 28 (including 23 and 28) of them are home owners.
1209737
https://www.algebra.com/algebra/homework/word/misc/Miscellaneous_Word_Problems.faq.question.1209737.html
The dots on the opposite faces of a die have a sum of 7.
How many different sum of dots on three adjacent faces are there on a die?
1209731
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209731.html
Let r, s, and t be solutions of the equation x^3 + 2x^2 - 5x + 15 = 0. Compute
1/(r - 2s - 2t) + 1/(s - 2r - 2t) + 1/(t - 2r - 2s)
1180634
https://www.algebra.com/algebra/homework/equations/Equations.faq.question.1180634.html
This pandemic, Abheedette learned to bake while on home quarantine.
She also realized that she will be able to make P60.00 profit per tray of banana muffins
and P120.00 profit per tray of blueberry muffins.
She needs 2 cups of milk and 3 cups of flour to bake a tray of banana muffins.
And, baking a tray of blueberry muffins takes 4 cups of milk and 3 cups of flour.
She has 16 cups of milk and 15 cups of flour.
How many trays of each flavor must be baked to maximize the profit?
a. Define the variable used:
b. LP Model:
c. Identify the feasible region:
d. Corner Points and the objective functions:
e. Optimal Solution (final answer):
1209745
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209745.html
in the blanks, to complete the factorization:
(a^2 + b^2 - c^2)^2 - 4a^2 b^2 - 4a^2 c^2 + 4b^2 c^2 = (a + ___)(a + ___)(a + ___)(a + ___)
1180382
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1180382.html
a particle jumps between three positions A, B, and C. If it starts at A, it stays at A with probability 44%,
and it goes to B with probability 18% and to C with probability 26%. If, however, it starts at C, it goes to A with probability 51%
and to B with probability 16%.
Find the transition matrix.
If the particle stays at A, what is the probability that it stays at A after three jumps?
1179711
Determine the periodic payments on the given loan or mortgage.
$5,000,000 borrowed at 7% for 30 years, with quarterly payments
1179768 (70)
The problem on pendulum
https://gyazo.com/78c37f667cf2af63efadea4314e5642c
1179791
https://www.algebra.com/algebra/homework/Functions/Functions.faq.question.1179791.html
If the area (in square units) of the region under the curve of the function f(x) = 3x − 1 on t he interval [a, 4],
where a < 4, is 12 square units, identify all the possible values of a.
what values are correct?
a. -3
b. 0
c. -16/5
d. 8/3
e. -2
f. 7/2
1179819
https://www.algebra.com/algebra/homework/Sequences-and-series/Sequences-and-series.faq.question.1179819.html
Find the present values of the following annuities
i. RM6,000 every year for 8 years at 12% compounded annually
ii. RM800 every month for 2 years 5 months at 5% compounded monthly.
1179653 - about a pendulum, horizontal displacement.
https://gyazo.com/848645a235363970dae8196a58a2bbdc
1179602
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1179602.html
If 35% of the people in a community use the emergency room at a hospital one year.
Find these probabilities for a sample of 12 people
A) exactly 4 used the emergency room
B) At most 4 used the emergency room
C) At least 10 used the emergency room
1209768 <<<---=== incomplete solution: one solution is found; other solution is missed
https://www.algebra.com/algebra/homework/playground/lessons/test.faq.question.1209768.html
If a = sin50(1 + 2cos170°),
b = sin170°(1 + 2cos140°),
c = sin140°(1 + 2cos50°),
then (3 - 2A)ˣ = (x + 1)²,
find x
1209770 <<<---=== Total, global and fatal deceiving of a reader
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209770.html
Find all (real or nonreal) x satisfying
(x - 3)^4 + (x - 5)^4 = -8 + 6(x - 3)(x - 5)^3 - 11(x - 3)^3 (x - 5).
1179081 <<<---=== The problem is non-sensical. The solution by @CPhill is non-sensical, too.
https://www.algebra.com/algebra/homework/word/finance/Money_Word_Problems.faq.question.1179081.html
Nick has been depositing $190 in a savings account every three months for the past three years. This account paid 3 % convertible quarterly.
Nick has just made the last deposit. Nick is buying a car for $ 14000. He is taking out a car loan. He will use the accumulated value of his savings account
as the downpayment on the car. The loan is at 3 % convertible semiannually and has a term of 4 years. Find the size of Nick's monthly car loan payment.
1209773
https://www.algebra.com/algebra/homework/coordinate/Linear-systems.faq.question.1209773.html
If a_1, a_2, ..., a_19 satisfy
a_1 + a_2 + a_3 + a_4 = 1,
a_2 + a_3 + a_4 + a_5 = 2,
a_3 + a_4 + a_5 + a_6 = 3,
...
a_{16} + a_{17} + a_{18} + a_{19} = 16,
a_{17} + a_{18} + a_{19} + a_1 = 17,
a_{18} + a_{19} + a_1 + a_2 = 18,
a_{19} + a_1 + a_2 + a_3 = 19,
what is the value of a_19?
1178715
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1178715.html
Solve each problem.
1. Your monthly electric bill has a mean of ₱120.00. what is the percentage that you will pay an amount between ₱1,380 and ₱1,740?
2. Suppose the scores in the mathematics exam are normally distributed. If the exam has a mean score of 25 and a standard deviation of 5,what is the probability that if you take th
1178377 (80)
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1178377.html
Woofer Pet Foods produces a low-calorie dog food for overweight dogs. This product is made from beef products and grain. Each pound of beef costs $0.90,
and each pound of grain costs $0.60. A pound of the dog food must contain at least 9 units of Vitamin 1 and 10 units of Vitamin 2.
A pound of beef contains 10 units of Vitamin 1 and 12 units of Vitamin 2.
A pound of grain contains 6 units of Vitamin 1 and 9 units of Vitamin 2.
Formulate this as an LP problem to minimize the cost of the dog food. How many
pounds of beef and grain should be included in each pound of dog food? What is the cost and vitamin content of the final product?
1209775 <<<---=== AI produced the same wrong solution, kind of gibberish, and I reported to AI
https://www.algebra.com/algebra/homework/Systems-of-equations/Systems-of-equations.faq.question.1209775.html
Let a, b, c, and d be distinct real numbers such that
a = sqrt(4 + sqrt(5 + a)),
b = sqrt(4 - sqrt(7 + b)),
c = sqrt(4 + sqrt(9 - c)),
d = sqrt(4 - sqrt(11 - d)).
Compute abcd.
1209776 <<<---=== the "solution" by @CPhill is unreadable gibberish
https://www.algebra.com/algebra/homework/Systems-of-equations/Systems-of-equations.faq.question.1209776.html
Suppose the real numbers $a$, $b$, $x$, and $y$ satisfy the equations
ax + by = 3,
ax^2 + by^2 = 5,
ax^3 + by^3 = 17,
ax^4 + by^4 = 23.
Evaluate ax^5 + by^5.
See the solution at AoPS under this link
https://artofproblemsolving.com/wiki/index.php/1990_AIME_Problems/Problem_15?srsltid=AfmBOoq3eeok8NtsAuOBNtICcVv9fxgXqq0z4Tix5v0NoDfFL11W2Z72
1209790
https://www.algebra.com/algebra/homework/playground/test.faq.question.1209790.html
If x^x = 5, find x^x^(x+1).
1177476 <<<---=== part (a) was solved INCORRECTLY by @CPhill
https://www.algebra.com/algebra/homework/playground/test.faq.question.1177476.html
There are 150 people at an International Medical Conference.
40 are Africans, 70 are women and 110 are doctors.
12 of the women are Africans, 46 of the doctors are women and 31 of the Africans are doctors.
If 5 of the African men are not doctors:
(a) how many of the African women are doctors ?
(b) how many of the men are neither African nor doctors?
1177187
https://www.algebra.com/algebra/homework/Trigonometry-basics/Trigonometry-basics.faq.question.1177187.html
Owen is jumping on a trampoline. When his feet hit the deck of the trampoline, the material depresses
to a minimum height of 2cm. On average, Owen is reaching a maximum height of 200cm every 10 seconds.
Determine the equation of a sinusoidal function that would model this situation, assuming
Owen reaches his first maximum at 6 seconds.
1176885
https://www.algebra.com/algebra/homework/Graphs/Graphs.faq.question.1176885.html
If a simple, connected, graph has 20 vertices, what is the maximum number of edges it can have?
(Recall that a simple graph does not have loops and does not have multiple / parallel edges)
1176989
https://www.algebra.com/algebra/homework/Length-and-distance/Length-and-distance.faq.question.1176989.html
EVOL is a cyclic quadrilateral, inscribed in a circle with center S. Given that the radius of this circle
is 25 in. and angle VEL is 55 degrees, explain your work to find the following measurements.
a) Length of Major Arc VL
b) Angle measure of Minor Arc VL
c) Angle VOL
d) Length of Chord VL
1177001
https://www.algebra.com/algebra/homework/Circles/Circles.faq.question.1177001.html
EVOL is a cyclic quadrilateral, inscribed in a circle with center S. Given that the radius of this circle
is 25 in. and angle VEL is 55 degrees, explain your work to find the following measurements.
a) Length of Major Arc VL
b) Angle measure of Minor Arc VL
c) Angle VOL
d) Length of Chord VL
1176067 <<<---=== Inaccurate/icorrect calculations
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1176067.html
state lotto has a prize that pays $1,700 each week for 40 years.
Find the total value of the prize.
If the state can earn 3% interest on investments, how much money will they need to put
into an account now to cover the weekly prize payments?
1209804 (90)
https://www.algebra.com/algebra/homework/playground/test.faq.question.1209804.html
If sinx + sin²x + sin³x = 1,
find cos⁶x - 4cos⁴x + 8cos²x
1176479
https://www.algebra.com/algebra/homework/Circles/Circles.faq.question.1176479.html
Given seven equal circles on a hexagonal grid, how many permutations are possible where circles are always adjacent
(repetitions such as inversions and reflections excluded)?
1209808
https://www.algebra.com/algebra/homework/playground/test.faq.question.1209808.html
Find the value of θ,
sin(20°)*sin(θ) + sin(100°*sin(20 - θ)° = 0
1209794
(x+4)^2/9+(y+3)^2 /4 =1
1177711
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1177711.html
Roll a die once. Then roll it as many times as the outcome from the first roll.
Getting the special number "3" on any roll means a win.
What is the expected number of wins from this experiment?
1177712
A box has 3 red and 4 black balls. You randomly take one ball at a time without putting it back in.
Stop as soon as all the black balls are drawn out of the box. How many red balls do you expect to be left in the box?
(Hint: find the expected value of the properly defined random variable)
1209827
https://www.algebra.com/algebra/homework/Sequences-and-series/Sequences-and-series.faq.question.1209827.html
Find a closed form for S_n = 1!*(1^2 + 1) + 2!*(2^2 + 2) + . . . + n!*(n^2 + n)
for any integer n >= 1.
1209826
https://www.algebra.com/algebra/homework/Sequences-and-series/Sequences-and-series.faq.question.1209826.html
S_k = 1*(1^2) + 2!*(2^2)*3 + . . . + k*k!*(k + 1).
Find a closed form for S_k.
1173952
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1173952.html
A spheroid (or oblate spheroid) is a surface obtained by rotating an ellipse around its minor axis the ball
in figure 1.41 is in the shape of the lower half of a spheroid that is its horizontal cross-section as circles
well its vertical cross-section that pass through the center a semi-ellipse s if this bowl is 10 inch wide
at the opening and square root 10 in deep at the center how deep does a circular cover with diameter 9 in go into the bowl
1174226 <<<---=== what is presented by @CPhill as "the solution", is a complete gibberish.
https://www.algebra.com/algebra/homework/Average/Average.faq.question.1174226.html
A ladder 4m long at a construction site is resting against a wall. The bottom of the ladder is slipping away from the wall.
Find the estimate of the instantaneous rate of change of the Height H of the top of the ladder with respect to the Distance D
of the bottom of the ladder from the wall when the bottom of the ladder is 2.5m away from the wall.
Use h = 0.01 as the central interval.
1209832 (100)
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1209832.html
A body of weight 500N rests on a plane inclined at 20o to the horizontal. The coefficient of friction
is 0.4, determine a force F at an angle of 15o to the plane required to
(a) Pull the body upwards
(b) Push the body downwards
(c) Pull the body downwards
(d) Push the body upwards
1173392
In a school, every grade 10 student need to study 7 subjects out of 14. It is given that 4 of them are core subject,
and the rest are optional. How many arrangements of the subjects are available for the students?
1172965
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1172965.html
A certain household would like to buy a washing machine set payable for 6 months starting at the end of the month.
How much is the cost of the washing machine if the monthly payment amounts to $3000 and interest is 9% compounded semi-annually?
1172947
The Whittier Company needs to produce 40 units of Product A tomorrow. They can produce on either machine X or machine Y or both.
Each unit of Product A when pro cessed on machine X takes 30 minutes of time, while a unit processed on machine Y takes 25 minutes.
It costs the company $2 per minute and $3 per minute respectively to operate machines X and Y.
Tomorrow, machine X has only 10 hours available to produce Product A, while machine Y can be operated as long as desired.
Use the graphical method to deter mine how many hours to schedule on each machine to minimize production costs.
Draw the isocost lines corresponding to production costs of $2,500, $2,700, $3,000, and $3,500.
Which of the isocost lines result in a feasible but suboptimal solution: Which line is both feasible and optimal? Which is not feasible?
117902
In a class of 50 students 24 like football 21 basketball and cricket six like football and basketball 3 like basketball only,
five like all three games, and 14 did not like any of the three games.
1.illustrate this information of Venn diagram
2. Find the number of students who like
A. Football and cricket
B. Exactly one of the game
C. Exactly two of the game.
1172981
https://www.algebra.com/algebra/homework/word/misc/Miscellaneous_Word_Problems.faq.question.1172981.html
The Truth in Lending Law requires all lending institutions to fully disclose interest rates on all loans.
$5000 is loaned for 36 months with monthly payments of $162.50. Determine annual interest rate.
1171791
https://www.algebra.com/algebra/homework/word/finance/Money_Word_Problems.faq.question.1171791.html
a predator requires 21 units of food A 12 units of food B, and 21 units of food C as its average daily consumption.
these requirements are satisfied by feeling on two prey species.
one prey of species A, provides 6,2 and 3 units of food of A,B, and C, respectively.
to capture and digest a prey of species B provides 3,3 and 5 units of A, B and C, respectively.
to capture and digest a prey of species A requires 7 units of energy, on the average.
the corresponding energy.
How many preys of each should the predator capture to meet its food requirement with minimum expenditure?
find the objective function, constraints and max/min value.
1171394
27 % adults favor the use of unmanned drones by police agencies.
Twelve U.S. adults are randomly selected. Find the probability
that the number of U.S. adults who favor the use of unmanned drones by police agencies is
(a) exactly three,
(b) at least four,
(c) less than eight.
(a) P(3)=
1209876
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209876.html
Polynomials-and-rational-expressions/1209876: Find the largest value of x where the plots of
f(x) = - \frac{2x + 5}{x + 3} and g(x) = \frac{12}{x - 1}
1209874
https://www.algebra.com/algebra/homework/Systems-of-equations/Systems-of-equations.faq.question.1209874.html
Let (x,y,z) be the real solution to the system of equations
x + y = \sqrt{4z + 3}
y + z = \sqrt{4x - 1}
z + x = \sqrt{4y + 5}
Find x + y + z.
1171432 (110)
https://www.algebra.com/algebra/homework/logarithm/logarithm.faq.question.1171432.html
#1. Log2(3x-7)+log2(x+2)=log2(x+1) <<<---=== the solution is incorrect.
#2. Log2(3x+1)-log2(2-4x)>log2(5x-2)
1209929
https://www.algebra.com/algebra/homework/word/finance/Money_Word_Problems.faq.question.1209929.amp
The Pireras are planning to go to Europe 4 years from now and have agreed to set aside $180/month for their trip.
If they deposit this money at the en each month into a savings account paying interest at the rate of 3%/year
compounded monthly, how much money will be in their ‘travel fund at the end of the fourth year?
(Round your answer to the nearest cent.)
1209924
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209924.html
Let x_1, x_2, \dots, x_{100} be real numbers. If
x_1 + 2x_2 + \dots + 100x_{100} = 1,
then find the minimum value of x_1/1 + x_2/2 + \dots + x_{100}/100.
1209908
Let w, x, y, and z be positive real numbers. If w + 2x + 3y + 6z = 8 - w^2 - x^2 - y^2 - z^2,
then what is the maximum value of wxyz?
1170818
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1170818.html
A company claims to have invented a device that can measure the momentum of objects inside it with extreme
accuracy. The device fits within a matchbox, and the claimed precision with which it can measure momentum is
δp = ±10^−26kg ms^−1
Explain why the claimed performance cannot possibly be accurate, and estimate the smallest possible size of a
device with such momentum precision, according to laws of quantum physics.
1209937 <<<---=== the problem itself is SELF-CONTRADICTORY non-sensical gibberish
https://www.algebra.com/algebra/homework/Functions/Functions.faq.question.1209937.html
Let f be a function such that
f(xy) + x = xf(y) + f(x) + xy^2
for all real numbers x and y. If f(-1) = 3, then compute f(100).
1209938
https://www.algebra.com/algebra/homework/Functions/Functions.faq.question.1209938.html
Let f be a function such that
f(x) + f(2x + y) + 5xy = f(4x - y) - x^2 + 5xy - 8x + 17y + 1
for all real numbers x and y. Find f(10).
1209952
https://www.algebra.com/algebra/homework/Functions/Functions.faq.question.1209952.html
The function f(n) is defined for all integers n, such that
f(x) + f(y) = f(x + y) - 4xy - 1 + f(x^2) + f(y^2)
for all integers x and y, and f(1) = 1. Find f(n).
1209950
https://www.algebra.com/algebra/homework/Functions/Functions.faq.question.1209950.html
The function f(n) takes the integers to the real numbers such that
f(m + n) + f(m - n) = 2f(m) + 2f(n) + mn
for all integers m and n, and f(1) = 2. Find f(n).
1209949
https://www.algebra.com/algebra/homework/Functions/Functions.faq.question.1209949.html
The function f : \mathbb{R} \rightarrow \mathbb{R} satisfies
f(x)*f(y) - f(xy) = -2x - 6y + 10
for all x, y \in \mathbb{R}. Find f(x).
1209964 (120)
https://www.algebra.com/algebra/homework/Surface-area/Surface-area.faq.question.1209964.html
ACDF is a Parallelogram. DEF is a sector. ABC is a right triangle. Solve for the area of the composite figure.
https://ibb.co/MyW8MZ2P
1209959
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1209959.html
A club buys tickets for 15 seats in a row for a local production and then sends the tickets randomly
to the 15 people who ordered seats. Of these 15 people, 9 are actors and 6 are backstage workers.
Find the probability that:
(a) An actor and backstage worker will receive tickets sitting together.
(b) The actors will be seated together, and the backstage workers will be seated together.
1209960
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1209960.html
55% of all shark attacks are not fatal. Let r be the number of nonfatal attacks out of a random sample of five shark attacks.
(a) What is the probability all five shark attacks are nonfatal?
(b) What is the probability that three or more of the five shark attacks are nonfatal?
(c) What is the expected number of nonfatal shark attacks out of the five?
(d) What is the standard deviation of the r-probability distribution?
1210228
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1210228.html
Find the number of subsets of
S = \{1, 3, 8, 17, 30, 36, 47, 58\},
so that the sum of the elements in the subset is a multiple of 5.
(Note that for the empty subset, we take the sum of the elements as 0.)
1169789
https://www.algebra.com/algebra/homework/Trigonometry-basics/Trigonometry-basics.faq.question.1169789.html
Given a right pyramid ABCDE, on a square base ABCD, with AB = 8 cm, and height EO = 5 cm,
what are the values of the following:
(a) angle EAB
(b) angle β between a slant edge and the plane on the base.
(c) angle θ between a slant face and the plane on the base.
1210155
https://www.algebra.com/algebra/homework/Surface-area/Surface-area.faq.question.1210155.html
ABCE is a Parallelogram. ADEF is a Rhombus. Find the area of the composite figure.
https://ibb.co/Jj2jKPD3
1210151
https://www.algebra.com/algebra/homework/complex/Complex_Numbers.faq.question.1210151.html
In many ways can the letters of "lyltalqdr" be arranged such that no letter remains in its original position?
1168949
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1168949.html
A quilt is made up of strips of cloth, starting with an inner square
surrounded by rectangles to form successively larger squares.
The inner square and all rectangles have a width of 1 foot.
Write an expression using summation notation that gives the sum of
the areas of all the strips of cloth used to make the quilt shown.
Then evaluate the expression.
1168977
https://www.algebra.com/algebra/homework/Quadratic-relations-and-conic-sections/Quadratic-relations-and-conic-sections.faq.question.1168977.html
Conjugate axis along the y-axis, ome vertex at (0,7), asymptotes are 6x-5y+30=0 and 6x+5y-30=0.
Need help finding the Equation of this hyperbola. How?
1169051
https://www.algebra.com/algebra/homework/Sequences-and-series/Sequences-and-series.faq.question.1169051.html
The sample of work produced by lathe is 10000.
a. If the machine doubled this production every 20 minutes, how much will it produce
in one hour?
b. How long will it take the machine to produce 8 million?
1210173 (130)
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1210173.html
Let P be a point chosen uniformly at random inside triangle ABC. Extend ray BP to hit side AC at D.
What is the probability that BD < 4 ?
The sides of triangle ABC are 3, 5, and 7.
1210172
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1210172.html
Given a regular octagon, in how many ways can we color one diagonal red and another diagonal blue so that the two colored diagonals
intersect at an endpoint? Consider rotations and reflections distinct.
1210184
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1210184.html
I can only remember a seven-digit telephone number if the first three digits (the "prefix") are equal to the next
three digits or the last three digits. For example, I can remember 389-3892 and 274-9274.
How many seven-digit telephone numbers can I remember?
(For this problem, a telephone number cannot start with a 0.)
1210183
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1210183.html
In how many ways can we seat 3 pairs of siblings in a row of 10 chairs, so that nobody sits next to their sibling?
(Two chairs will be left empty, of course.)
1168409
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1168409.html
73% of all Americans live in cities with population greater than 100,000 people.
If 35 Americans are randomly selected, find the probability that
a. Exactly 26 of them live in cities with population greater than 100,000 people.
b. At most 26 of them live in cities with population greater than 100,000 people.
c. At least 25 of them live in cities with population greater than 100,000 people.
d. Between 21 and 25 (including 21 and 25) of them live in cities with population greater than 100,000 people.
1210201
https://www.algebra.com/algebra/homework/Length-and-distance/Length-and-distance.faq.question.1210201.html
Let ABCD be a square with side length 1. A laser is located at vertex A, which fires a laser beam at point X on side BC,
such that BX = 2/3. The beam reflects off the sides of the square, until it ends up at another vertex; at this point,
the beam will stop. Find the length of the total path of the laser beam. The diagram is linked below
https://artofproblemsolving.com/texer/zqcbfanp
1210212
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1210212.html
How many positive integers are there whose digits strictly decrease from left to right, and have at most one even digit,
and the sum of the digits is 6?
1210211
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1210211.html
How many positive integers are there whose digits strictly decrease from left to right, and have at most one even digit,
and the sum of the digits is 6?
1210210
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1210210.html
How many positive integers are there whose digits strictly decrease from left to right, and the sum of the digits is 6?
1210204
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1210204.html
Find the number of ways of arranging one A, two Bs, three Cs, and four Ds, so that no two Bs are next to each other,
no two Cs are next to each other, and no two Ds are next to each other.
1209733 (140)
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1209733.html
60% of all violent felons in the prison system are repeat offenders.
If 45 violent felons are randomly selected, find the probability that
a. Exactly 26 of them are repeat offenders.
b. At most 29 of them are repeat offenders.
c. At least 29 of them are repeat offenders.
d. Between 25 and 33 (including 25 and 33) of them are repeat offenders.
1168408
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1168408.html
64% of all violent felons in the prison system are repeat offenders.
If 48 violent felons are randomly selected, find the probability that
a. Exactly 28 of them are repeat offenders.
b. At most 30 of them are repeat offenders.
c. At least 32 of them are repeat offenders.
d. Between 28 and 34 (including 28 and 34) of them are repeat offenders.
1168513
https://www.algebra.com/algebra/homework/Systems-of-equations/Systems-of-equations.faq.question.1168513.html
Kent sold his car to Carolyn for $1,000 down and monthly payments of $120.03 at the end of every month
for 3 1/2 years. The interest rate charged is 12%, compounded monthly. What was the selling price of the car?
1210228
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1210228.html
Find the number of subsets of
S = \{1, 3, 8, 17, 30, 36, 47, 58\},
so that the sum of the elements in the subset is a multiple of 5. (Note that for the empty subset, we take the sum of the elements as 0.)
1209711
https://www.algebra.com/algebra/homework/playground/test.faq.question.1209711.html
[x-(1/x)]^(1/x) + [1-(1/x)] ^(1/x) = x
1209827
https://www.algebra.com/algebra/homework/Sequences-and-series/Sequences-and-series.faq.question.1209827.html
Find a closed form for
S_n = 1! \cdot (1^2 + 1) + 2! \cdot (2^2 + 2) + \dots + n! \cdot (n^2 + n).\]
for any integer n \ge 1. Your response should have a factorial.
1209826
https://www.algebra.com/algebra/homework/Sequences-and-series/Sequences-and-series.faq.question.1209826.html
For a positive integer k, let
S_k = 1 \cdot 1! \cdot 2 + 2 \cdot 2! \cdot 3 + \dots + k \cdot k! \cdot (k + 1).
Find a closed form for S_k.
1179819
https://www.algebra.com/algebra/homework/Sequences-and-series/Sequences-and-series.faq.question.1179819.html
Find the present values of the following annuities
i. RM6,000 every year for 8 years at 12% compounded annually
ii. RM800 every month for 2 years 5 months at 5% compounded monthly
1209870
https://www.algebra.com/algebra/homework/Functions/Functions.faq.question.1209870.html
Fill in the blanks.
(a) If f(x) is an even function and g(x) is an even function and h(x) is an even function, then f(x) + g(x) + h(x) is an ___ function.
(b) If f(x) is an odd function and g(x) is an odd function and h(x) is an even function, then f(x)*g(x) + h(x) is an ___ function.
(c) If f(x) is an even function and g(x) is an odd function and h(x) is an odd function, then f(x)*(g(x) + h(x)) is an ___ function.
(d) If f(x) is an odd function and g(x) is an even function and h(x) is an odd function, then f(x)*g(x)*h(x) is an ___ function.
The answer to (d) in the post by @CPhill is incorrect.
1209715
https://www.algebra.com/algebra/homework/Polynomials-and-rational-expressions/Polynomials-and-rational-expressions.faq.question.1209715.html
P(x) be a polynomial of the form
P(x) = 2x^3 + ax^2 - 23x + c,
such that 12 and 7 are roots of P(x). What is the third root?
For the polynomial in part (a), compute the ordered pair (a,c).
1190651 (150)
https://www.algebra.com/algebra/homework/word/finance/Money_Word_Problems.faq.question.1190651.html
What is the future value of an ordinary annuity having daily payments of 50 pesos for 30 days with an rate of 20% compounded daily?
1209897
https://www.algebra.com/algebra/homework/Rational-functions/Rational-functions.faq.question.1209897.html
Let x and y be real numbers satisfying
\frac{x^2y^2 - 1}{2y - 1} = 4x + y.
Find the largest possible value of x.
ikleyn
June 29, 2025
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Certainly! Let's evaluate this double integral by converting it to polar coordinates.
First, we need to understand the region of integration defined by the limits:
$$1 \le x \le 2$$
$$0 \le y \le \sqrt{2x - x^2}$$
The upper limit for $y$ can be rewritten as $y^2 = 2x - x^2$, which leads to $x^2 - 2x + y^2 = 0$. Completing the square for the $x$ terms, we get $(x - 1)^2 + y^2 = 1$. This equation represents a circle with center $(1, 0)$ and radius 1.
The condition $y \ge 0$ restricts us to the upper half of this circle. The limits on $x$, $1 \le x \le 2$, further confine the region to the part of the upper semicircle where $x$ ranges from 1 to 2.
Now, let's convert to polar coordinates using the transformations:
$$x = r \cos \theta$$$$y = r \sin \theta$$$$dy \, dx = r \, dr \, d\theta$$
The equation of the circle $(x - 1)^2 + y^2 = 1$ in polar coordinates becomes:
$$(r \cos \theta - 1)^2 + (r \sin \theta)^2 = 1$$$$r^2 \cos^2 \theta - 2r \cos \theta + 1 + r^2 \sin^2 \theta = 1$$$$r^2 (\cos^2 \theta + \sin^2 \theta) - 2r \cos \theta = 0$$$$r^2 - 2r \cos \theta = 0$$$$r(r - 2 \cos \theta) = 0$$
Since $r \ge 0$, we have $r = 2 \cos \theta$.
To determine the limits for $\theta$, we observe the region of integration. The circle intersects the x-axis at $x=0$ and $x=2$. The part of the circle we are interested in corresponds to angles from $\theta = 0$ (where $x=r$) up to where the circle intersects the y-axis tangentially at $x=1$, which corresponds to $\theta = \frac{\pi}{2}$.
The limits for $r$ will go from $0$ to the boundary of the region, which is given by $r = 2 \cos \theta$.
The integrand $x^2y + y^3$ can be written in polar coordinates as:
$$(r \cos \theta)^2 (r \sin \theta) + (r \sin \theta)^3 = r^3 \cos^2 \theta \sin \theta + r^3 \sin^3 \theta = r^3 \sin \theta (\cos^2 \theta + \sin^2 \theta) = r^3 \sin \theta$$
Now we can set up the double integral in polar coordinates:
$$\int_{0}^{\pi/2} \int_{0}^{2 \cos \theta} (r^3 \sin \theta) \cdot r \, dr \, d\theta = \int_{0}^{\pi/2} \int_{0}^{2 \cos \theta} r^4 \sin \theta \, dr \, d\theta$$
Let's evaluate the inner integral with respect to $r$:
$$\int_{0}^{2 \cos \theta} r^4 \sin \theta \, dr = \sin \theta \left[ \frac{r^5}{5} \right]_{0}^{2 \cos \theta} = \sin \theta \left( \frac{(2 \cos \theta)^5}{5} - 0 \right) = \frac{32}{5} \cos^5 \theta \sin \theta$$
Now, we evaluate the outer integral with respect to $\theta$:
$$\int_{0}^{\pi/2} \frac{32}{5} \cos^5 \theta \sin \theta \, d\theta$$Let $u = \cos \theta$, then $du = -\sin \theta \, d\theta$. When $\theta = 0$, $u = 1$, and when $\theta = \pi/2$, $u = 0$.$$\frac{32}{5} \int_{1}^{0} u^5 (-du) = \frac{32}{5} \int_{0}^{1} u^5 \, du = \frac{32}{5} \left[ \frac{u^6}{6} \right]_{0}^{1} = \frac{32}{5} \left( \frac{1^6}{6} - \frac{0^6}{6} \right) = \frac{32}{5} \cdot \frac{1}{6} = \frac{32}{30} = \frac{16}{15}$$
Thus, the value of the double integral is $\frac{16}{15}$.
Final Answer: The final answer is $\boxed{\frac{16}{15}}$
Question 1210338: Determine the perimeter and area:
https://i.ibb.co/ZzVXsg2g/ED907482-977-D-4-DD4-9636-317-CA1-C38-D45.jpg
Found 2 solutions by mccravyedwin, ikleyn:
Answer by mccravyedwin(409)   (Show Source): (Show Source):
Answer by ikleyn(52915)   (Show Source): (Show Source):
Question 1210279: ABFE is a square. EBCD is a kite. Find the area of the composite figure.
https://ibb.co/n8tynFcF
Found 2 solutions by mccravyedwin, greenestamps:
Answer by mccravyedwin(409)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I've been tutoring a high school kid in geometry recently, and discovered
that these days, schools are really stressing special right triangles, using
ratio and proportion between the "standard" special right triangles, and the
right triangles they are given. So I will use that approach entirely.
 The figure is composed of
three 45-45-90 congruent right triangles, BAE, BFE, and BFC.
and
two 30-60-90 congruent right triangles, DFE and DFC
Each 45-45-90 right triangle has hypotenuse 12.
We set up a ratio between the "standard" 45-45-90 right triangle and
the given 45-45-90 right triangle, letting the leg be x:
The figure is composed of
three 45-45-90 congruent right triangles, BAE, BFE, and BFC.
and
two 30-60-90 congruent right triangles, DFE and DFC
Each 45-45-90 right triangle has hypotenuse 12.
We set up a ratio between the "standard" 45-45-90 right triangle and
the given 45-45-90 right triangle, letting the leg be x:




 So the area of each 45-45-90 right triangle is
So the area of each 45-45-90 right triangle is
 Each 30-60-90 right triangle has shorter leg
Each 30-60-90 right triangle has shorter leg 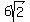 We set up a ratio between the standard 30-60-90 right triangle and
your 30-60-90 right triangles, letting the longer leg be x:
We set up a ratio between the standard 30-60-90 right triangle and
your 30-60-90 right triangles, letting the longer leg be x:




 Since the figure is composed of three 45-45-90 congruent right triangles, and
two 30-60-90 congruent right triangles,
The area of the composite figure is
Since the figure is composed of three 45-45-90 congruent right triangles, and
two 30-60-90 congruent right triangles,
The area of the composite figure is 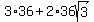 or
or 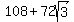 Edwin
Edwin
Answer by greenestamps(13216)   (Show Source): (Show Source):
Question 1210280: A regular hexagon is below. Solve for the area of the hexagon.
https://ibb.co/dsnSzSLK
A watch has the SAME hexagonal face as the picture to the left. If the radius of the circle is 4, then what is the area between the hexagon and circle?
https://ibb.co/ynkmvtbs
Answer by ikleyn(52915)   (Show Source): (Show Source):
Question 1210165: If an isosceles trapezoid CDFG was added below,
where the height was the same as the triangle
above and the bases had a length of 12 and 24,
then what is the area of the new composite figure?
https://ibb.co/jZWQ628k
Answer by ikleyn(52915)   (Show Source): (Show Source):
Question 1210164: If an isosceles trapezoid CDFG was added below,
where the height was the same as the triangle
above and the bases had a length of 12 and 24,
then what is the area of the new composite igure?
https://ibb.co/jZWQ628k
Answer by ikleyn(52915)   (Show Source): (Show Source):
Question 1210167: A regular hexagon is below. Solve for the area of the hexagon.
https://ibb.co/dsnSzSLK
A watch has the SAME hexagonal face as the picture to the left. If the radius of the circle is 4, then what is the area between the hexagon and circle?
https://ibb.co/ynkmvtbs
Found 2 solutions by ArschlochGeometrie, mccravyedwin:
Answer by ArschlochGeometrie(3)  (Show Source): (Show Source):
Answer by mccravyedwin(409)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Sorry, you aren't being careful to state all the information.
You have told us nothing about the size of the hexagon. The hexagon
could be any size. Tell us something about the dimensions of the
hexagon and we'll help you. But there is no way to solve this as given
here. Try to be careful to state everything given.
Edwin
Question 1210166: A regular hexagon is below. Solve for the area of the hexagon.
https://ibb.co/dsnSzSLK
Answer by ikleyn(52915)   (Show Source): (Show Source):
Question 1210163: Solve for the area of the composite figure.
https://ibb.co/cXV52NVm
If an isosceles trapezoid CDFG was added below, where the height was the same as the triangle above and the bases had a length of 12 and 24, then what is the area of the new composite figure?
https://ibb.co/jZWQ628k
Found 3 solutions by mccravyedwin, ArschlochGeometrie, greenestamps:
Answer by mccravyedwin(409)   (Show Source): (Show Source):
Answer by ArschlochGeometrie(3)  (Show Source): (Show Source):
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The figure APPEARS to be a kite plus a triangle. But there is nothing in either your written question or on the referenced figure that tells us so.
We don't even know whether the two segments that APPEAR to be perpendicular to each other in fact are perpendicular.
Without a description of the figure in your text or on the figure, we would only be guessing at the answer.
Re-post, defining the problem clearly.
------------------------------------------------------------------------
Tutor Edwin has solved the problem assuming that the part of the figure that looks like a kite is in fact a kite. Before the trapezoid was added, the area of the composite figure was 132.
When the trapezoid is added, Edwin uses a clever way of finding the area of the trapezoid by dividing it into 3 congruent triangles.
The area of the trapezoid is found more easily using the standard formula for the area of a trapezoid: height times average of the bases. In this problem that is

And then the total area of the new composite figure is 132+144 = 276.
Question 1210155: ABCE is a Parallelogram. ADEF is a Rhombus. Find the area of the composite figure.
https://ibb.co/Jj2jKPD3
Found 4 solutions by ikleyn, mccravyedwin, CPhill, Edwin McCravy:
Answer by ikleyn(52915)   (Show Source): (Show Source):
Answer by mccravyedwin(409)   (Show Source): (Show Source):
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolutely! Let's break down this problem step-by-step.
**1. Finding the area of Rhombus ADEF**
* **Properties of a Rhombus:**
* All sides are equal.
* Diagonals bisect each other at right angles.
* **Given:**
* EF = 17 (side of the rhombus)
* FO = 5 (half of diagonal FD)
* **Finding EO:**
* Since triangle EOF is a right-angled triangle, we can use the Pythagorean theorem: $EF^2 = EO^2 + FO^2$
* $17^2 = EO^2 + 5^2$
* $289 = EO^2 + 25$
* $EO^2 = 289 - 25 = 264$
* $EO = \sqrt{264} = 2\sqrt{66}$
* **Finding Diagonals:**
* FD = 2 * FO = 2 * 5 = 10
* AE = 2 * EO = 2 * $2\sqrt{66}$ = $4\sqrt{66}$
* **Area of Rhombus ADEF:**
* Area = (1/2) * (diagonal 1) * (diagonal 2)
* Area = (1/2) * 10 * $4\sqrt{66}$
* Area = $20\sqrt{66}$
**2. Finding the area of Parallelogram ABCE**
* **Properties of a Parallelogram:**
* Opposite sides are equal and parallel.
* **Given:**
* CD = 11
* EF = 17
* **Finding AE:**
* since ADEF is a rhombus, AE=EF. Therefore AE = 17.
* **Finding the Height of the Parallelogram:**
* The height of the parallelogram is the same as the length EO.
* Height = $2\sqrt{66}$
* **Finding the Area of the Parallelogram:**
* Area = base * height
* Area = AE * EO
* Area = 17 * $2\sqrt{66}$
* Area = $34\sqrt{66}$
**3. Finding the Area of the Composite Figure**
* **Total Area:**
* Area of composite figure = Area of Rhombus ADEF + Area of Parallelogram ABCE
* Total Area = $20\sqrt{66} + 34\sqrt{66}$
* Total Area = $54\sqrt{66}$
**Therefore, the area of the composite figure is $54\sqrt{66}$.**
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
Question 1210156: An envelope is pictured below. Solve for the area of the shaded region.
https://ibb.co/v4zLj1sc
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
Question 1210154: ABCG is a trapezoid.
GCDE is a rhombus.
GEF is half of a kite.
Solve for the area of the composite figure.
https://ibb.co/4RsFBYjz
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
You can put this solution on YOUR website!
My drawing is not quite to scale, because GCDE doesn't quite
look like a rhombus.
I labeled two more points than the drawing on the site, H and I.
 Area of rhombus GCDE is half the product of the diagonals.
Area of rhombus GCDE is half the product of the diagonals.
 Area of triangle EFG is half the base times height
Area of triangle EFG is half the base times height
 Now all we need is the area of trapezoid ABCG.
We must find CG.
The diagonals of a rhombus are perpendicular, and therefore triangle CIG
is a right triangle. GI = DI = 7, and IC = 4, so
Now all we need is the area of trapezoid ABCG.
We must find CG.
The diagonals of a rhombus are perpendicular, and therefore triangle CIG
is a right triangle. GI = DI = 7, and IC = 4, so
 The area of a trapezoid is the average base times the height:
The average base of trapezoid ABCG is
The area of a trapezoid is the average base times the height:
The average base of trapezoid ABCG is  The height of trapezoid is 6, so the area of trapezoid ABCG is
The height of trapezoid is 6, so the area of trapezoid ABCG is
 So we add the three areas together:
Area of trapezoid ABCG =
So we add the three areas together:
Area of trapezoid ABCG =  Area of rhombus GCDE = 56
Area of triangle EFG = 100
Answer =
Area of rhombus GCDE = 56
Area of triangle EFG = 100
Answer = 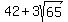  Area of rhombus GCDE is half the product of the diagonals.
Area of rhombus GCDE is half the product of the diagonals.
 Area of triangle EFG is half the base times height
Area of triangle EFG is half the base times height
 Now all we need is the area of trapezoid ABCG.
We must find CG.
The diagonals of a rhombus are perpendicular, and therefore triangle CIG
is a right triangle. GI = DI = 7, and IC = 4, so
Now all we need is the area of trapezoid ABCG.
We must find CG.
The diagonals of a rhombus are perpendicular, and therefore triangle CIG
is a right triangle. GI = DI = 7, and IC = 4, so
 The area of a trapezoid is the average base times the height:
The average base of trapezoid ABCG is
The area of a trapezoid is the average base times the height:
The average base of trapezoid ABCG is  The height of trapezoid is 6, so the area of trapezoid ABCG is
The height of trapezoid is 6, so the area of trapezoid ABCG is
 So we add the three areas together:
Area of trapezoid ABCG =
So we add the three areas together:
Area of trapezoid ABCG = 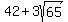 Area of rhombus GCDE = 56
Area of triangle EFG = 100
Answer =
Area of rhombus GCDE = 56
Area of triangle EFG = 100
Answer =  cm2
That's approximately 222.2 cm2
Edwin cm2
That's approximately 222.2 cm2
Edwin
Question 1209972: Find the area of the composite figure. Round your answer to the nearest hundredth.
https://ibb.co/LdtZqqcK
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The figure is composed of an equilateral triangle with side length 10 and a sector of a circle with a radius of 10 and a central angle of 74 degrees.
Area of equilateral triangle with side length x: 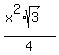
Area of a 74 degree sector of a circle with radius x: 
Use a calculator with x=10 to find the total area and round as directed.
Question 1209968: What is the area of this trapezoid?
https://ibb.co/gZzJPrtd
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
Question 1209969: Find the area of the shaded region.
https://ibb.co/bjxZQDbF
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
You can put this solution on YOUR website!
We want to know the area of the two segments marked "XXX" below
 The triangle is inscribed in a semicircle, i.e., its hypotenuse is a diameter,
so we know it is a right triangle.
Since it has a 30o angle, we know it is a 30-60-90 right triangle.
We know that the longer leg is
The triangle is inscribed in a semicircle, i.e., its hypotenuse is a diameter,
so we know it is a right triangle.
Since it has a 30o angle, we know it is a 30-60-90 right triangle.
We know that the longer leg is  You should learn the following information about the special 30-60-90
special right triangle. It occurs very often.
The sides of the standard 30-60-90 right triangle:
The shorter leg is 1 unit long.
The longer leg is
You should learn the following information about the special 30-60-90
special right triangle. It occurs very often.
The sides of the standard 30-60-90 right triangle:
The shorter leg is 1 unit long.
The longer leg is  units long.
The hypotenuse is 2 units long.
Let the shorter leg of your 30-60-90 right triangle be x.
You are given the longer leg of the 30-60-90 triangle as units long.
The hypotenuse is 2 units long.
Let the shorter leg of your 30-60-90 right triangle be x.
You are given the longer leg of the 30-60-90 triangle as  So make the proportion:
So make the proportion:
  
   cross-multiply:
cross-multiply:
  
  
   So the shorter leg of the 30-60-90 special right triangle is 9 cm.
Therefore the area of the 30-60-90 special right triangle is
So the shorter leg of the 30-60-90 special right triangle is 9 cm.
Therefore the area of the 30-60-90 special right triangle is
 
  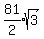 cm2
To get the area of the two segments marked XXX, we must find the radius
of the circle. Since the hypotenuse is twice the shorter side, the
hypotenuse is (9)(2) = 18 cm. The hypotenuse is a diameter, so the radius is
half that or 9.
The area of the whole circle = cm2
To get the area of the two segments marked XXX, we must find the radius
of the circle. Since the hypotenuse is twice the shorter side, the
hypotenuse is (9)(2) = 18 cm. The hypotenuse is a diameter, so the radius is
half that or 9.
The area of the whole circle =  The area of the semicircle the triangle is inscribed in is half that, or
The area of the semicircle the triangle is inscribed in is half that, or
 So we subtract the area of the triangle from the area of the semicircle
and get
So we subtract the area of the triangle from the area of the semicircle
and get
  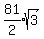 cm2
Factor out cm2
Factor out  , ,
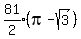 cm2, about 57.1 cm2
Edwin cm2, about 57.1 cm2
Edwin
Question 1209970: Find the area of this figure
https://ibb.co/fG8J40g4
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
Question 1209967: What is the area of this triangle
https://ibb.co/wZnz18XL
Answer by ikleyn(52915)   (Show Source): (Show Source):
Question 1170042: Tank A and Tank B are rectangular prisms and are sitting on a flat table.
Tank A is 10 cm × 8 cm × 6 cm and is sitting on one of its 10 cm × 8 cm faces.
Tank B is 5 cm × 9 cm × 8 cm and is sitting on one of its 5 cm × 9 cm faces.
Initially, Tank A is full of water and Tank B is empty.
The water in Tank A drains out at a constant rate of 4 cm3/s.
Tank B fills with water at a constant rate of 4 cm3/s.
Tank A begins to drain at the same time that Tank B begins to fill.
(i) Determine after how many seconds Tank B will be exactly 1
3
full.
(ii) Determine the depth of the water left in Tank A at the instant when Tank
B is full.
(iii) At one instant, the depth of the water in Tank A is equal to the depth of
the water in Tank B. Determine this depth.
(b) Tank C is a rectangular prism that is 31 cm × 4 cm × 4 cm.
Tank C sits on the flat table on one of its 31 cm × 4 cm faces.
Tank D is in the shape of an inverted square-based pyramid, as shown. It is
supported so that its square base is parallel to the flat table and its fifth vertex
touches the flat table.
The height of Tank D is 10 cm and the side length of its square base is 20 cm.
Initially, Tank C is full of water and Tank D is empty.
Tank D begins filling with water at a rate of 1 cm3/s.
Two seconds after Tank D begins to fill, Tank C begins to drain at a rate of
2 cm3/s.
At one instant, the volume of water in Tank C is equal to the volume of water
in Tank D.
Determine the depth of the water in Tank D at that instant.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem into parts and solve each one.
**(a) Tank A and Tank B:**
**(i) Time for Tank B to be 1/3 full:**
* Volume of Tank B = 5 cm × 9 cm × 8 cm = 360 cm³
* 1/3 of Tank B's volume = 360 cm³ / 3 = 120 cm³
* Tank B fills at 4 cm³/s.
* Time = Volume / Rate = 120 cm³ / 4 cm³/s = 30 seconds.
**(ii) Depth of water in Tank A when Tank B is full:**
* Time to fill Tank B = 360 cm³ / 4 cm³/s = 90 seconds.
* Volume drained from Tank A in 90 seconds = 90 s × 4 cm³/s = 360 cm³.
* Volume of Tank A = 10 cm × 8 cm × 6 cm = 480 cm³.
* Volume remaining in Tank A = 480 cm³ - 360 cm³ = 120 cm³.
* Area of the base of Tank A = 10 cm × 8 cm = 80 cm².
* Depth of water in Tank A = Volume / Area = 120 cm³ / 80 cm² = 1.5 cm.
**(iii) Depth when water depths are equal:**
* Let 't' be the time in seconds.
* Depth of water in Tank B = (4t) / (5 × 9) = 4t / 45 cm.
* Volume of water remaining in Tank A = 480 - 4t cm³.
* Depth of water in Tank A = (480 - 4t) / (10 × 8) = (480 - 4t) / 80 cm.
* Equate the depths: 4t / 45 = (480 - 4t) / 80.
* Cross-multiply: 320t = 45(480 - 4t).
* 320t = 21600 - 180t.
* 500t = 21600.
* t = 21600 / 500 = 43.2 seconds.
* Depth = (4 × 43.2) / 45 = 172.8 / 45 = 3.84 cm.
**(b) Tank C and Tank D:**
* Volume of Tank C = 31 cm × 4 cm × 4 cm = 496 cm³.
* Volume of a pyramid = (1/3) × base area × height.
* Volume of Tank D (when full) = (1/3) × (20 cm)² × 10 cm = 4000/3 cm³.
* Let 't' be the time in seconds after Tank D starts filling.
* Volume of water in Tank D = t cm³.
* Tank C begins draining at t = 2 seconds.
* Volume of water in Tank C at time t = 496 - 2(t - 2) = 500 - 2t cm³.
* We need to find when the volumes are equal:
* t = 500 - 2t
* 3t = 500
* t = 500/3 seconds
* Volume of water in Tank D at this time = 500/3 cm³.
* Volume of water in a square based pyramid when water depth is h is: V = (1/3)*(20*h/10)^2 * h = 4/3*h^3.
* 500/3 = 4/3*h^3
* 500/4 = h^3
* 125= h^3
* h = 5 cm.
**Answers:**
**(a)**
* **(i) 30 seconds**
* **(ii) 1.5 cm**
* **(iii) 3.84 cm**
**(b)**
* **5 cm**
Question 1209964: ACDF is a Parallelogram. DEF is a sector. ABC is a right triangle. Solve for the area of the composite figure.
https://ibb.co/MyW8MZ2P
Found 2 solutions by Edwin McCravy, CPhill:
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Okay, let's break down this problem step-by-step.
**1. Area of the Right Triangle ABC:**
* Since ABC is a right triangle with AB = 4 cm and BC = 4 cm, we can use the formula for the area of a triangle:
* Area = (1/2) * base * height
* Area(ABC) = (1/2) * 4 cm * 4 cm = 8 cm²
**2. Area of the Parallelogram ACDF:**
* We know that AF = 20 cm.
* Since ACDF is a parallelogram, CD = AF = 20 cm.
* To find the area of the parallelogram, we need the base and the height.
* Since the height of the parrallelogram is the same as the length of AB and BC, the height is 4cm.
* Area(ACDF) = base * height
* Area(ACDF) = 20 cm * 4 cm = 80 cm²
**3. Area of the Sector DEF:**
* We are given that angle EDF = 35 degrees.
* We need to find the radius of the sector. Since ACDF is a parallelogram, CD = AF. Also, since ABC is a right triangle with AB = BC, then the length of AC = sqrt(4^2 + 4^2) = sqrt(16+16) = sqrt(32) = 4 * sqrt(2). Because ACDF is a parallelogram, then DE = AC = 4 * sqrt(2) cm. This is the radius of the sector.
* The area of a sector is given by:
* Area = (θ/360°) * π * r²
* Area(DEF) = (35°/360°) * π * (4√2 cm)²
* Area(DEF) = (35/360) * π * 32 cm²
* Area(DEF) = (7/72) * 32π cm²
* Area(DEF) = (224/72)π cm²
* Area(DEF) = (28/9)π cm²
* Area(DEF) ≈ 9.77π cm²
* Area(DEF) ≈ 30.7 cm²
**4. Total Area of the Composite Figure:**
* Total Area = Area(ABC) + Area(ACDF) + Area(DEF)
* Total Area = 8 cm² + 80 cm² + (28/9)π cm²
* Total Area = 88 cm² + (28/9)π cm²
* Total Area ≈ 88 cm² + 30.7 cm²
* Total Area ≈ 118.7 cm²
**Therefore, the total area of the composite figure is approximately 118.7 cm².**
Question 1209963: Find the area of the composite figure if BCEF is a square, BCDG is a trapezoid, and AGB is a sector.
https://ibb.co/gM4Z3rFG
Answer by ikleyn(52915)   (Show Source): (Show Source):
Question 1209961: Find the area of the kite
I got the answer 156.16cm
https://ibb.co/ch1SdtSh
https://ibb.co/gM0Lsps7
Found 3 solutions by mccravyedwin, ikleyn, Edwin McCravy:
Answer by mccravyedwin(409)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Here is a link to a good lesson on the special right triangles:
https://flexbooks.ck12.org/cbook/ck-12-precalculus-concepts-2.0/section/4.3/primary/lesson/special-right-triangles-pcalc/
Edwin
Answer by ikleyn(52915)   (Show Source): (Show Source):
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
Question 1170303: In the cube illustrated, the length of line GH is 34 cm. Point G is the midpoint of line EF, while E and F are midpoints of line AC and line AB respectively. Find the surface area of the cube in cm^3
A) 3092
B) 4050
C) 4136
D) 3218
E) 3264
https://ibb.co/vmkfmPv
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the cube be denoted as ABCDEFGH, where A, B, C, D are the vertices of the bottom face and E, F, G, H are the vertices of the top face.
Let the side length of the cube be $a$.
Given that GH = 34 cm.
Point G is the midpoint of EF.
E is the midpoint of AC.
F is the midpoint of AB.
Let's find the coordinates of the vertices.
Assume the cube is oriented in the first octant with A at the origin (0, 0, 0).
Then the coordinates of the vertices are:
A = (0, 0, 0)
B = (a, 0, 0)
C = (0, a, 0)
D = (0, a, a)
E = (0, a/2, a)
F = (a/2, 0, a)
G = ((a/2 + 0)/2, (0 + a/2)/2, (a + a)/2) = (a/4, a/4, a)
H = (0, a, a)
Now, we are given that GH = 34.
The distance formula between two points $(x_1, y_1, z_1)$ and $(x_2, y_2, z_2)$ is:
$\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}$
GH = $\sqrt{(a/4 - 0)^2 + (a/4 - a)^2 + (a - a)^2}$
34 = $\sqrt{(a/4)^2 + (-3a/4)^2 + 0}$
34 = $\sqrt{a^2/16 + 9a^2/16}$
34 = $\sqrt{10a^2/16}$
34 = $\sqrt{5a^2/8}$
34 = $\frac{a\sqrt{5}}{\sqrt{8}}$
$34\sqrt{8} = a\sqrt{5}$
$a = \frac{34\sqrt{8}}{\sqrt{5}} = \frac{34 \cdot 2\sqrt{2}}{\sqrt{5}} = \frac{68\sqrt{2}}{\sqrt{5}}$
$a^2 = \frac{68^2 \cdot 2}{5} = \frac{4624 \cdot 2}{5} = \frac{9248}{5}$
The surface area of the cube is $6a^2$.
Surface area = $6 \cdot \frac{9248}{5} = \frac{55488}{5} = 11097.6$
However, there is an error in the problem. The correct interpretation should be that G is the midpoint of EF.
Then:
E = (0, a/2, a)
F = (a/2, 0, a)
G = (a/4, a/4, a)
H = (a, a, a)
GH = $\sqrt{(a-a/4)^2 + (a-a/4)^2 + (a-a)^2}$
$34 = \sqrt{(3a/4)^2 + (3a/4)^2 + 0}$
$34 = \sqrt{9a^2/16 + 9a^2/16}$
$34 = \sqrt{18a^2/16}$
$34 = \sqrt{9a^2/8}$
$34 = \frac{3a}{\sqrt{8}}$
$34 = \frac{3a}{2\sqrt{2}}$
$68\sqrt{2} = 3a$
$a = \frac{68\sqrt{2}}{3}$
$a^2 = \frac{68^2 \cdot 2}{9} = \frac{4624 \cdot 2}{9} = \frac{9248}{9}$
Surface area = $6a^2 = 6 \cdot \frac{9248}{9} = \frac{2 \cdot 9248}{3} = \frac{18496}{3} \approx 6165.33$
There is still an error. Let's assume the question meant HG=34, and H is the vertex of the cube, and G is the center of the top face.
H = (a,a,a)
G = (a/2, a/2, a)
$GH = \sqrt{(a-a/2)^2 + (a-a/2)^2 + 0}$
$34 = \sqrt{(a/2)^2 + (a/2)^2} = \sqrt{a^2/4 + a^2/4} = \sqrt{a^2/2}$
$34 = a/\sqrt{2}$
$a = 34\sqrt{2}$
$a^2 = 34^2 \cdot 2 = 1156 \cdot 2 = 2312$
Surface area = $6a^2 = 6 \cdot 2312 = 13872$
Given that H is a vertex of the cube, let's assume G is the center of the top face.
$G = (a/2, a/2, a)$.
$H = (a, a, a)$
$GH = \sqrt{(a/2)^2 + (a/2)^2 + 0} = \sqrt{a^2/2}$
$34 = a/\sqrt{2}$
$a=34\sqrt{2}$
$a^2 = 1156\cdot 2 = 2312$
Surface area = $6\cdot a^2 = 6 \cdot 2312 = 13872$
None of the answers match.
Final Answer: The final answer is $\boxed{13872}$
Question 1170768: A regular pentagonal pyramid has an altitude of 20 cm and a slant height which measures 25cm. Find the base and the lateral areas of the pyramid.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step by step to find the base and lateral areas of the pentagonal pyramid.
**1. Understand the Geometry**
* **Regular Pentagonal Pyramid:**
* Base is a regular pentagon (all sides and angles equal).
* Altitude (height) is the perpendicular distance from the apex to the center of the base.
* Slant height is the altitude of a lateral face (a triangle).
**2. Visualize the Right Triangle**
Imagine a right triangle formed by:
* The altitude (20 cm)
* The slant height (25 cm)
* The apothem (a) of the pentagon (distance from the center of the pentagon to the midpoint of a side).
Using the Pythagorean theorem:
* a² + altitude² = slant height²
* a² + 20² = 25²
* a² + 400 = 625
* a² = 225
* a = √225 = 15 cm
**3. Find the Side Length of the Pentagon (s)**
* Let's consider a right triangle formed by:
* The apothem (a = 15 cm)
* Half of a side (s/2)
* The radius (r) of the pentagon.
* The central angle of a regular pentagon is 360° / 5 = 72°.
* The angle formed by the apothem and the radius is half of the central angle, which is 36°.
* Using trigonometry (tangent):
* tan(36°) = (s/2) / a
* s/2 = a * tan(36°)
* s/2 = 15 * tan(36°)
* s/2 ≈ 15 * 0.7265
* s/2 ≈ 10.8975
* s ≈ 21.795 cm
**4. Find the Base Area (B)**
* Area of a regular pentagon:
* B = (1/2) * apothem * perimeter
* Perimeter (P) = 5 * side length
* P = 5 * 21.795 ≈ 108.975 cm
* B = (1/2) * 15 cm * 108.975 cm
* B ≈ 817.3125 cm²
**5. Find the Lateral Area (LA)**
* Lateral Area = (1/2) * perimeter * slant height
* LA = (1/2) * 108.975 cm * 25 cm
* LA ≈ 1362.1875 cm²
**Rounded Values:**
* Base Area (B) ≈ 817.31 cm²
* Lateral Area (LA) ≈ 1362.19 cm²
**Final Answers:**
* **Base Area:** Approximately 817.31 cm²
* **Lateral Area:** Approximately 1362.19 cm²
Question 1178894: compressair company provides cylindrical tanks of compressed air for divers. There standard tank is a cylinder with a volume of 0.015 m^3. Each cylinder is 75cm long and is designed to fit into a special diver's pack.
a) what is the diameter of the cylinder, to the nearest centimetre
b) compressair staff are designing a new cylinder that also has a volume of 0.015 m^3, but uses less material to make. What are the dimensions of the new cylinder, to the nearest tenth of a centimetre? What is the surface area, to the nearest square centimetre?
c)compressair plans to ship 20 of its standard 75-cm-long cylinders upright in a closed rectangular reinforced cardboard box. Staff are considering packing the cylinders in identical rows or in staggered rows, as shown below. Which packing arrangement will require the box of least volume and surface area
box a: identical 5 on the top 4 going down
box b: staggered 5 on the top 4 going down
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
compressair company provides cylindrical tanks of compressed air for divers.
There standard tank is a cylinder with a volume of 0.015 m^3.
Each cylinder is 75cm long and is designed to fit into a special diver's pack.
a) what is the diameter of the cylinder, to the nearest centimetre
b) compressair staff are designing a new cylinder that also has a volume of 0.015 m^3,
but uses less material to make. What are the dimensions of the new cylinder,
to the nearest tenth of a centimetre? What is the surface area, to the nearest square centimetre?
c)compressair plans to ship 20 of its standard 75-cm-long cylinders upright
in a closed rectangular reinforced cardboard box. Staff are considering packing
the cylinders in identical rows or in staggered rows, as shown below.
Which packing arrangement will require the box of least volume and surface area
box a: identical 5 on the top 4 going down
box b: staggered 5 on the top 4 going down
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
First, nothing is shown below.
Second, part (c) of this problem looks like a JOKE or a TRAP.
Why did I say it ?
Because the scheme 5 + 4 + 5 + 4 allows packing only 5 + 4 + 5 + 4 = 18 cylinders,
and 2 cylinders of 20 remain unpacked.
So, EITHER the problem formulation is skew and curved OR the solution in the post by @CPhill is incorrect.
Thank you for making me smiling !
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's solve this problem step-by-step:
**a) Diameter of the Standard Cylinder:**
1. **Volume Formula:** The volume of a cylinder is V = πr²h, where V is volume, r is radius, and h is height (length).
2. **Given Values:**
* V = 0.015 m³
* h = 75 cm = 0.75 m (convert to meters for consistent units)
3. **Solve for Radius (r):**
* 0.015 = πr²(0.75)
* r² = 0.015 / (0.75π)
* r² ≈ 0.0063661977
* r ≈ √0.0063661977 ≈ 0.079788 m
4. **Convert Radius to Centimeters:**
* r ≈ 0.079788 m * 100 cm/m ≈ 7.9788 cm
5. **Calculate Diameter (d):**
* d = 2r ≈ 2 * 7.9788 cm ≈ 15.9576 cm
6. **Round to Nearest Centimeter:**
* d ≈ 16 cm
**Therefore, the diameter of the standard cylinder is approximately 16 cm.**
**b) Dimensions of the New Cylinder (Less Material):**
To minimize material, we want to minimize the surface area for a given volume. This occurs when the height of the cylinder is equal to the diameter (h = 2r).
1. **Volume Formula:** V = πr²h
2. **Given Values:**
* V = 0.015 m³
* h = 2r
3. **Substitute h = 2r:**
* 0.015 = πr²(2r)
* 0.015 = 2πr³
* r³ = 0.015 / (2π)
* r³ ≈ 0.002387324
* r ≈ ³√0.002387324 ≈ 0.13365 m
4. **Convert Radius to Centimeters:**
* r ≈ 0.13365 m * 100 cm/m ≈ 13.365 cm
5. **Calculate Height (h):**
* h = 2r ≈ 2 * 13.365 cm ≈ 26.73 cm
6. **Round to Nearest Tenth of a Centimeter:**
* r ≈ 13.4 cm
* h ≈ 26.7 cm
7. **Calculate Surface Area (SA):**
* SA = 2πr² + 2πrh
* SA = 2π(13.365)² + 2π(13.365)(26.73)
* SA ≈ 2π(178.623225) + 2π(357.24645)
* SA ≈ 1122.38 + 2244.75
* SA ≈ 3367.13 cm²
8. **Round to Nearest Square Centimeter:**
* SA ≈ 3367 cm²
**Therefore, the new cylinder dimensions are approximately 13.4 cm radius and 26.7 cm height. The surface area is approximately 3367 cm².**
**c) Packing Arrangement (Least Volume and Surface Area):**
1. **Standard Cylinder Dimensions:**
* Diameter (d) = 16 cm
* Radius (r) = 8 cm
* Height (h) = 75 cm
2. **Box A (Identical Rows):**
* Dimensions:
* Length: 5 * d = 5 * 16 cm = 80 cm
* Width: 4 * d = 4 * 16 cm = 64 cm
* Height: 75 cm
* Volume: 80 cm * 64 cm * 75 cm = 384,000 cm³
3. **Box B (Staggered Rows):**
* Dimensions:
* Length: 5 * d = 80 cm
* Width: d + 3 * (d * √3 / 2) = 16 + 3 * (16 * √3 / 2) ≈ 16 + 41.57 = 57.57 cm
* Height: 75 cm
* Volume: 80 cm * 57.57 cm * 75 cm = 345,420 cm³
**Comparison:**
* **Volume:** Box B (staggered) has a smaller volume (345,420 cm³) compared to Box A (384,000 cm³).
* **Surface Area:** Box B will also have a smaller surface area, as it requires a smaller box overall.
**Conclusion:**
The **staggered packing arrangement (Box B)** will require the box of least volume and surface area.
Question 1181233: https://media.discordapp.net/attachments/723023718497910816/849263656024801311/unknown.png?width=367&height=146
Answer by ikleyn(52915)   (Show Source): (Show Source):
Question 1181242: https://media.discordapp.net/attachments/723023718497910816/849268709738676254/unknown.png?width=427&height=111
Answer by ikleyn(52915)   (Show Source): (Show Source):
Question 1188936: water flows into a tank havingthe form of frustum of a right circular cone. The tank is 4m tall with upper radius of 1.5 m and the lower radius of 1 m.when the water in the tank is 1.2 m deep the surface rises at the rate of 0.012 m/s . Calculate the discharge of water flowing into the tank in m3/s.
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Water flows into a tank having the form of frustum of a right circular cone. The tank is 4 m tall with upper radius of 1.5 m
and the lower radius of 1 m. When the water in the tank is 1.2 m deep, the surface rises at the rate of 0.012 m/s.
Calculate the discharge of water flowing into the tank in m3/s.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I will give a solution here different from that in the post by @CPhill.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Here's how to calculate the discharge of water flowing into the conical frustum tank step by step.
The geometry connections
We have the great cone with the base radius of 1.5 m and the height H m (H is measured from the vertex).
We have the small cone with the base radius of 1 m and the height (H-4) m. This cone is cut out.
Therefore, for the small cone we have this proportion from similarity
 = = 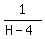 , which gives 1.5H- 1.5*4 = H, 1.5H - H = 6, 0.5H = 6, H = 6/0.5 = 12.
So, the great cone has the height H = 12 m; the small cone has the height 12-4 = 8 m,
and for every current h from vertex and r we have , which gives 1.5H- 1.5*4 = H, 1.5H - H = 6, 0.5H = 6, H = 6/0.5 = 12.
So, the great cone has the height H = 12 m; the small cone has the height 12-4 = 8 m,
and for every current h from vertex and r we have
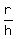 = = 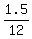 = =  = 0.125.
Therefore, for any current h and r, r = 0.125h, where h is measured from the vertex.
In particular, when r = 1 m (the lower radius), h = 12-4 = 8 meters from the cone vertex.
When the height of the water in the tank is 1.2 meters, h = 8 + 1.2 = 9.2 meters and r = 0.125*(8+1.2) = 1.15 m. = 0.125.
Therefore, for any current h and r, r = 0.125h, where h is measured from the vertex.
In particular, when r = 1 m (the lower radius), h = 12-4 = 8 meters from the cone vertex.
When the height of the water in the tank is 1.2 meters, h = 8 + 1.2 = 9.2 meters and r = 0.125*(8+1.2) = 1.15 m.
The volume of the water in the tank
When the level of the water is h meters from the vertex, the volume of the water is
V = 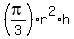 - - 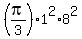 m^3.
Substituting here r = 0.125h, we have this formula for the volume of the water in the tank
V = m^3.
Substituting here r = 0.125h, we have this formula for the volume of the water in the tank
V =  - -  m^3.
We can consider here V and h as functions of time
V(t) = m^3.
We can consider here V and h as functions of time
V(t) =  - - 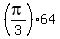 m^3. (1) m^3. (1)
Differentiate the volume of the water in the tank
Write the derivative of the volume of the water in the tank in respect to the time.
The constant term in formula (1) does not matter, so forget about it.
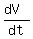 = =  ,
Apply it for h = 8+1.2 = 9.2 meters. It will give ,
Apply it for h = 8+1.2 = 9.2 meters. It will give
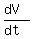 = = 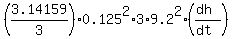 = = 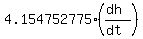 Now substitute the given value of the rate of the surface rise
Now substitute the given value of the rate of the surface rise 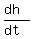 = 0.012 m/s. You will get this equation = 0.012 m/s. You will get this equation
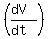 = =  = 0.049857 (rounded).
ANSWER. The inflow rate into the tank is about 0.049857 m^3/s. = 0.049857 (rounded).
ANSWER. The inflow rate into the tank is about 0.049857 m^3/s.
Solved.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to calculate the discharge of water flowing into the tank:
**1. Find the radius of the water surface:**
* We can use similar triangles to relate the radius of the water surface (r) to the depth of the water (h).
* The ratio of the radii is equal to the ratio of the heights:
(r - 1) / (1.5 - 1) = h / 4
r - 1 = 0.5h / 4
r = 1 + 0.125h
* When h = 1.2 m:
r = 1 + 0.125 * 1.2 = 1.15 m
**2. Calculate the cross-sectional area of the water surface:**
* A = πr²
* A = π * (1.15)² ≈ 4.1548 m²
**3. Calculate the discharge (dV/dt):**
* The discharge is the rate of change of volume (dV/dt), which is equal to the cross-sectional area (A) times the rate of change of the water depth (dh/dt).
* dV/dt = A * dh/dt
* dV/dt = 4.1548 m² * 0.012 m/s
* dV/dt ≈ 0.049857 m³/s
**Answer:**
The discharge of water flowing into the tank is approximately 0.049857 m³/s.
Question 1209484: (23) Trapezoid ABCD has diagonals that cross at E. The area of triangle EDC is n². If AB has length m and DC has length n, find the area of trapezoid ABCD in terms of m and n.
Diagram: https://ibb.co/svwxc0w
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! To find the area of trapezoid \( ABCD \), let’s analyze the problem:
### Step 1: Divide the trapezoid into triangles
The diagonals of the trapezoid intersect at point \( E \), dividing it into four triangles: \( \triangle ABE \), \( \triangle CDE \), \( \triangle ADE \), and \( \triangle BCE \).
The given:
- The area of \( \triangle CDE \) is \( n^2 \).
- The bases of the trapezoid are \( AB = m \) and \( DC = n \).
### Step 2: Property of the diagonals
In a trapezoid, the diagonals divide each other proportionally. Let the ratio of the division of each diagonal at \( E \) be \( k : 1 \), where \( k \) is the ratio of the bases:
\[
k = \frac{AB}{DC} = \frac{m}{n}.
\]
### Step 3: Areas of the triangles
The areas of triangles divided by the diagonals are proportional to the lengths of the corresponding bases:
1. Area of \( \triangle EDC \) is \( n^2 \) (given).
2. Area of \( \triangle ABE \) is proportional to \( k^2 \), so:
\[
\text{Area of } \triangle ABE = k^2 \cdot n^2 = \left( \frac{m}{n} \right)^2 \cdot n^2 = m^2.
\]
3. Area of \( \triangle ADE \) and \( \triangle BCE \) are each proportional to \( k \), and their total area equals twice the area of \( \triangle CDE \) (since diagonals divide the trapezoid evenly).
### Step 4: Total area of the trapezoid
The area of trapezoid \( ABCD \) is the sum of the areas of the four triangles:
\[
\text{Area of } ABCD = \text{Area of } \triangle ABE + \text{Area of } \triangle CDE + 2 \cdot \text{Area of } \triangle CDE.
\]
\[
\text{Area of } ABCD = m^2 + n^2 + 2 \cdot n^2.
\]
\[
\text{Area of } ABCD = m^2 + 3n^2.
\]
### Final Answer:
The area of trapezoid \( ABCD \) is:
\[
\boxed{m^2 + 3n^2}.
\]
Question 1209482: Vertices of a regular octagon are connected as shown. What fraction of the octagon is shaded?
Link to graph: https://ibb.co/gFTD6Rg
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Vertices of a regular octagon are connected as shown. What fraction of the octagon  is shaded? is shaded?
Link to graph: https://ibb.co/gFTD6Rg
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let "a" be the side length of this regular octagon.
Then the area of the whole octagon is (3a)^2 - 2a^2 = 9a^2 - 2a^2 = 7a^2.
It is because the area of the square accommodating the octagon is (3a)^2,
from which we should subtract/(cut) four halves of squares with side length "a".
OK. Now, in the picture, we have the shadowed triangle and another, greater triangle,
that accommodates the shadowed triangle.
This greater triangle area is, obviously, 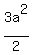 , since this greater triangle is half
of the rectangle with sides "a" and 3a.
Now our goal is to estimate the area of the shadowed triangle.
These two triangles, the shadowed and the greater one, are right-angled triangles with the common
acute angle. So, these two triangles are similar.
To estimate the area of the shadowed triangle, it is enough to find the coefficient of similarity
of the triangles.
Compare the longest legs of these two triangles.
For the greater triangle, the length of its longest leg is 3a.
For the shadowed triangle, the length of its longest leg is the radius of the circumscribed circle
about the regular octagon.
The formula expressing the radius of the circumscribed circle via the side of the regular octagon is
r = , since this greater triangle is half
of the rectangle with sides "a" and 3a.
Now our goal is to estimate the area of the shadowed triangle.
These two triangles, the shadowed and the greater one, are right-angled triangles with the common
acute angle. So, these two triangles are similar.
To estimate the area of the shadowed triangle, it is enough to find the coefficient of similarity
of the triangles.
Compare the longest legs of these two triangles.
For the greater triangle, the length of its longest leg is 3a.
For the shadowed triangle, the length of its longest leg is the radius of the circumscribed circle
about the regular octagon.
The formula expressing the radius of the circumscribed circle via the side of the regular octagon is
r = 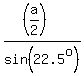 .
So, the similarity coefficient for the two triangles is (as the ratio of the smaller to the larger)
k = .
So, the similarity coefficient for the two triangles is (as the ratio of the smaller to the larger)
k = 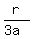 = = 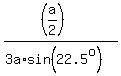 = = 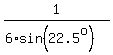 .
Well known fact is that sin(22.5°) = .
Well known fact is that sin(22.5°) = 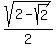 .
Therefore, the similarity coefficient for the two triangles is
k = .
Therefore, the similarity coefficient for the two triangles is
k =  = = 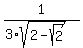 .
Thus the area of the shadowed triangle is
area = .
Thus the area of the shadowed triangle is
area = 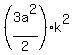 = = 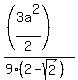 = = 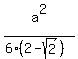 .
To calculate the fraction of the area, we should relate it to 7a^2, the area of the regular octagon.
Thus the ANSWER is: fraction = .
To calculate the fraction of the area, we should relate it to 7a^2, the area of the regular octagon.
Thus the ANSWER is: fraction = 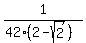 = 0.0406454 (approximately). = 0.0406454 (approximately).
Solved.
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840
|



